Evaluation sur les forces et champs Terminale «D» Cliquer ici
Résumé
NB : Pour plus de détails bien vouloir consulter le cours
On distingue plusieurs types de champ :
Suivant la grandeur étudiée, on a :
• Le champ scalaire, si la grandeur étudiée est un scalaire.
Exemple la température, le pression…
• Le champ vectoriel si la grandeur étudiée est un vecteur.
Exemple: le champ magnétique et électrique
Suivant l’origine du champ, on a ;
• Le champ gravitationnel, son origine étant une particule caractérisée par sa masse; il est mis en évidence par l’attraction universelle
• Le champ électrique, son origine étant une particule chargée, il est mis en évidence par l’attraction coulombienne
• Le champ magnétique son origine étant un aimant
I Interaction gravitationnelle
• Loi de Newton ou loi d’attraction universelle
Énoncé: Deux corps ponctuels A et B, de masses \({m_A}\) et \({m_B}\) exercent l’un sur l’autre des forces d’attraction directement opposées, dirigées suivant la droite (AB), d’intensités proportionnelles à leurs masses et inversement proportionnelles au carré de leur distance.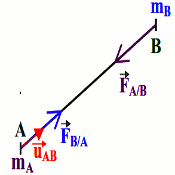 L’expression vectorielle de cette loi est la suivante
L’expression vectorielle de cette loi est la suivante
\({\overrightarrow F _{A/B}} = - G\frac{{{m_A}{m_B}}}{{A{B^2}}}{\overrightarrow u _{AB}}\)
Avec \({\overrightarrow u _{AB}} = \frac{{\overrightarrow {AB} }}{{AB}}\)
Le coefficient de proportionnalité \(G = 6,67 \times {10^{ - 11}}\) N.m2.kg-2 est appelé la constance de gravitation universelle.
Champ de gravitation : C’est la propriété de tout espace à l’intérieur duquel tout corps de masse quelconque est soumis à une force gravitationnelle.
\(\overrightarrow g (A) = - G\frac{{{m_A}}}{{A{B^2}}}{\overrightarrow u _{AB}}\)
L’attraction que la terre exerce sur un corps B placé dans son voisinage décroît avec l’altitude. En effet \(AB = {R_T} + z\) où \({R_T}\) est le rayon de la terre et z l’altitude de B par rapport à la surface de la terre.
\(g(z) = \frac{{G{M_T}}}{{{{({R_T} + z)}^2}}}\) avec \({g_0} = \frac{{G{M_T}}}{{{R_T}^2}}\)
II Interaction électrique.
• Loi de coulomb
Énoncé : La force d’attraction ou de répulsion qui s’exerce entre deux particules A et B de charges électriques \({q_A}\) et \({q_B}\); placées à la distance AB l’une de l’autre, est proportionnelle aux charges \({q_A}\) et \({q_B}\) et est inversement proportionnelle au carré de la distance qui les sépare.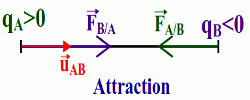 \({\overrightarrow F _{B/A}} = - {\overrightarrow F _{A/B}}\) \( = k\frac{{{q_A}.{q_B}}}{{A{B^2}}}{\overrightarrow u _{_{AB}}}\)
\({\overrightarrow F _{B/A}} = - {\overrightarrow F _{A/B}}\) \( = k\frac{{{q_A}.{q_B}}}{{A{B^2}}}{\overrightarrow u _{_{AB}}}\)
Avec \(k = \frac{1}{{4\pi {\varepsilon _0}}}\) \( = 9 \times {10^9}N.{m^2}{c^{ - 2}}\)
Champ électrique : C’est la propriété de toute région de l’espace à l’intérieur duquel toute charge est soumise à la force de Coulomb.
Il est caractérisé en tout point A de l’espace par le vecteur champ électrique noté \(\overrightarrow {{E_A}} \).
On montre également qu’une charge \({q_A}\) crée en un point B un champ
\(\overrightarrow {{E_A}} = k\frac{{{q_A}}}{{A{B^2}}}{\overrightarrow u _{AB}}\)
III Interaction magnétique
Le champ magnétique est toute région de l’espace à l’intérieur de laquelle une aiguille aimantée est soumise à des forces magnétiques. Il est définie en un point A par son vecteur induction magnétique noté \(\overrightarrow B (A)\) dont les caractéristiques sont les suivantes:
• Point d’application: le point A
• Direction : celle de l’aiguille aimantée placée en ce point.
• Sens: dirigé du pôle sud vers le pôle nord
• Intensité : exprimé en Tesla (T), est mesuré par un tesla mètre
On appelle ligne de champ magnétique la courbe orientée en chaque point de laquelle le vecteur champ magnétique est tangent.
Le spectre magnétique est l’ensemble des lignes de champ magnétique.
Interaction d’un champ magnétique avec un courant électrique
• Loi de Laplace
Énoncè: Une portion de conducteur de longueur l, parcourue par un courant d’intensité I et placée dans un champ magnétique \(\overrightarrow B \), est soumise à une force \(\overrightarrow F \) dite de Laplace appliquée au milieu de la portion et donnée par la relation
\(\overrightarrow F = \overrightarrow {Il} \wedge \overrightarrow B \)
Interaction entre un champ magnétique et une charge électrique
• La loi de Lorentz
Énoncé
Une particule de charge q en mouvement avec une vitesse \(\overrightarrow v \) dans un champ magnétique \(\overrightarrow B \) est soumise à la force magnétique \(\overrightarrow F \) appelée force de Lorentz
\(\overrightarrow F = q\overrightarrow v \wedge \overrightarrow B \)
Evaluation sur les forces et champs Terminale «D» Cliquer ici


