Première
C & E & D & TI
Physique
Correction exercice
Bonjour ! Notre page Facebook, la suivre pour nos prochaines publications
Contenu 1
Énergie potentielle de pesanteur, élastique et de torsion.
Exercice 1
L'énergie mécanique du système solide-ressort horizontal est égale à la somme de l'énergie cinétique du solide et de l'énergie potentielle du ressort :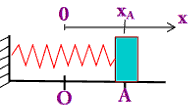
Le solide reste à la même altitude. Par conséquent l'énergie potentielle dans le champ de pesanteur terrestre ne varie pas. Elle est nulle si on choisit l'état de référence à l'altitude où évolue le centre d'inertie du solide.
En l’absence de frottement, l'énergie mécanique du système se conserve.

Le solide reste à la même altitude. Par conséquent l'énergie potentielle dans le champ de pesanteur terrestre ne varie pas. Elle est nulle si on choisit l'état de référence à l'altitude où évolue le centre d'inertie du solide.
En l’absence de frottement, l'énergie mécanique du système se conserve.
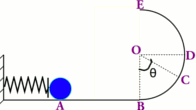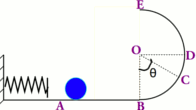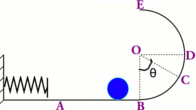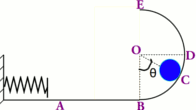
Au point O, \(O\left\{ \begin{array}{l}{x_0} = 0 \Rightarrow {E_{pe}} = \frac{1}{2}k{.0^2} = 0\\{v_0} = v\end{array} \right.\) Au point A \(A\left\{ \begin{array}{l}{x_A} = 4cm \Rightarrow {E_{pe}} = \frac{1}{2}k.x_A^2\\{v_A} = 0\end{array} \right.\)
D’après le principe de conservation de l’énergie mécanique, \({E_m}(A) = {E_m}(O)\) \( \Rightarrow \frac{1}{2}mv_O^2\) \( + \underbrace {\frac{1}{2}k.x_0^2}_0 = \) \(\underbrace {\frac{1}{2}mv_A^2}_0 + \) \(\frac{1}{2}k.x_A^2\)
\(\frac{1}{2}mv_O^2 = \) \(\frac{1}{2}k.x_A^2 \Rightarrow \) \({v_O} = {x_A}\sqrt {\frac{k}{m}} \).
2 Supposons l’énergie potentielle de référence au niveau de la vallée (C) nulle.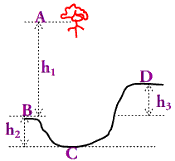
Exprimons la variation de l’énergie potentielle dans les cas suivants:
a- Le niveau de référence est pris au niveau de la vallée.

Exprimons la variation de l’énergie potentielle dans les cas suivants:
a- Le niveau de référence est pris au niveau de la vallée.
Au point A \({E_{PP}}(A) = mg.{z_A}\) \( = mg({h_1} + {h_2})\)
Au point C: \({E_{PP}}(C) = 0\)
\(\Delta {E_{PP}} = {E_{PP}}(C)\) \( - {E_{PP}}(A) = \) \( - mg({h_1} + {h_2})\)
b- Le niveau de référence est pris au niveau de la plaine
Au point A: \({E_{PP}}(A) = \) \(mg.{z_A} = \)\(mg{h_1}\)
Au point C: \({E_{PP}}(C) = - mg{h_2}\)
Au point A: \({E_{PP}}(A) = \) \(mg.{z_A} = \)\(mg{h_1}\)
Au point C: \({E_{PP}}(C) = - mg{h_2}\)
\(\Delta {E_{PP}} = {E_{PP}}(C)\)\( - {E_{PP}}(A) = \)\( - mg({h_1} + {h_2})\)
c- Le niveau de référence est pris au niveau du plateau
Au point A: \({E_{PP}}(A) = \) \(mg.{z_A} = \) \(mg({h_1} - {h_3})\)
Au point C: \({E_{PP}}(C) = \)\( - mg({h_2} + {h_3})\)
Au point C: \({E_{PP}}(C) = \)\( - mg({h_2} + {h_3})\)
\(\Delta {E_{PP}} = {E_{PP}}(C)\)\( - {E_{PP}}(A) = \)\( - mg({h_1} + {h_2})\)
RQ: \(\Delta {E_{PP}} = \) \( - {W_{\overrightarrow {AC} }}(\overrightarrow P ) = \)\( - mg({h_1} + {h_2})\)\( \Rightarrow \) \({W_{\overrightarrow {AC} }}(\overrightarrow P ) = \)\(mg({h_1} + {h_2})\)
Ceci est très juste puisse que le poids est ici une force motrice.
Avant tout calcul d’énergie potentielle, il faut déterminer la constance. Pour cela:
- On choisit un état particulier, dit de référence;
- On attribue une valeur à l’énergie potentielle pour cet état de référence.
L’état de référence et la valeur attribuée sont choisis arbitrairement. Selon ces choix, l’énergie potentielle peut être positive ou négative. Mais la variation d’énergie potentielle entre deux états, seuls quantité mesurable, est indépendance des conventions choisies.
Avant tout calcul d’énergie potentielle, il faut déterminer la constance. Pour cela:
- On choisit un état particulier, dit de référence;
- On attribue une valeur à l’énergie potentielle pour cet état de référence.
L’état de référence et la valeur attribuée sont choisis arbitrairement. Selon ces choix, l’énergie potentielle peut être positive ou négative. Mais la variation d’énergie potentielle entre deux états, seuls quantité mesurable, est indépendance des conventions choisies.
3- La vitesse de la barre étant constante, nous avons , d’après la condition d’équilibre pour les solide en rotation.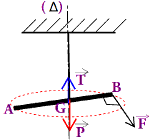

\(\sum {{\mathfrak{M}_\Delta }({{\overrightarrow F }_{EXT}}) = 0} \)\( \Rightarrow {\mathfrak{M}_\Delta }(\overrightarrow P ) + \)\({\mathfrak{M}_\Delta }(\overrightarrow T ) + \)\({\mathfrak{M}_\Delta }(\overrightarrow F ) + \)\({\mathfrak{M}_C} = 0\)
\({\mathfrak{M}_C} = - C\theta \) est le moment du couple de torsion.
\({\mathfrak{M}_\Delta }(\overrightarrow P ) + \)\({\mathfrak{M}_\Delta }(\overrightarrow T ) + \)\({\mathfrak{M}_\Delta }(\overrightarrow F ) + \)\({\mathfrak{M}_C} = 0\)\( \Rightarrow \)\(0 + 0 + F.GB\)\( - C\theta = 0\).
\(\left. \begin{array}{l}2\pi rad \to 1tr\\\theta rad \to 2trs\end{array} \right\}\)\( \Rightarrow \theta = 6\pi rad\) \(C = \frac{{F.l}}{{2\theta }}\)
4- Le niveau de référence est pris au point A et EPP(A)=0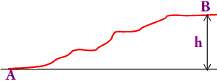
Calcule de la variation d’énergie potentielle:

Calcule de la variation d’énergie potentielle:
\(\left. \begin{array}{l}{E_{PP}}(A) = 0\\{E_{PP}}(B) = mgh\end{array} \right\}\)\( \Rightarrow \Delta {E_{PP}} = mgh\) \(\Delta {E_{pp}} = 14,{1.10^6}J\)
Calcule de la variation d’énergie cinétique:
\(\left. \begin{array}{l}{E_C}(A) = 0\\{E_C}(B) = \frac{1}{2}m.v_B^2\end{array} \right\}\) \( \Rightarrow \) \(\Delta {E_C} = \frac{1}{2}m.v_B^2\). \(\Delta {E_C} = {150.10^6}J\)
Calcule de la variation d’énergie mécanique.
\(\Delta {E_m} = \) \(\Delta {E_C} + \Delta {E_{PP}}\) \( = \frac{1}{2}m.v_B^2\)\( + mgh\) \(\Delta {E_m} = 1,{64.10^8}J\)
Contenu 2
Énergie potentielle de pesanteur.
Exercice I
1 D’après le principe de conservation de l’énergie mécanique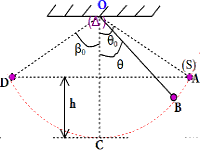

\(E\left( A \right) = E\left( D \right)\)\( \Rightarrow \frac{1}{2}mv_A^2\)\( + mg{z_A} = \)\(\frac{1}{2}mv_D^2 + \)\(mg{z_D}\)
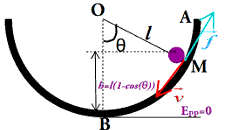
vA= 0 lâchée sans vitesse initiale, vD=0, \(\left\{ {\begin{array}{*{20}{c}}{{z_A} = l\left( {1 - \cos {\theta _0}} \right)}\\{{z_D} = l\left( {1 - \cos {\beta _0}} \right)}\end{array}} \right.\)
\({z_A} = l\left( {1 - \cos {\theta _0}} \right)\)\( = {z_D} = \)\(l\left( {1 - \cos {\beta _0}} \right) \Rightarrow \)\(\cos {\theta _0} = \cos {\beta _0}\) Soit: \({\theta _0} = {\beta _0}\)
On dit que le pendule oscille, lorsqu’il fait des allées et retours autour de OC qui est sa position d’équilibre stable.
2 Évaluons la vitesse du solide au point B.
2 Évaluons la vitesse du solide au point B.
\({E_m}\left( A \right) = {E_m}\left( B \right)\)\( \Rightarrow \frac{1}{2}mv_A^2\)\( + mg{z_A} = \)\(\frac{1}{2}mv_B^2 + mg{z_B}\)
Avec \({v_A} = 0\) , \({z_A} = l\left( {1 - \cos {\theta _0}} \right)\) et \({Z_B} = l\left( {1 - \cos \theta } \right)\) .
\(v_B^2 = \)\(2gl\left( {\cos \theta - \cos {\theta _0}} \right)\)
3 montrons que: \({{\rm{E}}_m}\left( B \right) = \) \(\frac{1}{2}mgl\theta _0^2\)
En effet, \({{\rm{E}}_m}\left( B \right) = \)\(\frac{1}{2}mv_B^2 + \)\(mg{z_B}\) Pour: \(\theta \ll {10^0}\) \(\cos \theta \simeq 1 - \frac{{{\theta ^2}}}{2}\)
\(\left\{ {\begin{array}{*{20}{c}}{{\rm{ }}v_B^2{\rm{ = }}2gl\left( {\cos \theta - \cos {\theta _0}} \right){\rm{ = }}gl\left( {\theta _0^2 - \theta _0^2} \right)}\\{{\rm{ }}{z_B} = l\left( {1 - \cos \theta } \right) = l\frac{{\theta _{}^2}}{2}}\end{array}} \right.{\rm{ }}\)
\({{\rm{E}}_m}\left( B \right) = \)\(\frac{1}{2}mgl\left( {\theta _0^2 - \theta _{}^2} \right)\)\( + mgl\frac{{\theta _{}^2}}{2}\)
\({{\rm{E}}_m}\left( B \right) = \frac{1}{2}mgl\theta _0^2\)
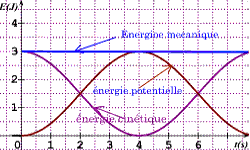
4 À la position d’équilibre stable (verticale passant par O) l’énergie potentielle est nulle et l’énergie cinétique maximale. La courbe qui passe par l’origine est C1. Elle correspond à la courbe de l’énergie potentielle, C2 la courbe de l’énergie cinétique.
5 Traçons la courbe de variation de l’énergie mécanique en fonction du temps (C3). \({E_m} = {E_C} + {E_p}\) \({\rm{ }}{E_m} = 3J{\rm{ }}\) et reste constante
5 Traçons la courbe de variation de l’énergie mécanique en fonction du temps (C3). \({E_m} = {E_C} + {E_p}\) \({\rm{ }}{E_m} = 3J{\rm{ }}\) et reste constante
Contenu 4
Conservation énergie mécanique et pendule de torsion
Exercice I
1. Notons A la position initiale et B la position finale du disque.
1. Notons A la position initiale et B la position finale du disque.
\(A\left\{ \begin{array}{l}{\theta _A} = 2{\rm{ trs}} = 4\pi {\rm{ rads}}\\{\omega _A} = 0{\rm{ rad/s}}\end{array} \right.\) et \(B\left\{ \begin{array}{l}{\theta _B} = 1{\rm{ trs}} = 2\pi {\rm{ rads}}\\{\omega _B} = ?\end{array} \right.\)
D’après la conservation de l’énergie mécanique
\({E_m}(A) = {E_m}(B)\) \( \Rightarrow \)\(\frac{1}{2}{J_\Delta }\omega _A^2 + \frac{1}{2}C\theta _A^2\)\( = \frac{1}{2}{J_\Delta }\omega _B^2 + \frac{1}{2}C\theta _B^2\)
\({\omega _B} = \sqrt {\frac{C}{{{J_\Delta }}}(\theta _A^2 - \theta _B^2)} \) AN: \({\omega _B} = 7,7{\rm{ rad/s}}\)
Lorsque l’angle de torsion est nul, nous avons θB=0 rads/s \({\omega _B} = \sqrt {\frac{C}{{{J_\Delta }}}\theta _A^2} \) AN: \({\omega _B} = 8,86{\rm{ rad/s}}\)