Les erreurs systématiques qui sont généralement liées à l’appareil de mesure et qui se reproduisent à l’identique d’une mesure à l’autre. Si elles sont identifiées, les erreurs systématiques peuvent être éliminées en effectuant la correction adaptée.
L’évaluation des incertitudes par des méthodes systématique est dite évaluation de type B, contrairement à l’incertitude aléatoire qui peut être réduite en augmentant le nombre de mesures, l’incertitude systématique se reproduisent à l’identique d’une mesure à l’autre est estimée à partir de :
• L’étalonnage de l’appareil de mesure (L’étalonnage d’un appareil de mesure est l’opération qui consiste à contrôler ses indications par comparaison avec un autre appareil dit « étalon ».;
• Classe des instruments ;
• Mode d’utilisation de l’appareil ;
• Présence d’autre facteur.
I. Évaluation de l’erreur systématique
Contrairement à l’erreur aléatoire qui se calcule sur une mesure effectuée plusieurs fois, l’erreur systématique est estimée sur une mesure unique.
La mesure est unique lorsqu’elle n’a été faite (ou ne peut être faite) qu’une seule fois
a) Cas d’un appareil de mesure est gradué
L’erreur sur la mesure \(x\), appelée incertitude-type est évaluée dans ce cas si on utilise une règle graduée, un cadran d'un appareil analogique, un thermomètre ...) L'incertitude-type due à la lecture est estimée sur la plus petite graduation. Si nous supposons \(\varepsilon \), la valeur de la plus petite graduation, on peut montrer que :
\(\Delta x = \frac{\varepsilon }{{\sqrt {12} }}\) \( = \frac{\varepsilon }{{2\sqrt 3 }}\)
Ainsi \(x = {x_{lu}} \pm \) \(\frac{\varepsilon }{{2\sqrt 3 }}\)
Pour une incertitude-type élargie : \(\Delta {x_e} = 2\frac{\varepsilon }{{\sqrt {12} }}\) pour \(k=2\)
Exemple En mesurant cet objet, nous obtenons : \(x = {x_{lu}} \pm \) \(\frac{\varepsilon }{{2\sqrt 3 }}\)
En mesurant cet objet, nous obtenons : \(x = {x_{lu}} \pm \) \(\frac{\varepsilon }{{2\sqrt 3 }}\)
\(x = 5,3\) \( \pm \frac{1}{{2\sqrt 3 }}\) \( = 5,3 \pm 0,3\) mm
( la plus petite graduation sur la regle vaut 1 mm soi \(\varepsilon = 1\) mm
b) Cas d’un appareil analogique à déviation possédant une graduation
On classe dans cette catégorie le voltmètre, multimètre … et les caractérise par leur classe de précision. Ainsi connaissant la classe d'un appareil, l’incertitude-type se calcule par la relation
\(\Delta x = \) \(\frac{{classe \times calibre}}{{100\sqrt 3 }}\)
Pour un niveau de confiance de 95%, l’incertitude-type élargie est donnée en multipliant \(\Delta x\) par deux.
c) Dans le cas où l’appareil de mesure est à affichage numérique,
Le constructeur indique pour la précision un pourcentage p de la valeur lue et un nombre N de digits Le terme Digit représente la plus petite valeur non nulle possible affichée par l'appareil lorsqu'il fonctionne sous une gamme (ou calibre) donnée ;
\(\Delta x = \) \(\frac{{p \times valeur\_lue + N\_digits}}{{\sqrt 3 }}\)
Pour un niveau de confiance de 95%, \(k=2\), l’incertitude-type élargie est donnée en multipliant \(\Delta x\) par deux.
Exemple
Un ampèremètre affiche 5,21 mA, la précision est de (3% ± 1 digit)
L'incertitude-type est donnée par :
\(\Delta I = \) \(\frac{{\frac{3}{{100}} \times 5,21 + \frac{1}{{100}}}}{{\sqrt 3 }}\) \( = 0,19 = \) \(0,095 = 0,1\) mA
Pour un niveau de confiance de 95%, \(k=2\), l’incertitude-type élargie est donnée en multipliant \(\Delta I\) par deux.
\(\Delta I = 2 \times 0,1\) \( = 0,2\) mA.
\(I = \) (\(5,2 \pm 0,2\) ) mA.
II. Incertitude type composée
Lors d’un mesurage, la détermination de l’erreur de mesure nécessite de prendre en compte les deux composantes précédentes.
Dans le cas où l’on dispose d’une série de mesures et que chacune d’entre elles est affectée d’une incertitude de type B , on obtient l’incertitude-type composée ( \(\Delta x\)) qui est la somme quadratique de l’incertitude de type A ( \(\Delta {x_A}\) ) et de l’incertitude de type B ( \(\Delta {x_B}\)):
\(\Delta x = \) \(\sqrt {\Delta x_A^2 + \Delta x_B^2} \)
Pour un niveau de confiance de 95%, \(k=2\), l’incertitude-type élargie est donnée en multipliant \(\Delta x\) par deux.
\(\Delta x = \) \(2\sqrt {\Delta x_A^2 + \Delta x_B^2} \)
Ce cours peut être résumé par cette illustration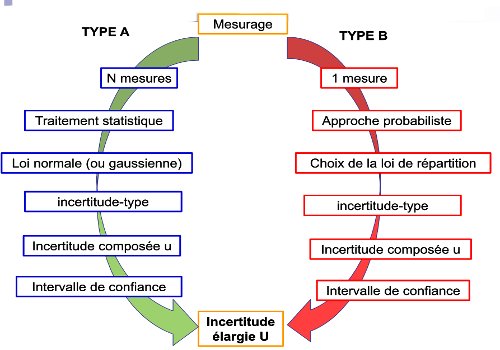
III. Propagation des incertitudes
Lorsque \( x\) se déduit par calcul à partir de \( x\) et \(Z\) connues avec une incertitude-type, la valeur de \(x\) est elle aussi entachée d’incertitude. Le calcul de \(\Delta x\) se fait à partir de \(\Delta y\) et \(\Delta z\).
• si \(x = y – z\) ou \(x = y + z\) alors :
\(\Delta x = \) \(\sqrt {\Delta {y^2} + \Delta {z^2}} \)
• Si \(x = y \times z\) ou \(x = \frac{y}{z}\)
\(\frac{{\Delta x}}{x} = \) \(\sqrt {{{\left( {\frac{{\Delta y}}{y}} \right)}^2} + {{\left( {\frac{{\Delta z}}{z}} \right)}^2}} \)
• Si \(x = {y^n}\)
\(\frac{{\Delta x}}{x} = n\frac{{\Delta y}}{y}\)
Conclusion
Par convention, l’incertitude est arrondie à la valeur supérieure avec au plus deux chiffres significatifs, et les derniers chiffres significatifs conservés pour la valeur mesurée \( x \) sont ceux sur lesquels porte l’incertitude \(\Delta x\).


