Situation de vie :
Lors de la manipulation en classe de troisième sur la lecture de la tension aux bornes d’un dipôle actif, votre petit frère vous rapporte cette image obtenue en filmant l’écran d’un voltmètre.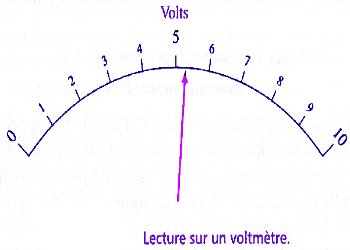
Quelle est la valeur précise de la tension délivrée par ce dipôle ?

Introduction
En sciences expérimentales, il n’existe pas de mesures exactes. Les mesures sont entachées d’erreurs plus ou moins importantes en fonction de la qualité des instruments, de l’habileté du manipulateur.
La mesure ne pouvant être absolument précise, il existe inexorablement un écart entre la valeur obtenue et la valeur exacte (appelée valeur vraie).

I. Notion de mesures
I.1 Définition
La mesure est l’action de déterminer la valeur d’une grandeur par comparaison avec une autre grandeur constante de même espèce prise comme unité (référence).
La mesure d’une grandeur peut se faire par :
a) Comparaison directe
Elle fait appel à une grandeur de référence choisie comme unité
Exemple : Mesure de la masse d’un objet, de la longueur d’un crayon…
b) Comparaison indirecte
Elle exploite un ensemble de propriété plus ou moins simples reliant la grandeur directement mesurable.
Exemple : Pour déterminer le volume du cylindre, on recourt au diamètre et à la hauteur, puis : \[V = \frac{1}{4}\pi {D^2}H\]
c) Comparaison d’effets mesurable
Elle constitue une mesure relative, la détermination d’une force \(\overrightarrow F \) exige que l’on compare l’allongement d’un ressort causé par la force à celui provoqué par la force unité. Le déplacement de l’aiguille le long d’une échelle nous indique la mesure de cette force.
I.2 Qualités d’un appareil de mesure
Trois qualités caractérisent un appareil de mesure
a) La fidélité ;
Il exige que les indications de l’appareil restent invariables avec le temps.
b) La justesse ;
Elle est caractérisée par la plus petite variation de la grandeur à mesurer que l’appareil peut détecter.
c) La sensibilité ;
Elle dépend de l’appareil de mesure utilisée, son intérêt réside essentiellement dans l’élimination des facteurs parasites.

II. Notion d’incertitudes
L'incertitude désigne la marge d'« imprécision » sur la valeur de la mesure d'une grandeur physique.
L’erreur est l’acte de l'esprit d’une personne qui se trompe, qui tient pour vrai ce qui est faux et inversement.
a) Erreur ou incertitude
Les définitions d’erreur et d’incertitudes restent controversées dans le contexte des mesures scientifiques.
L’erreur de mesure d’une grandeur est la différence entre sa valeur mesurée et sa valeur vraie (indiquée par le fabriquant). Notée \(\Delta x\), elle est donnée par la relation : \(\Delta x = \) \({x_{mesure}} - {x_{vrai}}\) et a l’unité de la grandeur mesurée ( \(x\) ).
L’incertitude désigne un intervalle autour de la valeur mesurée, incluant ainsi l’erreur inconnue.
L’intervalle dans lequel il y a une forte probabilité de trouver la valeur « vraie » de la quantité que on mesure est l’incertitude absolue est donnée par : \([{x_{vrai}} - \Delta x,\) \({x_{vrai}} + \Delta x]\)
b) Types d’erreurs
Les erreurs qui faussent couramment les résultats d’une manipulation scientifique sont classées suivant leurs origines en deux groupes :
1) Les erreurs aléatoires ;
Une erreur est aléatoire lorsque, d'une mesure à l'autre, la valeur obtenue peut être surévaluée ou sous-évaluée par rapport à la valeur réelle, elles sont généralement liées à la maladresse du manipulateur et varient d’une mesure à l’autre de manière fortuite.
Ce sont des erreurs d’expérimentation ; (erreur de lecture, de calcul…). Pour les éviter, il faut avoir à priori une idée de certains ordres de grandeur et certaines unités du système international.
2) Les erreurs systématiques
La valeur mesurée est erronée en raison d’une cause spécifique, elles sont généralement liées à l’appareil de mesure.
Exemple de cause : différences propres à chaque instrument (erreurs instrumentales), température et méthode de mesure.
c) Types d’incertitudes
On peut distinguer deux types d’incertitudes :
1) L’incertitude absolue
C’est l’intervalle dans lequel il y a une forte probabilité de trouver la valeur « vraie » de la quantité que on mesure est l’incertitude absolue est donnée par :
\([{x_{vrai}} - \Delta x,\) \({x_{vrai}} + \Delta x]\)
2) L’incertitude relative
C’est un nombre sans dimension noté \(\frac{{\Delta x}}{{\left| x \right|}}\) qui caractérise la précision de la mesure, plus l’incertitude relative est petite, plus la mesure a été précise)
d) Présentation d’un résultat
Présenter le résultat d’une mesure consiste à indiquer la valeur de la grandeur mesurée avec son unité, et préciser l’incertitude de la mesure pour informer de sa précision.
Présentation du résultat d’une mesure : \(X = x \pm \Delta x\)
• \(X\) : grandeur mesurée ;
• \(x\) : valeur de la mesure ;
• \(\Delta x\): incertitude de la mesure ;
• Le dernier chiffre significatif de \(x\) est incertain, il doit être situé à la même position décimale que celui de \(\Delta x\).

III. Calculs des incertitudes
a) Cas d’une mesure unique
La mesure est unique lorsqu’elle n’a été faite (ou ne peut être faite) qu’une seule fois.

• Dans le cas où l’appareil de mesure est gradué, l’incertitude \(\Delta x\) sur la mesure est égale à la moitié de la plus petite graduation de l’appareil.
• Dans le cas où l’appareil de mesure a un affichage numérique, l’incertitude \(\Delta x\) sur la mesure est égale au plus petit écart possible entre deux valeurs mesurées.
• Dans le cas où l’appareil de mesure a un affichage analogique, si la valeur affichée ne se stabilise pas et fluctue entre deux valeurs extrêmes, la valeur accordée à la mesure est la moyenne de ces deux valeurs. L’incertitude \(\Delta x\) est alors égale à la moitié de l’écart entre les deux valeurs extrêmes

b) Cas d’une mesure effectuée plusieurs fois :
Lorsqu’un même opérateur répète plusieurs fois le mesurage de la même grandeur, dans les mêmes conditions expérimentales, il peut trouver des résultats différents. Dans un tel cas, on utilise des notions de statistiques pour analyser les résultats.
La meilleure valeur à retenir pour la grandeur mesurée est la valeur moyenne \(\overline m \) des mesures effectuées.
L’incertitude, appelée dans ce cas « incertitude de répétabilité ») est liée à l’écart-type de la série de mesures, au nombre de mesures n indépendantes et au facteur d’élargissement k (qui dépend du nombre de mesures réalisées et du niveau de confiance choisi).
De manière générale, la répétition des mesures améliore la précision.
Cas d’un phénomène périodique
Dans ce cas, on peut réduire l’incertitude en mesurant la longueur ou la durée de plusieurs périodes.
Exemple : détermination de la période d’un pendule simple.

c) Cas d’une mesure indirecte
Pour une grandeur obtenue par calcul (exemple de la concentration molaire : \(c = \frac{n}{V}\)), l’incertitude (\(\Delta c\)) se calcule à partir des incertitudes des grandeurs utilisées pour le calcul (ici : \({\Delta n}\) et \({\Delta V}\)).
1) Cas du calcul de l’incertitude d’une grandeur \(x\) résultant d’une somme
Si \(x\) résulte d’additions ou de soustractions de grandeurs \({x_1}\) et \({x_2}\) : \(x = n.{x_1}\) \( \pm m.{x_2}\)
L’incertitude de \(x\) est la somme des incertitudes de \(\Delta {x_1}\) et \(\Delta {x_2}\) affectés de leurs coefficients.
\(\Delta x = n.\Delta {x_1}\) \( + m.\Delta {x_2}\)
2) Cas du calcul de l’incertitude d’une grandeur \(x\) résultant d’un produit :
\(x = m.{x_1} \times {x_2}\)
L’incertitude relative est la somme des incertitudes relatives de \(\Delta {x_1}\) et \(\Delta {x_2}\) sans coefficients
\(\frac{{\Delta x}}{x} = \) \(\frac{{\Delta {x_1}}}{{{x_1}}} + \) \(\frac{{\Delta {x_2}}}{{{x_2}}}\)
Soit
\(\Delta x = x\) \(\left[ {\frac{{\Delta {x_1}}}{{{x_1}}} + \frac{{\Delta {x_2}}}{{{x_2}}}} \right]\)

d) Cas d’un instrument dont on connait les caractéristiques :
Dans ce cas, l’évaluation de l’incertitude s’effectue à partir des spécifications du constructeur (tolérance de construction, des propriétés des matériaux constituant l’instrument) et des erreurs de lecture.