I. Quelques définitions

Le mesurage (mesure) : ensemble des opérations permettant de déterminer expérimentalement une ou plusieurs valeurs d’une grandeur.
Le mesurande : c’est la grandeur que l’on veut mesurer (longueur, masse, intensité, résistance, pression…).
La valeur vraie : valeur du mesurande que l’on obtiendrait si le mesurage était parfait. Un mesurage n’étant jamais parfait, cette valeur est toujours inconnue, On parle également de « valeur théorique ».
On appelle dispersion, la tendance qu'ont les valeurs de la distribution d'un caractère à s'étaler, de part et d'autre d'un la médiane, mode ou de la valeur vraie.
Le mot incertitude signifie doute ; l’incertitude du résultat d’un mesurage (mesure) reflète l’impossibilité de connaître exactement la valeur exacte du mesurande.
L’incertitude de mesure est un paramètre, associé au résultat du mesurage, qui caractérise la dispersion des valeurs qui pourraient être raisonnablement attribuées au mesurande.
Il faut donc pouvoir caractériser la dispersion des valeurs que peut prendre la valeur attribuée au mesurande. Une mesure de cette dispersion peut être obtenue à partir de l’écart-type de la grandeur aléatoire.
On peut déterminer la valeur d’une grandeur issue d’une mesure répétée en utilisant un traitement statistique (incertitude aléatoire) ou un traitement systémique (incertitude systémique) ou la combinaison des deux (incertitude composée).
L’erreur aléatoire (erreurs d’appréciation de l’expérimentateur) est à l’origine des incertitudes aléatoires tandis que l’erreur systémique (mauvais étalonnage des instruments de mesure) est à l’origine des incertitudes systémiques.
Prenons par exemple l’expression de l’intensité du poids en fonction de sa masse (m) et l’intensité de la pesanteur (g) : \(P = mg\), si l’incertitude sur la masse et sur son intensité (g) sont connues, nous pouvons avoir accès à l’incertitude sur P par les lois de propagation des incertitude, c.-à-d. par calcul, sinon, connaissant les valeurs répétées de m et g, nous pouvons faire recours à une analyse statistique pour déterminer p et son incertitude.

II. Analyse statistique et Incertitude aléatoire

Toutes les mesures sont sujettes aux incertitudes aléatoires et systémiques, l’analyse statistique des données issues de la mesure aléatoire et répétée d’une grandeur permet de déterminer avec une certaine fiabilité son incertitude.L’évaluation des incertitudes par des méthodes statistiques est dite évaluation de type A (incertitude de répétabilité). Cette évaluation passe par la détermination de la moyenne des quantités mesurées et de l’écart type moyenne qui traduit l’incertitude sur la moyenne.

II.1 Expression de la moyenne

Considérons une grandeur \(x\) uniquement sujette à des incertitudes aléatoires décelables par répétition de mesure \({x_1}\), \({x_2}\), \({x_3}\), …, \({x_N}\)
La moyenne notée \({x_m} = \overline x \) est la meilleure estimation de \(x\) et est donnée par la formule :
\({x_m} = \overline x = \) \(\frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} \)
N représentant le nombre de mesures effectuées.

II.2 Écart-type de la moyenne

L’écart-type moyenne (\({\sigma _{\overline x }}\)) est appelé incertitude-type sur le résultat du mesurage, pour notre grandeur \(x\) définie au paragraphe précèdent, il est donné par la relation :
\[{\sigma _{\overline x }} =k. \frac{{{\sigma _x}}}{{\sqrt N }}\]
Avec \({\sigma _x} = \) \(\sqrt {\frac{1}{{N - 1}}\sum\limits_{I = 1}^N {\left( {{x_i} - \overline x } \right)} } \)
Avec k appelé le niveau de confiance
Ainsi la mesure \(x\) s’écrira
\[x = \overline x \pm {\sigma _{\overline x }}\]

On conclura que l’incertitude a été défini à partir du traitement probabiliste de l’erreur.

II.3 L’intervalle de confiance et niveau de confiance (coefficient de confiance ou facteur d’élargissement)

En mathématiques, un intervalle de confiance encadre une valeur réelle que l’on cherche à estimer à l’aide de mesures prises par un procédé aléatoire.
Un intervalle de confiance doit être associé à un niveau de confiance donnée en pourcentage pour un facteur élargissement notée ( k ) qui n’est rien d’autre que la probabilité (pourcentage) de retrouver la valeur cherchée dans l’intervalle de confiance.
Dans le cas d’une loi de distribution normale :
• Si k = 1, le niveau de confiance est de 68 %,
• Si k = 2, le niveau de confiance est de 95 %,
• Si k = 3, le niveau de confiance est de 99 %,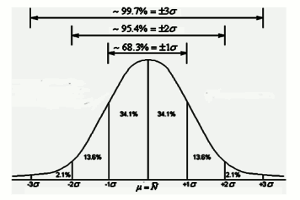
Cet intervalle de confiance sur une mesure x sera donné par :
\(Ic = [\overline x - k{\sigma _{\overline x }}\) \(;\overline x + k{\sigma _{\overline x }}]\)

NB : L’incertitude devient incertitude-type élargie lorsque \(k \succ 1\) ainsi \({\sigma _{\bar x}} = k.\frac{{{\sigma _x}}}{{\sqrt N }}\)

Conclusion

Nous venons de montrer que pour plusieurs mesures aléatoires sur une même grandeur, nous pouvons avoir accès à sa valeur la plus probable en calculant sa moyenne et l’erreur que nous commettons en estimant cette valeur, nous allons montrer dans le cours suivant que pour une seule mesure d’une grandeur, on peut aussi avoir accès à son incertitude qui dans ce cas, appelle incertitude systématique.