Correction exercice I

A) Déterminons les éléments caractéristiques de la similitude directe S dont l’écriture complexe est : \(Z' = \left( {1 - i} \right)\) \(Z + i\)
\(Z’\) est de la forme \(Z' = aZ + b\) avec \(a = 1 - i\) et \(b = i\)
\(a \ne 1\), Soit A le centre S, k le rapport et \(\theta \) son angle.
L’affixe du centre A est \(\frac{b}{{1 - a}}\)1−? ?
\(\frac{b}{{1 - a}} = \) \(\frac{i}{{1 - \left( {1 - i} \right)}}\) \( = 1\)
Le rapport k est tel que : \(k = \left| a \right|\)
\(k = \left| a \right| = \) \(\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \) \( = \sqrt 2 \)
L’angle \(\theta \) est tel que : \(\theta = \arg \left( a \right)\).
Ainsi : \(\left\{ \begin{array}{l}\cos \theta = \frac{{\sqrt 2 }}{2}\\\sin \theta = - \frac{{\sqrt 2 }}{2}\end{array} \right.\) \( \Rightarrow \theta = - \frac{\pi }{4}\)
S est la similitude directe de centre A d’affixe 1, de rapport \({\sqrt 2 }\) et d’angle \( - \frac{\pi }{4}\)
B) Déterminons dans chaque cas, la nature et les éléments caractéristiques de la similitude directe S définie par son écriture complexe :
a) \(Z' = 5Z + 2i\)
a = 5, dans ce cas \(a \in \) \( \mathbb{C}\) \(\backslash \left\{ 1 \right\}\), S est une homothétie de rapport 5.
Déterminons l’affixe \({Z_0}\) de son centre.
\({Z_0} = \frac{{2i}}{{1 - 5}}\) \( = - \frac{1}{2}i\)

Donc S est l’homothétie de centre le point d’affixe \( - \frac{1}{2}i\) et de rapport 5

b) a = 1. Donc, S est la translation de vecteur d'affixe \( - \frac{1}{2}i\)

c) \(a = \frac{1}{2} + i\frac{{\sqrt 3 }}{2}\) dans ce cas \(a \in \) \( \mathbb{C}\) \(\backslash \) \( \mathbb{R}\)
\(\left| {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right| = 1\), donc S est une rotation
Déterminons son angle
\(\arg \left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)\) \( = \frac{\pi }{3}\)
Son angle est donc \(\frac{\pi }{3}\)\(\frac{\pi }{3}\)
Déterminons son centre
\(\frac{b}{{1 - a}} = \) \(\frac{{\frac{1}{2} - i\frac{{\sqrt 3 }}{2}}}{{1 - \left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)}}\) \( = 1\)
Son centre a pour affixe 1.

D'où, S est la rotation de centre le point d'affixe 1 et d'angle \(\frac{\pi }{3}\).

\(a = - 1 + i\), dans ce cas \(a \in \) \( \mathbb{C}\) \(\backslash \) \( \mathbb{R}\)

\(\left| { - 1 + i} \right| = \) \(\sqrt 2 \ne 1\) donc S est une similitude directe \(\arg \left( { - 1 + i} \right)\)
L’angle de S est \(\frac{{3\pi }}{4}\)
\(\frac{b}{{1 - a}} = \) \(\frac{2}{{1 - \left( { - 1 + i} \right)}}\) \( = \frac{4}{5} + \frac{2}{5}i\)

D'où, S est la similitude directe de centre le point\(\frac{4}{5} + \frac{2}{5}i\), de rapport \(\sqrt 2 \) et d'angle \(\frac{{3\pi }}{4}\)

Correction exercice II

A. Déterminons l’écriture complexe de la similitude directe de centre le point A d’affixe \(i\), de rapport \(\sqrt 2 \) et d’angle \(\frac{\pi }{4}\)
La forme générale de l’écriture complexe de S est : \(Z' = k{e^{i\theta }}\) \(\left( {Z - {Z_\Omega }} \right) + {Z_\Omega }\)
Ainsi
\(Z' = \sqrt 2 {e^{i\frac{\pi }{4}}}\) \(\left( {Z - {Z_A}} \right) + {Z_A}\) \( = \sqrt 2 \) \(\left( {\frac{{\sqrt 2 }}{2} + i\frac{{\sqrt 2 }}{2}} \right)\) \(\left( {Z - i} \right) + i\)
\(Z' = \left( {1 + i} \right)\) \(Z + 1\)
Donc l’écriture complexe de S est : \(Z' = \left( {1 + i} \right)\) \(Z + 1\)
B. Écrivons la décomposition canonique de \(s\left( {A;2;\frac{{3\pi }}{2}} \right)\)
\(s\left( {A;2;\frac{{3\pi }}{2}} \right) = \) \(r\left( {A;\frac{{3\pi }}{2}} \right) \circ \) \(h\left( {A;2} \right) = \) \(h\left( {A;2} \right) \circ \) \(r\left( {A;\frac{{3\pi }}{2}} \right)\)
C. Construis l'image \(M'\) d’un point \(M\) par la similitude directe S de centre A, de rapport 3 et d'angle \({\frac{\pi }{6}}\).
\(s\left( {A;3;\frac{\pi }{6}} \right)\) \( = r\left( {A;\frac{\pi }{6}} \right)\) \( \circ h\left( {A;3} \right)\) \( = h\left( {A;3} \right) \circ \) \(r\left( {A;\frac{\pi }{6}} \right)\)
\(s\left( {A;3;\frac{\pi }{6}} \right)\) \( = h\left( {A;3} \right) \circ \) \(r\left( {A;\frac{\pi }{6}} \right)\)
\(\left. M \right|\) \(\overset{r}{\rightarrow}\) \(\left. {{M_1}} \right|\) \(\overset{h}{\rightarrow}\) \(\left. {M'} \right|\)
\(s\left( {A;3;\frac{\pi }{6}} \right) = \) \(h\left( {A;3} \right) \circ \) \(r\left( {A;\frac{\pi }{6}} \right)\)
\(\left. M \right|\) \(\overset{h}{\rightarrow}\) \(\left. {{M_1}} \right|\) \(\overset{r}{\rightarrow}\) \(\left. {M'} \right|\)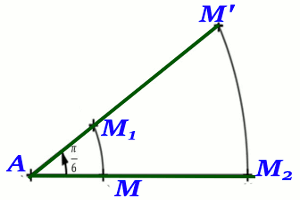

Correction exercice III

Le plan complexe est muni d'un repère orthonormé direct.
On donne les points \(A\left( 2 \right)\), \(B\left( {2 + 2i} \right)\), \(C\left( {1 - 3i} \right)\) et \(C\left( { - 4i} \right)\).
a) Trouve l'écriture complexe de la similitude directe s telle que : \(s\left( A \right) = C\) et \(s\left( B \right) = D\).
Soit \(Z' = aZ + b\), avec \(a \in \) \( \mathbb{C^*}\) et \(b \in \) \( \mathbb{C}\)
\(\left\{ \begin{array}{l}s\left( A \right) = C\\s\left( B \right) = D\end{array} \right.\) \( \Rightarrow \) \(\left\{ \begin{array}{l}a{Z_A} + b = {Z_C}\\a{Z_B} + b = {Z_D}\end{array} \right.\) \( \Rightarrow \) \(\left\{ \begin{array}{l}2a + b = 1 - 3i\\\left( {2 + 2i} \right)a + b = - 4i\end{array} \right.\)
Après resolution du systeme
\(\left\{ \begin{array}{l}a = - \frac{1}{2} + \frac{1}{2}i\\b = 2 - 4i\end{array} \right.\)

L’écriture complexe de s est dont \(Z' = \left( { - \frac{1}{2} + \frac{1}{2}i} \right)\) \(Z + 2 - 4i\)

b) Déterminons les éléments caractéristiques de S.
Notons \(k\) le rapport de S, \(\theta \) son angle et \(\Omega \) son centre :
\(k = \left| { - \frac{1}{2} + \frac{1}{2}i} \right|\) \( = \frac{{\sqrt 2 }}{2}\)
\(\theta = \) \(\arg \left( { - \frac{1}{2} + \frac{1}{2}i} \right)\) \( = \frac{{3\pi }}{4}\)
\({Z_\Omega } = \) \(\frac{{2 - 2i}}{{1 - \left( { - \frac{1}{2} + \frac{1}{2}i} \right)}}\) \( = 2 - 2i\)
Donc, S est la similitude directe de centre \(\Omega \left( {2 - 2i} \right)\), de rapport \(\frac{{\sqrt 2 }}{2}\) et d'angle \(\frac{{3\pi }}{4}\).

Correction exercice IV

Dans le plan muni d'un repère orthonormé direct, on donne les points \(A\left( { - 2 + i} \right)\), \(B\left( {1 + 2i} \right)\) et \(C\left( {2 - i} \right)\). On considère la similitude directe S de centre A telle que : \(s\left( B \right) = C\).
a) Trouvons l'écriture complexe de S.
\(\left\{ \begin{array}{l}s\left( A \right) = A\\s\left( B \right) = C\end{array} \right.\)
Apres résolution de ce système d’équation, nous aurons
\(a = \frac{{ - 4 + 2i}}{{ - 3 - i}}\) et \(b = - 1 - 2i\)
Ainsi : \(Z' = \left( {1 - i} \right)Z\) \( - 1 - 2i\)

b) Déterminons les éléments caractéristiques de S
S a un centre, donc S n’est pas une translation.
\(a = 1 - i\), \(a \in \) \( \mathbb{C}\) \ \( \mathbb{R}\) donc S n’est pas une homothétie.
\(\left| {1 - i} \right| = \sqrt 2 \) \( \ne 1\) donc S n’est pas une rotation.
D’où S est la similitude directe de centre A de rapport \(\sqrt 2 \) et d'angle \(\arg \left( {1 - i} \right)\)
Soit \(\theta \) l’argument principal \(\left( {1 - i} \right)\)
\(\left\{ \begin{array}{l}\cos \theta = \frac{1}{{\sqrt 2 }}\\\sin \theta = - \frac{1}{{\sqrt 2 }}
\end{array} \right.\) \( \Leftrightarrow \theta = - \frac{\pi }{4}\)

Conclusion : S est la similitude directe de centre A, de rapport \(\sqrt 2 \) et d’angle \( - \frac{\pi }{4}\)

Correction exercice V

a) Le rapport de la similitude S est \(\sqrt 2 \). Le triangle OIJ a pour aire \(\frac{1}{2}\) ua.
Donc l’aire \({a_1}\) de l’image du triangle OIJ est :
\({\left( {\sqrt 2 } \right)^2} \times \frac{1}{2}\) \( = 2 \times \frac{1}{2} = 1\) ua, soit 1ua.
b) Soit \(O’\) l’image de \(O\) par S.
On a : \({Z_{O'}} = \) \( - 1 - 2i\).
(\(C_2\) ) est le cercle de \(O’\) et de rayon \(2\sqrt 2 \).
c) Soit \(I’\) l’image de \(I\) par S.
On a : \({Z_{I'}} = - i\). L’image de la droite (OI) par S est la droite (O’I’).