Un nombre complexe peut être écrit sous différentes formes, au-delà de forme algébrique qui s’écrit : Z=a+ib, nous pouvons aussi avoir :
I. Forme trigonométrique d'un nombre complexe
I.1 Définition
Soit Z=a+ib, un nombre complexe de module r et d’argument θ. On appelle forme trigonométrique de Z toute écriture de la forme Z=r (cosθ+isinθ) avec r= √a2+b2 et
θ∈[−π;π[ {cosθ=arsinθ=br
I.2 Propriétés
Soient Z et Z′ deux complexe tels que Z=r (cosθ+isinθ) et Z′=r′ (cosθ′+isinθ′)
P.1 Z×Z′=r×r′ (cos(θ+θ′) +isin(θ+θ′))
P.2 ZZ′=rr′ (cos(θ−θ′)+ isin(θ−θ′))
P.3 Zn=rn (cosnθ+isinnθ)
N.B : si r=1 Zn= (cosnθ+isinnθ)
II. Forme polaire d’un nombre complexe
II.1 Définition :
Soit Z un nombre complexe de module r et d’argument θ, On appelle forme polaire de Z toute écriture de Z de la forme Z=[r;θ]
II.2 Propriétés :
Soient Z et Z′ deux complexe tels que Z=[r;θ] et Z′=[r′;θ′]
P.1 Z×Z′= [r×r′;θ+θ]
P.2 ZZ′= [rr′;θ−θ′]
P.3 Zn= [rn;nθ′]
III. Forme exponentielle d'un nombre complexe
III.1 Définition
Soit Z un nombre complexe de module r et d’argument θ. On appelle forme exponentielle d'un nombre complexe Z, toute écriture de Z se ramenant sous la forme Z=reiθ où son conjugué est 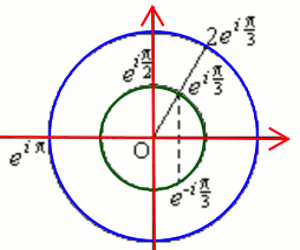¯Z=re−iθ
III.2 Propriétés :
Soient Z et Z′ deux nombres complexes de formes exponentielles respectives : Z=reiθ et Z′=r′eiθ′
P.1 Z×Z′= r×r′ei(θ+θ′)
P.2 ZZ′=rr′ ei(θ−θ′)
P.3 ZׯZ= r×r′ ei(θ−θ)=r2
P.4 Zn=rneinθ
P.5 : Formule d'Euler
{cosθ=eiθ+e−iθ2sinθ=eiθ−e−iθ2 soit {cosnθ=einθ+e−inθ2sinnθ=einθ−e−inθ2
