Correction exercice I
1.1 Les valeurs des tensions maximales :
\({U_{mR}} = 2,5 \times 2 = 5V\)
\({U_m} = 3,5 \times 2 = 7V\)
La période \(T = 8 \times 2,5 \times {10^{ - 3}}\) \( = 2 \times {10^{ - 2}}s\) et \({N_1} = \frac{1}{T} = 50Hz\)
1.2
\({u_R}\) est en avance de phase sur \(u\) car \({u_R}\) passe par son maximum avant \(u(t)\) donc le circuit est capacitif.
Phase de \(i\) par rapport à \(u\) \(\left| \varphi \right| = \omega \Delta t \Rightarrow \) \(\left| \varphi \right| = \frac{\pi }{5}\)
Expression de \({\cos \varphi }\)
\(\cos \varphi = \frac{{R + r}}{Z}\) avec \({Z = \frac{U}{I}}\) soit \(\cos \varphi = \frac{{\left( {R + r} \right)}}{U}I\)
1.3 Calcul des résistances :
\({U_R} = RI \Rightarrow R\) \( = \frac{{{U_R}}}{I} = \frac{{{U_{mR}}}}{{I\sqrt 2 }}\) \( = 60\Omega \)
\(\cos \varphi = \frac{{\left( {R + r} \right)}}{U}I\) \( \Rightarrow r = \frac{U}{I}\cos \varphi \) \( \Rightarrow r = \frac{U}{I}\cos \varphi \)
2 Résonance
\(\overrightarrow {{u_3}} = \overrightarrow {{u_1}} + \overrightarrow {{u_2}} \Rightarrow \) \(U_3^2 = U_1^2 + U_2^2 + \) \(2{U_1}.{U_2}\cos {\varphi _1}(a)\)
De même \({U_3} = {U_1} + {U_2}\) \( \Leftrightarrow U_3^2 = U_1^2 + U_2^2\) \( + 2{U_1}.{U_2}(b)\)
\((a) = (b)\) alors \(\cos {\varphi _1} = 1\) soit \({\varphi _1} = 0\)
d’où \(\overrightarrow {{u_2}} \) est confondue avec \(\overrightarrow {{u_1}} \), ainsi\(\varphi = 0\), le circuit est donc en résonance.
L’ampèremètre indique l’intensité efficace maximale \({I_0}\)
\({I_0} = \frac{{{U_3}}}{{R + r}} = 73mA\)
L’expression de la fréquence \({N_2}\) à la résonance \({N_2} = \frac{1}{{2\pi \sqrt {LC} }}\)
3 Nature du circuit
D’après l’exercice les tensions \(U\), \({U_C}\) et \({U_b}\) sont égales, \(Z = {Z_C} = {Z_b}\)
\({Z_C} = {Z_b} \Leftrightarrow \) \(\frac{1}{{C\omega }} = \sqrt {{r^2} + {{(L\omega )}^2}} \) Soit \({\left( {\frac{1}{{C\omega }}} \right)^2} = {r^2} + {(L\omega )^2}\)
Alors \({\frac{1}{{C\omega }} \succ L\omega }\) donc le circuit est capacitif
\(Z = {Z_C} \Leftrightarrow \) \(\frac{1}{{C\omega }} = \sqrt {{r^2} + {{(L\omega - \frac{1}{{C\omega }})}^2}} \) (1)
\(Z = {Z_b} \Leftrightarrow \) \(\sqrt {{r^2} + {{(L\omega )}^2}} = \) \(\sqrt {{r^2} + {{(L\omega - \frac{1}{{C\omega }})}^2}} \) Soit \( - L\omega = L\omega - \frac{1}{{C\omega }}\) \( \Rightarrow 2L\omega = \frac{1}{{C\omega }}\) (2)
(2) dans (1), on obtient \( - L\omega = L\omega - \) \(\frac{1}{{C\omega }} \Rightarrow {\left( {2L\omega } \right)^2} = {r^2}\) \( + {(L\omega )^2} \Rightarrow L = \) \(\frac{r}{{2\pi {N_3}\sqrt 3 }}\) Soit \(L = 13 \times {10^{ - 3}}H\).
\(C = \frac{1}{{8{\pi ^2}N_3^2L}} = \) \(3 \times {10^{ - 4}}F\)
Calcul de la fréquence à la résonance : \({N_2} = \frac{1}{{2\pi \sqrt {LC} }} = 81Hz\).
Correction exercice II
1 Déterminons la fréquence à la résonance \(N_0\) :
A la résonance l’intensité efficace est maximal soit d’après la courbe \(N_0 =100Hz\).
Déduction de l’inductance : A la résonance : \(LC\omega _0^2 = 1 \Rightarrow L\) \( = \frac{1}{{4{\pi ^2}N_0^2C}} = 0,25H\)
2 La courbe 2 correspond à une résonance floue. La courbe1 correspond à une résonance aigue
3 Calcule du rapport \(\frac{{{R_1}}}{{{R_2}}}\)
\(U = {R_1}{I_{{0_1}}} = \) \({R_2}{I_{{0_2}}} \Rightarrow \frac{{{R_1}}}{{{R_2}}} = \) \(\frac{{{I_{{0_1}}}}}{{{I_{{0_2}}}}} = \frac{1}{2}\)
4.1 Nature du circuit :
Comme \(L{\omega _1} = 0,25 \times 2\) \( \times \pi \times 72 = 36\pi \) et \(\frac{1}{{C{\omega _1}}} = 69,44\pi \), le circuit est capacitif car \(L{\omega _1} \prec \frac{1}{{C{\omega _1}}}\)
Donc \({u_{{R_1}}}\) est en avance de phase sur \(u\) d’où la courbe \(C_2\) correspond à \({u_{{R_1}}}\)
4.2 Le facteur de puissance \(\cos \varphi \) :
D’après les courbes \(\left| \varphi \right| = 2\pi \frac{{\Delta t}}{T}\) \( = 2\pi \frac{1}{6} = \frac{\pi }{3}\)
d’où \({\cos \varphi = \frac{1}{2}}\)
4.3 Calcule de \({R_1}\):
\(\tan \varphi = \frac{{L{\omega _1} - \frac{1}{{C{\omega _1}}}}}{{{R_1}}}\) \( \Rightarrow {R_1} = \frac{{L{\omega _1} - \frac{1}{{C{\omega _1}}}}}{{\tan \varphi }}\) \( = 61\Omega \)
Calcule de \(R_2\) :
\(\frac{{{R_1}}}{{{R_2}}} = \frac{1}{2} \Rightarrow \) \({R_2} = 122\Omega \)
La tension U:
\(U = {R_1}{I_{{0_1}}}\) \( = 36,6V\)
4.4 Le facteur de surtension Q :
\(Q = \frac{{L{\omega _0}}}{{{R_1}}} = 2,6\)
Correction exercice III
1. Le schéma du montage.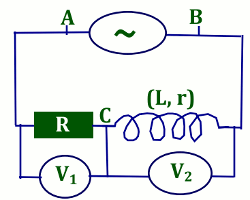 \(U = {U_{AB}} = 110V\)
\(U = {U_{AB}} = 110V\)
\({U_1} = {U_{AC}} = 45,5V\)
\({U_2} = {U_{CB}} = 80V\)
2. Construisons le diagramme de Fresnel relatif à cette expérience représentant les trois tensions \({u_1}\), \({u_1}\) et \(u\).
\(i(t) = {{\mathop{\rm I}\nolimits} _m}\cos (\omega t)\)
\(U = {U_1} + {U_2}\)
\(O{A_1} \to {U_1} = \) \({U_{{m_1}}}\cos (\omega t)\)
\({A_1}{A_2} \to {U_2} = \) \({U_{m2}}\cos (\omega t + {\varphi _2})\)
\(OA \to U = \) \({U_m}\cos (\omega t + \varphi )\)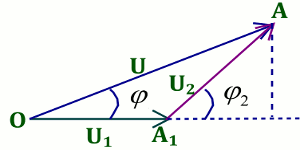 3. Calculons l'impédance de la bobine.
3. Calculons l'impédance de la bobine.
\({Z_2} = \frac{{{U_2}}}{I}\) et \({Z_1} = r = \frac{{{U_1}}}{I}\) soit \({Z_2} = \frac{{{U_2}}}{{{U_1}}}r = 44\Omega \)
4. Déterminons la phase de \({u_2}\) par rapport à \(i\).
\(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overline {{A_1}A} \)
\(O{A^2} = OA_1^2 + {A_1}{A^2} + \) \(2O{A_1}.{A_1}A\cos {\varphi _2}\)
\(\cos {\varphi _2} = \) \(\frac{{{U^2} - U_1^2 - U_2^2}}{{2{U_1}{U_2}}}\) \( = 0,5\)
soit \({\varphi _2} = \frac{\pi }{3}\) rad
5. Calculons les valeurs des grandeurs R et L.
\(\cos {\varphi _2} = \frac{R}{{{Z_2}}} \Rightarrow \) \(R = {Z_2}\cos {\varphi _2}\) \( = 22\Omega \)
\(\tan {\varphi _2} = \frac{{L\omega }}{R} \Rightarrow \) \(L = \frac{{R\tan {\varphi _2}}}{{2\pi N}} = 0,12H\)
6. Calculons la puissance moyenne consommée dans le circuit.
\(P = (r + R){I^2} = \) \(\frac{{(r + R)U_1^2}}{{{r^2}}} = 155,68W\)

