Correction exercice I

1. La probabilité d’apparition des faces (1, 2, 3, 4, 5, 6) étant la même, alors \(P(X = 1) = P(X = 2)\) \( = P(X = 3) = P(X = 4)\) \( = P(X = 5) = \) \(P(X = 6) = \frac{1}{6}\).
\(E(X) = 1 \times \frac{1}{6} + 2 \times \frac{1}{6}\) \( + ... + 6 \times \frac{1}{6} = \frac{7}{2}\).
2. Soit X le nombre de piles « donc de succès » au total.
X est une variable aléatoire binomiale de paramètres (n = 5, \(p = \frac{1}{2}\))
\(P(X = {x_i}) = \) \(C_5^i{\left( {\frac{1}{2}} \right)^i}{\left( {1 - \frac{1}{2}} \right)^{5 - i}}\)
\(X = 0\) veut dire qu’après avoir lancé à la fois les 5 pièces, nous n’avons aucune face « pile »
\(P(X = 0) = \) \(C_5^0{\left( {\frac{1}{2}} \right)^0}{\left( {1 - \frac{1}{2}} \right)^5}\) \( = \frac{1}{{32}}\) \( = P(X = 5)\)
\(X = 1\) veut dire qu’après avoir lancé à la fois les 5 pièces, nous n’avons une face « pile »
\(P(X = 1) = \) \(C_5^1{\left( {\frac{1}{2}} \right)^1}{\left( {\frac{1}{2}} \right)^1} = \frac{5}{{32}}\) \( = P(X = 4)\)
\(P(X = 2) = \) \(P(X = 3) = \frac{{10}}{{32}}\)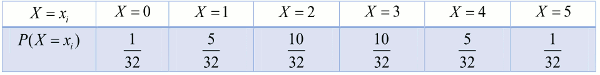

Correction exercice II

1. En supposant que les dés soient pas truqués et que leurs résultats soient indépendants les uns des autres. Le nombre de fois qu'apparaît le nombre sur lequel le joueur a misé est une variable aléatoire binomiale de paramètres (3, \(\frac{1}{6}\)).
Désignons par X les gains du joueur lors d'une partie. On aura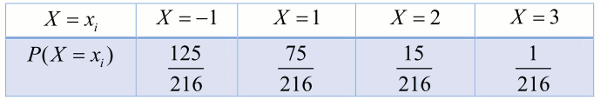
2. Calculons l’espérance mathématique, en effet :
\(E(x) = \) \(\frac{{ - 125 + 75 + 30 + 3}}{{216}}\) \( = \frac{{ - 17}}{{216}}\)
Ainsi, sur un nombre infini de parties, le joueur perdra 17 unités par groupe de 216 parties. Le jeu n’est pas honnête pour le jouer.

Correction exercice III

On pose X la variable aléatoire représentant le nombre de blocs tombés en panne. Les différentes valeurs de X sont les suivantes:
• \({x_1} = 0\) : aucun bloc n'est tombé en panne ;
• \({x_2} = 1\) : un bloc est tombé en panne ;
• \({x_3} = 2\) : deux blocs sont tombés en panne ;
• \({x_4} = 3\) : trois blocs sont tombés en panne.
On rappelle la loi de Bernoulli : \({P_n}(X = k) = C_n^k\) \({\left( p \right)^k}{\left( {1 - p} \right)^{n - k}}\), ainsi, nous avons \(p = 0,10\), \(\overline p = 1,00 - 0,10 = 0,90\), \(n = 3\)

Correction exercice IV

X variable aléatoire représentant le nombre d’œufs de bonne qualité parmi les choisis dont les valeurs sont \({x_1} = 0\), \({x_2} = 1\), \({x_3} = 2\), ce qui représente 0, 1; 2 œufs bonne qualité choisis.
Le nombre total de choix de 2 œufs parmi 10 est égal au nombre de combinaisons de 10 œufs par 2.
En supposant \(k\) le nombre d'œufs de bonne qualité parmi les deux choisis, on pose alors on choisira \(k\) œufs parmi \(n = 8\) œufs de bonne qualité, par conséquent le nombre de combinaisons possibles de \(k\) œufs parmi \(n\) est \(C_n^k\), ainsi, on dira que \(m – k\) œufs ne sont pas de bonne qualité; ce qui donne \(C_{10 - n}^{2 - k}\) combinaisons. Il vient alors que le nombre de cas favorables est donné par la formule \(C_n^kC_{10 - n}^{2 - k}\) d'où la probabilité suivante : \(P(X = k) = \) \(\frac{{C_n^kC_{10 - n}^{2 - k}}}{{C_{10}^2}}\)
• \(P(X = 0) = \) \(\frac{{C_8^0C_{10 - 8}^{2 - 0}}}{{C_{10}^2}} = \) \(\frac{{C_8^0C_2^2}}{{C_{10}^2}} = \frac{1}{{45}}\)
• \(P(X = 1) = \) \(\frac{{C_8^1C_2^1}}{{C_{10}^2}} = \frac{{16}}{{45}}\)
• \(P(X = 2) = \) \(\frac{{C_8^2C_2^0}}{{C_{10}^2}} = \frac{{28}}{{45}}\)
À partir d’ici, vous pouvez établir la loi de répartition

Correction exercice V.

1. L’examinateur peut poser i : 2; ..., m. questions à ce candidat, donc les différentes valeurs que peut prendre la variable aléatoire discrète X sont : 1 ; 2;...; m;...
Déterminons les probabilités correspondantes à chacune de ces valeurs; soit \(P(X = k)\).
• Pour \(X = 1\), c'est-à-dire que le candidat ne connaît pas la réponse à la première question posée,
\(P(X = 1) = \) \(1 - p = 1 - 0,90\) \( = 0,10\)
où \(p\) est la probabilité qu'il réponde à une question
• Pour \(X = 2\), c'est-à-dire que le candidat a répondu à la première question et pas à la deuxième question posée ;
\(P(X = 2) = 0,10\) \( \times 0,90 = 0,09\)
(visitons le cours sur les théories de probabilités)
…
Pour \(X = m\), c'est-à-dire que le candidat a répondu aux \(m-1\) questions et pas à la \(m\) ieme question posée ;
\(P(X = m) = \) \(0,10 \times {\left( {0,90} \right)^m}\)
2. Le nombre \({m_0}\) le plus favorable de questions supplémentaires qui peuvent être posées au candidat est le nombre correspondant à X ayant la valeur maximale de la probabilité \({m_0} = 1\)

Correction exercice VI

Les différentes valeurs que peuvent prendre les variables aléatoires X et Y sont :
• X = 1 ; 2 ; 3 ; … ; m ; …
• Y =1 ; 2 ; 3 ; … ; m ; …
D’où les probabilités
• Pour \(X =1\), on a \(P(X = 1) = 0,30\) c'est-à-dire que la première balle tirée par la première arme a atteint la cible.
• Pour \(X =2\) : \(P(X = 2) = \) \(0,7{\left( {0,30} \right)^2}\)
• Pour \(X =3\) : \(P(X = 3) = \) \({\left( {0,7} \right)^2}{\left( {0,30} \right)^3}\)
• Pour \(X = m\) \(P(X = m) = \) \({\left( {0,7} \right)^{m - 1}}{\left( {0,30} \right)^m}\)
• Pour \(Y =2\), on a \(P(Y = 2) = 0,30\)
• \(P(Y = 2) = {\left( {0,7} \right)^3}\) \(\left( {0,30} \right)\)
• \(P(Y = 3) = {\left( {0,7} \right)^4}\) \({\left( {0,30} \right)^2}\)
• \(P(Y = m) = \) \({\left( {0,7} \right)^{m + 1}}{\left( {0,30} \right)^{m - 1}}\)
On rappelle que les tirs avec la première et la seconde arme s’altèrent.
On en déduit les lois de répartition de X et Y.

Correction Exercice VII

A. 1.
Calculons l’espérance mathématique \(E(X)\)
\(E(X) = - 4\frac{2}{{10}}\) \( + 6\frac{3}{{10}} + 10\frac{5}{{10}} = 6\)
Calculons l’espérance mathématique \(E(Y)\)
\(E(X) = 0,21\frac{1}{{10}}\) \( + 0,54\frac{5}{{10}} + 0,61\frac{4}{{10}}\) \( = \frac{{53,5}}{{100}}\)
2. Calculons les espérances mathématiques \(E\left( {{X_1}} \right)\) et \(E\left( {{Y_1}} \right)\)
\(E(X) = E({X_1} + 2{Y_1})\) \( = E({X_1}) + \) \(2E({Y_1}) = 6\)
\(E(Y) = E(3{X_1} + 4{Y_1})\) \( = 3E({X_1}) + 4E({Y_1})\) \( = \frac{{53,5}}{{100}}\)
D’où le système d’équation
\(\left\{ \begin{array}{l} E({X_1}) + 2E({Y_1}) = 6\\ 3E({X_1}) + 4E({Y_1}) = \frac{{53,5}}{{100}} \end{array} \right.\)
Dont la résolution permet d’avoir \(E({X_1})\) et \(E({Y_1})\)
B. Nous avons : \(E(X) = 0,2\) et \(E({X^2}) = 0,4\),
Calculons les probabilités \({p_1}\), \({p_1}\) et \({p_1}\)
\(\sum\limits_i {{p_i}} = 1 \Leftrightarrow \) \({p_1} + {p_2} + {p_3}\) \( = 1\)
\(E(X) = - 1 \times {p_1} + \) \(0 \times {p_2} + 1 \times {p_3} = \) \( - {p_1} + {p_3} = 0,2\)
\(E({X^2}) = {\left( { - 1} \right)^2} \times {p_1}\) \( + {1^2} \times {p_3} = {p_1} + {p_3}\) \( = 0,4\)
Apres avoir résolu ce système de trois équation à trois inconnues, nous avons :
\(\left\{ \begin{array}{l} {p_1} = 0,1\\ {p_2} = 0,6\\ {p_3} = 0,3 \end{array} \right.\)

Correction exercice VIII

1. Calculons la dispersion de la variable Z tel que \(Z = 3X + 2Y\)
\(V(Z) = V(3X + 2Y)\) \( = V(3X) + V(2Y)\) \( = {3^2}V(X) + {2^2}V(Y)\)
Ceux-ci d’après la propriété \(V(aX) = {a^2}V(X)\)
D’où \(V(Z) = {3^2} \times 5 + \) \({2^2} \times 6 = 69\)
2. Calculons la dispersion de X
\(V(X) = E({X^2})\) \( - {\left( {E(X)} \right)^2}\)
\(E(X) = - 0,3\)
\(E({X^2}) = 15,3\)
\(V(X) = 15,3 - \) \(0,09 = 15,21\)
Calculons l’écart quadratique moyen de X.
\(\sigma (X) = \) \(\sqrt {V(X)} = 3,9\)