I Limite en l’infini des fonctions polynômes et rationnelles
Dans le cours nous avons montré que :
La limite en l’infini d’un polynôme est égale à la limite en l’infini de son monôme de plus haut degré
La limite en l’infini d’une fraction rationnelle est égale à la limite en l’infini du quotient des monômes de plus haut degré du numérateur et du dénominateur
Correction exercice I
Calcule des limites des polynômes
• \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) \( = \mathop {\lim }\limits_{x \to + \infty } \left( {5{x^3} - x + 1} \right)\) \( = \mathop {\lim }\limits_{x \to + \infty } 5{x^3} = + \infty \)
• \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \) \(\mathop {\lim }\limits_{x \to - \infty } \left( {5{x^3} - x + 1} \right)\) \( = \mathop {\lim }\limits_{x \to - \infty } 5{x^3} = - \infty \)
• \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \) \(\mathop {\lim }\limits_{x \to + \infty } \left( {1 - 2{x^2} + 3x} \right)\) \( = \mathop {\lim }\limits_{x \to + \infty } - 2{x^2}\) \( = - \infty \)
• \(\mathop {\lim }\limits_{x \to - \infty } g(x) = \) \(\mathop {\lim }\limits_{x \to - \infty } \left( {1 - 2{x^2} + 3x} \right)\) \( = \mathop {\lim }\limits_{x \to - \infty } - 2{x^2}\) \( = - \infty \)
2. Calculons les limites en \( - \infty \) et \( + \infty \) de la fonction rationnelle suivante :
• \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \) \(\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{7{x^5} - 4{x^3} + 1}}{{{x^2} - x + 6}}} \right)\) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{7{x^5}}}{{{x^2}}}\) \( = \mathop {\lim }\limits_{x \to - \infty } 7{x^3}\) \( = - \infty \)
• \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \) \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{7{x^5} - 4{x^3} + 1}}{{{x^2} - x + 6}}} \right)\) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{7{x^5}}}{{{x^2}}}\) \( = \mathop {\lim }\limits_{x \to + \infty } 7{x^3}\) \( = + \infty \)
• \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \) \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{ - 3x + 4{x^3} + {x^2} - 1}}{{{x^2} - 1 + x}}} \right)\) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{4{x^3}}}{{{x^2}}}\) \( = \mathop {\lim }\limits_{x \to + \infty } 4x\) \( = + \infty \)
• \(\mathop {\lim }\limits_{x \to - \infty } g(x) = \) \(\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - 3x + 4{x^3} + {x^2} - 1}}{{{x^2} - 1 + x}}} \right)\) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{4{x^3}}}{{{x^2}}}\) \( = \mathop {\lim }\limits_{x \to - \infty } 4x\) \( = - \infty \)
II Limite au bornes du domaine de définition des fonctions polynômes et rationnelles
Correction exercice II
1. Le domaine de définition des fonctions polynômes est \(Df = \) \( \mathbb{R}\) \( = \left] { - \infty ; + \infty } \right[\), le calcul des limites aux bornes de son domaine de définition se résumerait au calcul des limites en \({ - \infty }\) et \({ + \infty }\)
2. Calculons les limites de la fonction suivante aux bornes de son domaine de définition
\(f(x) = \frac{{x + 1}}{{x - 2}}\)
Expression du domaine de définition
\(Df = \) \( \mathbb{R}\) \( - \left\{ 2 \right\}\) \( = \left] { - \infty ;2} \right[ \cup \left] {2; + \infty } \right[\)
Tableau de signe du dénominateur 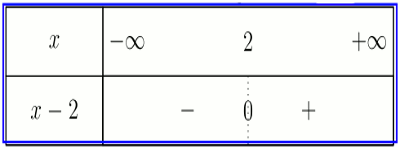
• \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \) \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \) \(\mathop {\lim }\limits_{x \to + \infty } \frac{x}{x} = 1\)
• \(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{x + 1}}{{x - 2}} = \) \( - \infty \) \(\left\{ \begin{array}{l}x + 1 \to 3\\x - 2 \to 0\\x - 2 \prec 0\end{array} \right.\)
• \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x + 1}}{{x - 2}}\) \( = + \infty \) \(\left\{ \begin{array}{l}x + 1 \to 3\\x - 2 \to 0\\x - 2 \succ 0\end{array} \right.\)
Calculons des limites aux bornes du domaine de définition
\(g(x) = \) \(\frac{{{x^2} - x + 1}}{{2{x^2} + 1}}\)
Expression du domaine de définition de \(g(x)\)
\(Dg = \left] { - \infty ; + \infty } \right[\)
Car \(2{x^2} + 1 \ne 0\) \( \Rightarrow {x^2} \ne - \) \(\frac{1}{2}\) toujours vraie
• \(\mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - x + 1}}{{2{x^2} + 1}}\) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - x + 1}}{{2{x^2} + 1}}\) \( = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}}}{{2{x^2}}}\) \( = \frac{1}{2}\)
• \(\mathop {\lim }\limits_{x \to - + \infty } \frac{{{x^2} - x + 1}}{{2{x^2} + 1}}\) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - x + 1}}{{2{x^2} + 1}}\) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}}}{{2{x^2}}}\) \( = \frac{1}{2}\)
III. Limite d’une fonction composée
Correction exercice III
1. Calculons \(\mathop {\lim }\limits_{x \to - \frac{3}{2}} \frac{{\sin (2x + 3)}}{{2x + 3}}\)
\(\frac{{\sin (2x + 3)}}{{2x + 3}}\) \( = g \circ f(x)\) avec \(f(x) = 2x + 3\) et \(g(x) = \frac{{\sin x}}{x}\)
\(\mathop {\lim }\limits_{x \to - \frac{3}{2}} \left( {2x + 3} \right)\) \( = 0\)
\(\mathop {\lim }\limits_{x \to 0} g(x) = \) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin \left( {2x + 3} \right)}}{{2x + 3}}\) \( = 1\)
2. Soient \(f(x) = \frac{{x + 1}}{{x - 1}}\), calculons \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) et en déduire \(\mathop {\lim }\limits_{x \to + \infty } f \circ f(x)\) et \(\mathop {\lim }\limits_{x \to - \infty } f \circ f(x)\)
\(Df = \) \( \mathbb{R}\) \(\backslash \left\{ {\frac{1}{2}} \right\}\)
Pour \({x \ne \frac{1}{2}}\), \(f(x) - \frac{1}{2}\) \( = \frac{3}{{2\left( {2x - 1} \right)}}\) \( \ne 0\), donc \(f \circ f(x)\) est definie sur \( \mathbb{R}\) \(\backslash \left\{ {\frac{1}{2}} \right\}\)
\(\mathop {\lim }\limits_{x \to + \infty } \left( {f(x) - \frac{1}{2}} \right)\) \( = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{2\left( {2x - 1} \right)}}\) \( \to 0 \Rightarrow \) \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) \( \to \frac{1}{2}\) avec \(f(x) \succ \frac{1}{2}\) pour \(x \succ \frac{1}{2}\)
Lorsque \(y\) tend vers \(\frac{1}{2}\) avec \(y \succ \frac{1}{2}\), \(y + 1\) tend vers 0 en restant positif, donc \(f(y) = \) \(\frac{{y + 1}}{{2y - 1}}\) tend vers \({ + \infty }\)
Ainsi \(\mathop {\lim }\limits_{x \to + \infty } f(f(x))\) \( = + \infty \)
De même \(\mathop {\lim }\limits_{x \to - \infty } f(f(x))\) \( = - \infty \)
Pour \(x \ne \frac{1}{2}\),
\(f(f(x)) = \) \(\frac{{\frac{{x + 1}}{{2x - 1}} + 1}}{{2\frac{{x + 1}}{{2x - 1}} - 1}}\) \( = x\), ce qui donne évidemment les résultats précédents
3. Calculons la limite de \(h(x) = x\sin \frac{1}{x}\) en \( + \infty \)
Soient \(f\) et \(g\) deux fonctions définies par : \(f(x) = \frac{1}{x}\) et \(g(x) = \frac{{\sin x}}{x}\),
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = 0\) et \(\mathop {\lim }\limits_{y \to 0} g(y) = 1\)
IV Théorème de comparaison
Exercice IV
1. Calculons les limites en \( - \infty \) et \( + \infty \) de la fonction \(f(x) = 2x + \) \(1 - 3\sin x\)
En effet : \(\forall x \in \) \( \mathbb{R}\), \( - 1 \le \sin x \le 1\) donc \(\forall x \in \) \( \mathbb{R}\), \(2x - 2 \le \) \(f(x) \le 2x + 4\)
\(\mathop {\lim }\limits_{x \to + \infty } \left( {2x - 2} \right)\) \( \to + \infty \) donc \(\mathop {\lim }\limits_{x \to + \infty } f(x) \to \) \( + \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } \left( {2x + 4} \right)\) \( \to - \infty \) donc \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) \( \to - \infty \)
2. En utilisant les propriétés de comparaison, calculons les limites en et des fonctions suivantes : en procèdent comme précédemment, vous trouverez :
a) \(f(x) = - 4x + 3\) \( - \cos x\) ;
\(\forall x \in \) \( \mathbb{R}\), \( - 4x + 2 \le f(x)\) \( \le - 4x + 4\) donc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \) et \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty \)
b) \(g(x) = \) \(\frac{{x\sin x}}{{{x^2} + 1}}\) ;
\(\forall x \in \) \( \mathbb{R}\), \(\left| {g(x)} \right| \le \) \(\frac{{\left| x \right|}}{{{x^2} + 1}}\) donc \(\mathop {\lim }\limits_{x \to + \infty } g(x) = 0\) et \(\mathop {\lim }\limits_{x \to - \infty } g(x) = 0\)
c) \(t(x) = {x^2}\) \( + 2\sin x\) ;
\(\forall x \in \) \( \mathbb{R}\), \({x^2} - 2 \le t(x)\) \( \le {x^2} + 2\) alors \(\mathop {\lim }\limits_{x \to + \infty } t(x) = + \infty \) et \(\mathop {\lim }\limits_{x \to - \infty } t(x) = + \infty \)
d) \(u(x) = \) \({x^3}(2 + \cos x)\).
\(\forall x \in \) \(\left[ {0; + \infty } \right[\), \(u(x) \ge {x^3}\) donc \(u(x) \ge {x^3}\) \(\mathop {\lim }\limits_{x \to + \infty } u(x) = + \infty \)
\(\forall x \in \) \(\left] { - \infty ;0} \right]\); \(u(x) \le {x^3}\) donc \(\mathop {\lim }\limits_{x \to - \infty } u(x) = - \infty \)
V. Théorème des gendarmes
Correction exercice V
1. Calculons la limite en 0 de la fonction \(g(x) = xE\left( {\frac{1}{x}} \right)\) où E désigne la fonction partie entière
\(\forall x \in \) \( \mathbb{R}\), \(E(x) \le x\) \( \le E(x) + 1\), donc \(\forall x \in \) \( \mathbb{R^*}\), \(\frac{1}{x} - 1 \le \) \(E\left( {\frac{1}{x}} \right) \le \frac{1}{x}\).
On en déduit que \(\forall x \in \left] {0; + \infty } \right[\), \(1 - x \le g(x) \le 1\) ; donc \(\mathop {\lim }\limits_{x \to {0^ + }} g(x) = 1\)
De meme, on a \(\forall x \in \left] { - \infty ;0} \right[\), \(1 \le g(x) \le 1 - x\) donc \(\mathop {\lim }\limits_{x \to {0^ - }} g(x) = 1\)
On a \(\mathop {\lim }\limits_{x \to {0^ - }} g(x) = \) \(\mathop {\lim }\limits_{x \to {0^ + }} g(x) = 1\) donc \(\mathop {\lim }\limits_{x \to 0} g(x) = 1\)
2. Calculons la limite \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \sin x}}{{x + 1}}\)
En effet : \( - 1 \le sinx\) \( \le 1 \Leftrightarrow 1 \le 2\) \( + sinx \le 3 \Leftrightarrow \) \(\frac{1}{{x + 1}} \le \frac{{2 + sinx}}{{x + 1}}\) \( \le \frac{3}{{x + 1}}\)
Apres encadrement de la fonction \(f(x)\), nous avons
\(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} \le \) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 + sinx}}{{x + 1}}\) \( \le \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 1}}\) soit \(0 \le \) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 + sinx}}{{x + 1}}\) \( \le 0\)
Ainsi
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2 + sinx}}{{x + 1}} = 0\)
VI. Forme indéterminée
Correction exercice VI
1. Calculons la limite en 0 de la fonction \(f(x) = \frac{{\sin 2x}}{{\sin 5x}}\)
\(f(x) = \frac{{\sin 2x}}{{\sin 5x}}\) \( = \frac{{\sin 2x}}{{2x}} \times \frac{{2x}}{{5x}} \times \) \(\frac{{5x}}{{\sin 5x}} = \frac{{\sin 2x}}{{2x}}\) \( \times \frac{{2}}{{5}} \times \frac{1}{{\frac{{\sin 5x}}{{5x}}}}\)
\(\mathop {\lim }\limits_{x \to 0} f(x) = \) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{2x}} \times \frac{2}{5} \times \) \(\frac{1}{{\mathop {\lim }\limits_{x \to 0} \frac{{\sin 5x}}{{5x}}}}\) \( = \frac{2}{5}\)
2. Calculons la limite en \(\frac{\pi }{4}\) de la fonction \(f(x) = \) \(\frac{{\sin x - \cos x}}{{x - \frac{\pi }{4}}}\)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin x - \cos x}}{{x - \frac{\pi }{4}}}\) \( = \frac{0}{0}\) forme indéterminée
Levons l’indétermination
\(\sin x - \cos x\) \( = \sin x - \) \(\sin \left( {\frac{\pi }{2} - x} \right) = \) \(2\sin \left( {x - \frac{\pi }{4}} \right)\) \(\cos \left( {\frac{\pi }{4}} \right) = \) \(\sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)\)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)}}{{x - \frac{\pi }{4}}}\) \( = \sqrt 2 \)
3. Calculons la limite en 1 de la fonction \(f(x) = \frac{{x - 1}}{{{x^2} - 1}}\)
\(\mathop {\lim }\limits_{x \to 1} f(x) = \) \(\mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{{x^2} - 1}}\) \( = \frac{0}{0}\) forme indéterminée
Levons l’indétermination
\(\frac{{x - 1}}{{{x^2} - 1}} = \) \(\frac{{x - 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\) \( = \frac{1}{{x + 1}}\)
\(\mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{{x^2} - 1}} = \) \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{x + 1}}\) \( = \frac{1}{2}\)
VII. Théorème de l’Hôpital
Exercice VII
1. Calculons la limite en 1 de la fonction : \(h(x) = \) \(\frac{{{{\left( {x - 1} \right)}^2}}}{{{x^2} – 3x + 2}}\) \( = \frac{{f(x)}}{{g(x)}}\)
Conditions
• \(f(1) = g(1) = 0\)
• \(g'(1) \ne 0\)
ainsi
• \(\mathop {\lim }\limits_{x \to 1} h(x) = \) \(\mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{{g(x)}} = \) \(\frac{{f'(1)}}{{g'(1)}}\)
Soit \(\mathop {\lim }\limits_{x \to 1} h(x) = \) \(\frac{{f'(1)}}{{g'(1)}} = \) \(\frac{{2\left( {1 - 1} \right)}}{{2 \times 1 - 3}} = \) \(\frac{0}{{ - 1}} = 0\)
2. Calculons la limite en 1 de la fonction \(h(x) = \) \( = \frac{{\frac{{{{\left( {x - 1} \right)}^2}}}{{{x^2} - 3x + 2}}}}{{{x^2} - 5x + 4}}\)
En procèdent comme précédemment vous trouverez :
\(\mathop {\lim }\limits_{x \to \infty } h(x) = \frac{1}{3}\)


