Exercice 1 : Chimie organique /6pts
1.1 Équation bilan de la réaction
\({C_n}{H_{2n}} + \) \({H_2}O\) \(\overbrace \to ^{{H_2}S{O_4}}\) \(\:{C_n}{H_{2n + 2}}O\)(0,5 pt)
La fonction de B : C’est un alcool (0,25 pt)
1.2 Formule brute de B
\(\% O = \frac{{1600}}{{14n + 18}}\) \( = 21,6\) \( \Rightarrow n = 4\)(0,25 pt)
B est dont de formule brute : \({C_4}{H_{10}}O\)
1.3 Les formules semi-développés possibles de B (0,25x4=1pt)
a) \({H_3}C - \) \(C{H_2} - \) \(C{H_2} - \) \(C{H_2}OH\)
b) \(\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2}OH}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}\)
c) \(\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2} - CH3}\\{}&|&{}\\{}&{OH}&{}\end{array}\)
d) \(\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&{C - }&{C{H_3}}\\{}&|&{}\\{}&{OH}&{}\end{array}\)
1.3 Formules semi-développées de A et B (0,25x2=0,5 pt)
A : \(\begin{array}{*{20}{c}}{{H_3}C - }&C&{ = C{H_2}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}\)
B : \(\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&C&{ - C{H_3}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}\)
2.1 Équation-bilan de la réaction
\(\begin{array}{*{20}{c}}{{H_3}C - }&{\bar N}&{C{H_3}}\\{}&|&{}\\{}&{C{H_3}}&{}\end{array}\) \( + {H_3}C - C{H_2}\) \( - C{H_2} - I\) \( \to \) \(\begin{array}{*{20}{c}}{}&{C{H_3}}&{}\\{}&|&{}\\{{H_3}C - }&{{N^ + }}&{ - C{H_3}}\\{}&|&{}\\{}&{{{(C{H_2})}_3} - C{H_3}}&{}\end{array}\) \( + {I^ - }\) (0,5pt)
2.2 Nom du produit formé : Iodure de butyltriméthylammonium. (0,5 pt)
2.3. Le caractère de l’amine mis en évidence est caractère nucléophile (0,5pt)
3.1 Formule générale des α-aminés (0,5 pt)
\(\begin{array}{*{20}{c}}{R - }&{CH}&{ - COOH}\\{}&|&{}\\{}&{N{H_2}}&{}\end{array}\)
3.2 Formule brute de l’acide α-aminé : en posant \(R = {C_n}{H_{2n + 1}}\), on a : \(M = 14n + 75\) \( = 131\)
\(n = 4\)(0,5 pt)
d’où la formule brute \({C_6}{H_{13}}{O_2}N\) (0,5 pt)
3.3 Formule semi-développée de l’acide α-aminé (0,5pt)
\(\begin{array}{*{20}{c}}{{H_3}C - }&{CH}&{ - C{H_2} - }&{CH}& - &{COOH}\\{}&|&{}&|&{}&{}\\{}&{C{H_3}}&{}&{N{H_2}}&{}&{}\end{array}\)
Acide –amino 4-méthylpentanoïque (0,5pt)
Exercice 2 : Acides-Bases /06pts
1. Un acide fiable est un acide qui se dissocie partiellement dans l’eau (0,5pt)
2.1. Calcule de \([{H_3}{O^ + }]\)
\(pH = \) \( - \log ([{H_3}{O^ + }])\) \( \Rightarrow \) \([{H_3}{O^ + }] = {10^{ - pH}}\)(0,25pt)
AN : \([{H_3}{O^ + }] = \) \({10^{ - 3,4}} \approx \) \(4 \times {10^{ - 4}}\) mol/L (0,25 pt)
2.2 Montrons que l’acide éthanoïque est acide faible (0,5 pt)
\([{H_3}{O^ + }] = 4 \times {10^{ - 4}}\) mol/L \({C_2} = {10^{ - 2}}\) mol/L
\([{H_3}{O^ + }] \prec {C_2}\) donc \(C{H_3}COOH\) est un acide faible
2.3 Équation bilan de l’acide éthanoïque avec de l’eau (0,75pt)
\(C{H_3}COOH\) \( + {H_2}O\) \( \mathbin{\lower.3ex\hbox{\(\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}\)}} \) \(C{H_3}CO{O^ - }\) \( + {H_3}{O^ + }\)
2.4 Calcule de la concentration des espèces en solution
Espèces en solution :
Ions : \({H_3}{O^ + }\) , \(C{H_3}CO{O^ - }\) , \(H{O^ - }\)
Molécules : \(C{H_3}COOH\), \({H_2}O\)
\(2{H_2}O\) \( \mathbin{\lower.3ex\hbox{\(\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}\)}} \) \({H_3}{O^ + }\) \( + H{O^ - }\)
\([{H_3}{O^ + }][H{O^ - }]\) \( = Ke\)
\([H{O^ - }] = 2,5 \times {10^{ - 11}}\) mol/L (0,25pt)
\([{H_3}{O^ + }] \approx \) \([C{H_3}CO{O^ - }]\) \( = 4 \times {10^{ - 4}}\) mol/L
\([C{H_3}COOH] + \) \([C{H_3}CO{O^ - }] = \) \({C_2}\)
\([C{H_3}COOH]\) \( = 9,6 \times {10^{ - 3}}\) mol/L (0,25pt)
- pKa de l’acide
\(pH = pKa\) \( + \log \frac{{[C{H_3}CO{O^ - }]}}{{[C{H_3}COOH]}}\)
\(pKa \approx 4,8\) (0,25pt)
3. Dosage acide/base
3.1 Calcule de Ca
\({n_a} = {n_b}\) \( \Leftrightarrow \) \({C_a}{V_a} = {C_b}{V_b}\) (0,25pt)
\({n_a} = {n_b}\) \( \Leftrightarrow \) \({C_a} = \frac{{{C_b}{V_b}}}{{{V_a}}}\)
\({C_a} = 0,2\) mol/L (0,25 pt)
3.2 Calcule de la masse molaire (1 pt)
\(C = \frac{n}{V}\) \( = \frac{m}{{MV}}\) \( \Rightarrow M = \) \(\frac{m}{{CV}} = 102\) mol/L
Formule brute de l’acide
\(M = \) \(14n + 32 = \) \(102 \Rightarrow \) \(n = 5\)
D’où la formule brute est : \({C_5}{H_{10}}{O_2}\)
Exercice 3 : Chimie générale /4points
1.1. Niveau d’’énergie
L’énergie d’ionisation est l’énergie minimale à fournir à un atome pris dans son état fondamental afin de lui arracher son électron.
1.2.1 Il y a absorption des photons parce que l’électron passe d’énergie inférieur (n=1) aa un niveau d’énergie supérieur (p˃1)
Posons \({E_0} = 13,6eV\)
\(\Delta E = Ep\) \( - En \Rightarrow \) \(\upsilon = \frac{{13,6}}{h}\) \(\left( {1 - \frac{1}{{{p^2}}}} \right)\) (0,5pt)
1.2.3. Calcule de \(\upsilon \) pour \(p = 3\)
\(\upsilon = 2,92 \times {10^{15}}\) Hz
2. Cinétique chimique
2.1 Montrons que les ions \({I^ - }\) sont en excès
\(\frac{{{n_{{H_2}{O_2}}}}}{1} = \frac{{{C_1}{V_1}}}{1}\) \( \Rightarrow \) \({n_{{H_2}{O_2}}} = \) \(4,5 \times {10^{ - 3}}\) mol
\(\frac{{{n_{{I^ - }}}}}{2} = \) \(\frac{{{C_2}{V_2}}}{1} = {10^{ - 2}}\) mol
\(\frac{{{n_{{I^ - }}}}}{2} \succ \frac{{{n_{{H_2}{O_2}}}}}{1}\)
Donc les ions \({I^ - }\) sont en excès
2.2. On ajoute la glace pour bloquer la réaction d’oxydation des ions iodure par l’eau oxygénée dans le bécher (0,5 pt)
2.3. L’expression de la concentration de \({I_2}\)
Équation de réaction
\({I_2} + \) \(2{S_2}O_3^{2 - }\) \( \to \) \(2{I^ - } + \) \({S_4}O_6^{2 - }\)
A l’équivalence,
\(\frac{{{n_{{I_2}}}}}{1} = \frac{{{n_{{S_2}O_3^{2 - }}}}}{2}\) \( \Rightarrow [{I_2}]V\) \( = \frac{{[{S_2}O_3^{2 - }]}}{2}{V_{{S_2}O_3^{2 - }}}\)
\({[{S_2}O_3^{2 - }] = C'}\) et \({V_{{S_2}O_3^{2 - }}} = V'\) On a dont
\([{I_2}] = \frac{{C'}}{{2V}}V'\) (0,25pt)
2.4. Calcule de la concentration \({[{I_2}]_t}\) à la fin de la réaction
\({H_2}{O_2} + \) \(2{I^ - } + \) \(2{H_3}{O^ + }\) \( \to \) \({I_2} + \) \(4{H_2}O\)
L’eau oxygénée étant le réactif en défaut sera totalement consommé à la fin de la réaction. Dans le bêcher, on a :
\({[{I_2}]_t} = \frac{{{{({n_{{I_2}}})}_{formée}}}}{{{V_1} + {V_2}}}\)
Or \({({n_{{I_2}}})_{formée}}\) \( = {({n_{{H_2}{O_2}}})_{disparu}}\) \( = {C_1}{V_1}\)
\({[{I_2}]_t} = \) \( = \frac{{{C_1}{V_2}}}{{{V_1} + {V_2}}}\) \( = \frac{{{C_1}}}{2}\) car \({{V_1} = {V_2}}\)
\({[{I_2}]_t} = 2,25 \times {10^{ - 2}}\) mol/L à la fin de la réaction
Exercice 4 : Caractère expérimental /4 points
1.1 Calcule du volume V0 de la solution à prélever, En appliquant la loi de la dilution, on a :
\({C_0}{V_0} = CV\) \( \Rightarrow {V_0} = \frac{{CV}}{{{C_0}}}\) (0,5pt)
\({V_0} = 10\) mL
1.2. Deux éléments nécessaires pour la préparation
La fiole jaugée de 250 Ml et la pipette jaugée de 10 Ml
1.2 Mode opératoire
A l’aide d’une pipette jaugée de 10 mL, prélever 10 mL de la solution S0 et l’introduire dans une fiole jaugée de 250 mL contenant au préalable une quantité d’eau distillée. Complétons le volume dans la fiole jaugée avec l’eau distillée jusqu’au trait de jauge et homogénéiser.
2. Vérification de la concentration
2.1. Construction du diagramme \(pH = f(Vb)\)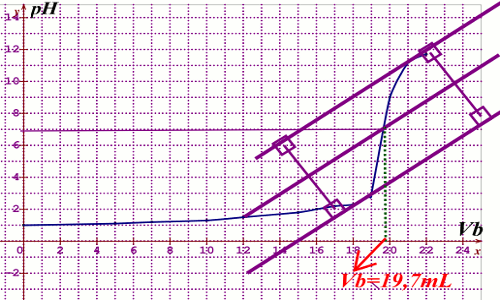
2.2. En utilisant la méthode des tangentes, on trouve à l’équivalence un volume \(Vb = 19,7\) d’hydroxyde de sodium. (voir millimétrée)
2.3. Calcule de \(Ca\)
A l’équivalence
\(Ca = \frac{{VbCb}}{{Ca}} = 0,098\) mol/L
2.4. \(Ca \approx C = 0,1\) mol/L
Le dosage a permis de vérifier que la solution S d’acide chlorhydrique a été bien préparée
