Baccalauréat
Physique
D
2011
Enoncés
Bonjour ! Groupe telegram de camerecole, soumettrez-y toutes vos préoccupations. forum telegram
Exercice 1: Mouvement dans les champs et leurs applications
Les questions 1) et 2) sont indépendantes
1) Etude du champ électrique créé par des charges ponctuelles
Deux charges électrostatiques ponctuelles q1 et q2 sont respectivement aux points A et B, distant de 10 cm. On donne q1=+10-8 C; q2=-10-8 C; k=9 109 U.S.I.
1.1. Représenter sur le schéma la force électrique \(\overrightarrow F \) à laquelle est soumise la charge q2 , puis calculer son intensité.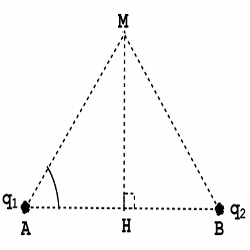
1.2. Quel est l’ensemble des positions qu’occuperait q2 dans le plan de la figure, pour que \(\overrightarrow F \) ait la même intensité que celle calculée ci-dessus?
1.3 Soit M, un point de la médiatrice du segment [AB], tel que l’angle \((\overrightarrow {AB} ;\overrightarrow {AM} ) = \theta = {60^0}\) (voir figure).
1.3.1. Représenter les champs \({\overrightarrow E _1}\) et \({\overrightarrow E _2}\) respectivement créés en M par q1 et q2 puis construire leur somme
1.3.2. Sachant que E1 = E2 = 9 103 N.C-1 , calculer la norme de \(\overrightarrow E \)
2) Shoot au basket-ball
Lors d’un shoot au basket-ball, le centre d’inertie G du ballon part d’un point O à la date t = 0, avec une vitesse initiale \(\overrightarrow {{v_0}} \) située dans le plan vertical contenant O et le centre P de l’anneau du panier. Le vecteur vitesse \(\overrightarrow {{v_0}} \) est incliné d’un angle α = 60° par rapport à l’horizontale. On considèrera que le joueur à marqué le panier si le centre d’inertie G du ballon passe par P. on étudie le mouvement de G dans le repère terrestre \((o,\overrightarrow i ,\overrightarrow j )\) dont l’origine O coïncide avec la position de G au départ. On négligera l’action de l’air. On prendra g = 10 m.s-1
2.1. En appliquant au ballon le théorème du centre d’inertie, montrer que l’accélération de son centre d’inertie G est égale à l’accélération de la pesanteur.
2.2. Etablir dans le repère \((o,\overrightarrow i ,\overrightarrow j )\) les équations paramétrique du mouvement de G.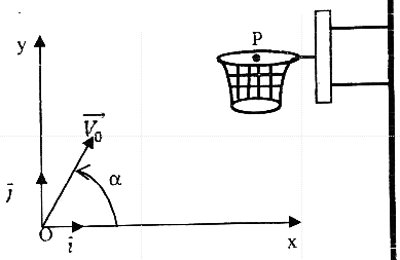
2.3. En déduire l’équation cartésienne de la trajectoire de G.
2.4. Vérifier que si v0 = 7,35 m/s, le joueur marquera le panier. On donne les coordonnées de P: Xp = 4 m; yp = 1 m.
Exercice 2: Les systèmes oscillants
Les questions 1) et 2) sont indépendantes.
1) Mesure de la fréquence d’une lame vibrante
On se propose de mesurer la fréquence f d’une lame vibrante, en utilisant un procédé stroboscopique.
Dans l’obscurité, on éclaire la lame à l’aide d’un stroboscope dont on fait croitre progressivement la fréquence fe des éclaires, à partie de sa plus petite valeur 20 Hz. La lame parait immobile (hors de sa position d’équilibre) pour certaines valeurs de fe , dont la plus grande est 100 Hz.
1.1. Donner une interprétation physique de l’immobilité apparente de la lame.
1.2. Ecrire la relation entre fe et f, puis calculer la valeur numérique de f.
1.3. Donner deux autres valeurs de fe pour lesquelles la lame parait immobile.
2) Etude d’un pendule simple
Un pendule simple est constitué par un fil inextensible de masse négligeable et de longueur ℓ = 0,9 m auquel est suspendu une masse ponctuelle. L’autre extrémité du fil est fixé en un point O. le pendule est écarté de sa position d’équilibre stable d’un angle θm puis abandonné sans vitesse. On néglige les frottements.
2.1. Etablir l’équation différentielle du mouvement du pendule pour θm quelconque compris entre 0 et 90°.
2.2. Dans le cas des oscillations de faible amplitude,
2.1.1. Donner une expression de la période propre T0 du pendule, puis calculer sa valeur numérique en prenant g = 9,8 m.s-2 ;
2.1.2. L’équation horaire du mouvement du pendule est de la forme . \(\theta (t) = {\theta _m}\cos (\omega t + \varphi )\) On a choisit pour instant initial l’instant où il passe pour la première fois par sa position d’équilibre, en allant dans le sens des élongations négatives. Déterminer la phase φ du mouvement à l’origine des dates.
Exercice 3: Phénomène vibratoire et corpusculaire
Les questions 1) et 2) sont indépendantes.
1) Propagation d’une vibration le long d’une corde élastique
Une corde élastique est reliée par son extrémité O à une lame d’un vibreur. La corde passe par la gorge d’une poulie et est étendue par une masse m suspendue à son autre extrémité (voir figure 3).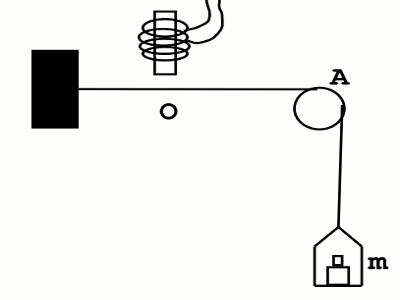
Lorsque le vibreur est mis en marche, une onde transversale de fréquence f = 100 Hz, se propage le long de la corde, avec célérité v = 20 m/s (on néglige l’amortissement de l’onde et la réflexion en A).
Lorsque le vibreur est mis en marche, une onde transversale de fréquence f = 100 Hz, se propage le long de la corde, avec célérité v = 20 m/s (on néglige l’amortissement de l’onde et la réflexion en A).1.1. Quand dit-on qu’une onde est transversale?
1.2. Calculer la longueur d’onde λ de cette onde.
1.3. Soit M un point de la corde, situé à x = 30 cm de O:
1.3.1. Comparer les mouvements vibratoires des points O et M;
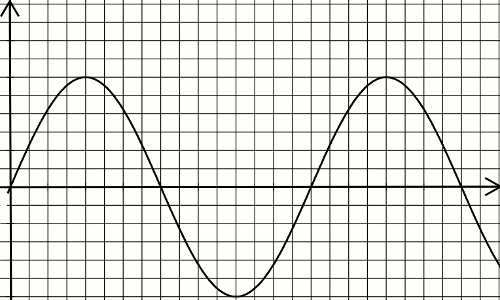
1.3.2. La ci-dessous représente les variations de l’élongation du point O, en fonction du temps.
Représenter sur le même graphique, les variations en fonction du temps, l’élongation du point M.
2) Radioactivité
« Lorsqu’un compteur Geiger-Muller est placé à coté d’une roche, on entend un crépitement dû à la radioactivité ».
2.1. Qu’est-ce que la radioactivité?
2.2. Le césium 137 est radioactif β-
2.2.1. Ecrire l’équation de désintégration d’un noyau de césium 137 extrait du tableau périodique:
2.2.2. La demi-vie du césium 137 est de 30 ans. Quelle est en années, la durée nécessaire pour que 90% des noyaux de césium contenus dans un échantillon se désintègrent?
|
Symbole des éléments |
I | Xe | Ce | Ba | La |
|---|---|---|---|---|---|
|
Numéro atomiques Z |
53 | 54 | 55 | 56 | 57 |
Exercice 4 : Expérience de physique
On dispose d’un pendule simple de longueur ℓ ajustable. On se propose d’étudier expérimentalement l’isochronisme des petites oscillations de ce pendule, puis les variations de sa période propre T0 en fonction de sa longueur ℓ.
1. Citer en dehors du pendule simple, trois autres éléments ou instruments faisant partie du matériel nécessaire à la réalisation des deux expériences.
2. Isochronisme des petites oscillations
On donne à ℓ la valeur ℓ0 = 1,00 m, puis on donne à l’amplitude θm des oscillations, des valeurs comprises entre 00 et 160 en mesurant à chaque fois la période propre T des oscillations.
2.1. Pour une valeur de θm , on obtient la période T correspondante en mesurant la durée Δt de 10 oscillations puis en divisant Δt par 10. expliquer pourquoi ce procédé permet de réduire l’erreur sur la mesure de T.
2.2. Le tableau de mesure est le suivant:
| \({\theta _m}{(^0})\) | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| T(s) | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | 2,01 | 2,01 |
Calculer la valeur numérique de la période propre des petits oscillations de ce pendule.
On prendra g = 9,81 N.Kg-1
2.2.2. Quelle conclusion relative à la période des oscillations peut-on tirer des valeurs de T obtenues ci-dessus?
3. Variations de la période propre T0 des petites oscillations en fonction de la longueur ℓ du pendules.
3.1. Décrire en quelques mots le mode opératoire.
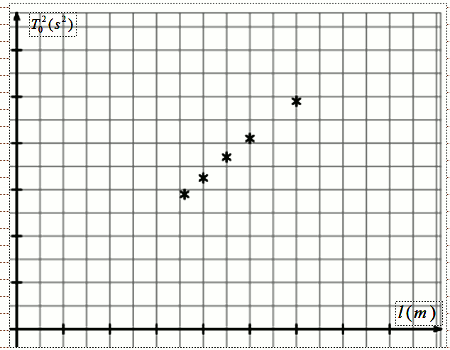
3.2. Les mesures réalisées permettent obtenir les points expérimentaux placés sur la figure 5 ci-dessous.
Échelle : 1cm pour 0,2 m; 1 cm pour 1 s2
3.2.1 Tracer la courbe \(T_o^2 = f(l)\)
Quelle conclusion peut-on en tirer?
3.2.2. En déduire une valeur expérimentale de l’intensité g de l’accélération de la pesanteur.
