Partie A : Évaluation des ressources : 15 points

Exercice 1 : 3,25 points

1. Justifions que \({M_{n + 1}}\) est l’image de \({M_{n}}\) par une transformation \(S\) 0,5 pt
Soit \(S\), une transformation d’écriture complexe \(z' = \frac{{1 - i}}{2}z\) , alors S est une similitude directe de centre O, d’angle \(\arg \left( {\frac{{1 - i}}{2}} \right) = - \frac{\pi }{4}\) et de rapport \({\left| {\frac{{1 - i}}{2}} \right| = \frac{{\sqrt 2 }}{2}}\)
On a bien \({M_{n + 1}} = S({M_n})\)
2. Déterminons l’image de la droite \((D)\) d’équation \(y=x\) par \(S\) 0,5 pt
En effet la droite \((D)\) passe par O, centre de S et \(Mes(\overrightarrow i ;\overrightarrow {OA} ) = \frac{\pi }{4}\) où \(A\) est un point quelconque de \((D)\).
L’image du point \(A\) est sur l’axe des abscisse, dont l(image de (D) est l’axe des abscisses, soit la droite d’équation \(y=0\)
3.a) Donnons la nature de la suite \(\left( {{v_n}} \right)\) et déduisons l’expression de \(\left| {{z_n}} \right|\) en fonction de \(n\) 0,5 pt
On a \({v_{n + 1}} = \left| {{z_n} - 1} \right| = \) \(\left| {\frac{{1 - i}}{2}{z_n}} \right| = \frac{{\sqrt 2 }}{2}{v_n}\)
Ainsi, \(\left( {{v_n}} \right)\) est une suite géométrique de raison \(\frac{{\sqrt 2 }}{2}\) et de premier terme \({v_o} = \left| { - 2} \right| = 2\). Donc \({v_n} = \left| {{z_n}} \right| = 2{\left( {\frac{{\sqrt 2 }}{2}} \right)^n}\).
3.b) Donnons la nature de la suite \(\left( {{u_n}} \right)\) et en déduisons en l’expression de \(\arg \left( {{z_n}} \right)\) en fonction de \(n\).
On a \({u_{n + 1}} = \arg \left( {{z_{n + 1}}} \right)\) \( = \arg \left( {\frac{{1 - i}}{2}{z_n}} \right) = \) \(\arg \left( {\frac{{1 - i}}{2}} \right) + \arg \left( {{z_n}} \right) = \) \( - \frac{\pi }{4} + \arg \left( {{z_n}} \right)\).
Ainsi, \(\left( {{v_n}} \right)\) est une suite arithmétique de raison \( - \frac{\pi }{4}\) et de premier terme \({u_o} = \arg ( - 2) = \pi \) . Donc \({u_n} = \arg \left( {{z_n}} \right) = \pi \) \( - \pi \frac{n}{4} = \pi \left( {1 - \frac{n}{4}} \right|\)
3.c) Déterminer les valeurs de \(n\) pour lesquelles \({M_n}\) appartient à la demi- droite \([Ox)\). \({M_n} \in [Ox)\) équivaut à \(\arg \left( {{z_n}} \right) = 0 + 2k\pi \) avec \(k \in Z\), \(\pi \left( {1 - \frac{n}{4}} \right) = 2k\pi \), ainsi, \(n = 4 - 8k\) 0,25pt
4.a) Calculons \(\frac{{{z_n} - {z_{n + 1}}}}{{{z_{n + 1}}}}\) et en déduisons en la nature exacte du triangle \(O{M_n}{M_{n + 1}}\) .
On a \(\frac{{{z_n} - {z_{n + 1}}}}{{{z_{n + 1}}}} = \) \(\frac{{{z_n} - \left( {\frac{{1 - i}}{2}} \right){z_n}}}{{\left( {\frac{{1 - i}}{2}} \right){z_n}}}\) \( = \frac{{1 + i}}{{1 - i}} = i\). Ainsi, le triangle est rectangle isocèle de sommet principal \({M_{n + 1}}\).
4.b) Calculons la limite de \((Ln)\) 0,5 pt
\(Ln = {M_0}{M_1} + \) \({M_1}{M_2} + ... + {M_{n - 1}}{M_n}\) \( = \left| {{z_1} - {z_0}} \right| + \left| {{z_2} - {z_1}} \right| + \) \(... + \left| {{z_n} - {z_{n - 1}}} \right|\)
\(\left| {\frac{{{z_n} - {z_{n + 1}}}}{{{z_{n + 1}}}}} \right| = \left| i \right| = 1\) soit
\(\left| {\frac{{{z_n} - {z_{n + 1}}}}{{{z_{n + 1}}}}} \right| = \left| i \right|\) \( = 1 \Rightarrow \left| {{z_n} - {z_{n + 1}}} \right|\) \( = \left| {{z_{n + 1}}} \right|\)
\(Ln = \sqrt 2 \left( {\frac{{1 - {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^{n + 1}}}}{{1 - \frac{{\sqrt 2 }}{2}}}} \right)\)
\(\mathop {\lim }\limits_{x \to + \infty } Ln = \frac{{\sqrt 2 }}{{1 - \frac{{\sqrt 2 }}{2}}}\) \( = \frac{{2\sqrt 2 }}{{2 - \sqrt 2 }}\)

EXERCICE 2

1. Étudions les variations de \(f\) puis construisons son tableau des variations 0,5 pt
On a \(f'(x) = - 2x - \) \(\frac{1}{{1 - x}} \prec 0\) donc \(f\) est strictement décroissante sur \(\left[ {0,1} \right[\)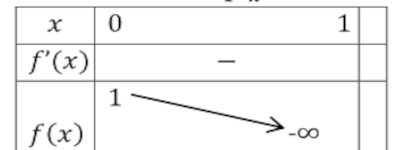
2. Construisons la courbe de \(f\)
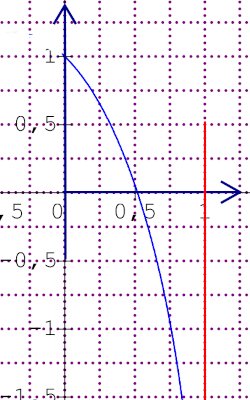3. Montrons que l’équation \(f(x)=0\) admet une solution unique \(\alpha \) et que \(\alpha \in \left[ {\frac{1}{2},1 - \frac{1}{e}} \right]\)
En effet, \(f\) est continue et strictement décroissante sur \(\left[ {0,1} \right[\) et réalise ainsi une bijection de \(\left[ {0,1} \right[\) vers \(\left] { - \infty ,1} \right]\) qui contient 0 d’où l’existence et l’unicité de\(\alpha \).
De plus \(f(\frac{1}{2}) = \frac{3}{4} - \ln 2 \succ 0\) et \(f(1 - \frac{1}{e}) = \) \(\frac{{2e - 1 - {e^2}}}{{{e^2}}} = \) \( - \left( {\frac{{e - 1}}{e}} \right) \prec 0\). D’où le résultat d’après le théorème des valeurs intermédiaires. 0,5 pt
4. Calculons \(I(t) = \int\limits_\alpha ^t {f(x)dx} \) 0,75 pt
On a \(\int\limits_\alpha ^t {f(x)dx} = \) \(\int\limits_\alpha ^t {(1 - {x^2})dx} + \) \(\int\limits_\alpha ^t {\ln (1 - x)dx} \)
En posant \(u'(x) = 1\), \(u(x) = x - 1\) et \(v(x) = \ln (1 - x)\) sur la deuxième intégrale, on a :
\(I(t) = [x - \frac{1}{3}{x^3} + \) \((x - 1)\ln (1 - x) - x]_\alpha ^t = \) \(t - \frac{1}{3}{t^3} + (t - 1)\ln (1 - t)\) \( - t - \alpha + \frac{1}{3}{\alpha ^3} - (\alpha - 1)\) \(\ln (1 - \alpha ) + \alpha \)
Or \(\ln (1 - \alpha ) = {\alpha ^2} - 1\) et \(\lim (t - 1)\ln (1 - t)\) lorsque \(t\) tend vers 1 est égale a 0, alors \(\mathop {\lim }\limits_{t \to 1} I(t) = - \frac{2}{3}{\alpha ^3}\) \( + {\alpha ^2} + \alpha - \frac{4}{3}\) d’où le résultat avec \(P(X) = - \frac{2}{3}{X^3} + {X^2}\) \( + X - \frac{4}{3}\).
5.a Etudions les variations de \(g\) et \(f\) et dresser leurs tableaux de variations.
On a \(h(x) = 2x + \frac{1}{{1 - x}}\) et \(g(x) = 2 + \frac{1}{{{{(1 - x)}^2}}}\), \(h'(x) = g(x) \succ 0\) et \(g'(x) = \frac{2}{{{{(1 - x)}^2}}} \succ 0\) Ainsi les fonctions \(h\) et \(g\) sont strictement croissante sur \(\left[ {0,1} \right[\).
5.b En déduisons en que : pour tout \(x\), \(\left[ {\frac{1}{2},1 - \frac{1}{e}} \right]\), \(\frac{{\left| {f''(x)} \right|}}{{\left| {f'(y)} \right|}} \le \frac{{{e^2} + 2}}{3}\)
En effet d’après les tableaux de variations, on a \({f'(y) \ge 3}\) , soit \(\frac{1}{{f'(y) \ge 3}} \le \frac{1}{3}\), comme \(f''(x) \le {e^2} + 2\) et \(f''(x) \ge 0\) ,le résultat en découle. 0,25pt
5.c Étudions la position relative de \((Cf)\) et de la tangente T0 au point d’abscisse 0.
On a \(f''(x) = - 2 - \) \(\frac{1}{{{{\left( {1 - x} \right)}^2}}} \prec 0\) sur \(\left[ {0,1} \right[\), ainsi, \(f\) est une fonction concave et sa courbe est en dessous de toutes ses tangentes, en particulier la tangente T0 0,5 pt

EXERCICE 3

1.a Démontrons par contraposée que si \({\alpha ^2}\) est pair, alors \(\alpha \) est pair.
Il suffit de démontrer que si \(\alpha \) n’est pas pair, alors \({\alpha ^2}\) n’est pas pair, soit si \(\alpha \) est impair, alors \({\alpha ^2}\) est impair
En effet a pair signifie que \(\alpha = 2k + 1\), \(k \in N\), alors \({\alpha ^2} = {\left( {2k + 1} \right)^2} = \) \(2(2{k^2} + 2k) + 1\) \( = 2k' + 1\). Donc \({\alpha ^2}\) est impair. D’où le résultat.
1.b) Déduisons-en que \(\sqrt 2 \)est irrationnel.
Supposons par l’absurde que \(\sqrt 2 \) est rationnel, c’est-à-dire qu’li existe deux entiers naturels non nuls \(m\) et \(n\) tels que \(\sqrt 2 = \frac{m}{n}\) avec \(\frac{m}{n}\)irréductible. \(\sqrt 2 = \frac{m}{n}\) entraine \({m^2} = 2{n^2}\) donc \({m^2}\) est pair et d’après 1) \(m \) est pair, soit \({m = 2k}\) et l’égalité \({m^2} = 2{n^2}\) signifie que \(4{k^2} = 2{n^2}\) , soit \(2{k^2} = {n^2}\) ; par suite\({n^2}\) et \(n\) sont pairs. Ainsi, \(n\) et \(m\) sont pairs, ce qui contredit le fait que\(\frac{m}{n}\) est irréductible.
1.c Montrons que si \(\alpha \) est premier, alors \(\sqrt \alpha \) est irrationnel
Supposons par l’absurde que \(\sqrt \alpha \) est rationnel, c’est-à-dire qu’il existe deux entiers naturels non nuls \(m\) et \(n\) tels que \(\sqrt \alpha = \frac{m}{n}\) avec \(\frac{m}{n}\)irréductible. \(\sqrt \alpha = \frac{m}{n}\) entraine \({m^2} = \alpha {n^2}\) donc \(\alpha \) divise \({m^2}\) et d’après le théorème de Gauss, \(\alpha \) divise \({m^2}\) car \({m^2}\) est premier. Ainsi, \(m = \alpha k\) et l’égalité \({m^2} = 2{n^2}\) signifie que \({\alpha ^2}{k^2} = \alpha {n^2}\), soit \(\alpha {k^2} = {n^2}\); par suite \({n^2}\), puis \(n\) sont divisibles par \(\alpha \). Ainsi, \(n\) et \(m\) sont divisibles par \(\alpha \), ce qui contredit le fait que \(\frac{m}{n}\). 0,5 pt
2.a Démontrons par récurrence que pour tous réels \(a\) et \( b\) et pour tout entier naturel \(n\) non nul, on a \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \)
• Pour \(n=1\), on a d’une part, \(a+b = a+b\) ;
• Soit \(n \succ 1\), supposons que \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \) et montrons que \({\left( {a + b} \right)^{n + 1}} = \sum\limits_{k = 0}^{n + 1} {C_{n + 1}^k{a^{n + 1 - k}}{b^k}} \)
En effet \({\left( {a + b} \right)^{n + 1}} = {\left( {a + b} \right)^n}\left( {a + b} \right)\) \( = \left( {a + b} \right)\sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \)
Partant de \(C_n^0 = C_{n + 1}^0\), \(C_n^n = C_{n + 1}^{n + 1}\) et \(C_n^i + C_n^{i + 1} = C_{n + 1}^{i + 1}\), on conclut que \(n \ge 1\), \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \).
2.b En déduisons en une écriture simple des nombres \(A = C_n^0 + C_n^1 + C_n^2\) \( + ... + C_n^n\) et \(A = C_n^0 - C_n^1 + C_n^2\) \( + ... + {( - 1)^n}C_n^n\)
• \({(1 + 1)^n} = \) \(\sum\limits_{k = 0}^n {C_n^k} {1^{n - k}}{1^k} = {2^n}\) ainsi \(A = {2^n}\)
• \({(1 - 1)^n} = \) \(\sum\limits_{k = 0}^n {C_n^k} {1^{n - k}}{\left( { - 1} \right)^k} = 0\), ainsi \(B = 0\)
3.a Déterminons le plus petit entier naturel \(n\) , pour que la probabilité \({p_n}\) d’obtenir au moins une fois un numéro strictement inférieur à 5 soit supérieur à 0,96 0,75 pt
Les \(n\) répétitions suivent un schéma de Bernoulli dont la probabilité d’obtenir un succès est \(\frac{2}{3}\), Ainsi, \({p_n} = 1 - {\left( {\frac{1}{3}} \right)^n}\) \( \succ 0,96 \Rightarrow {\left( {\frac{1}{3}} \right)^n}\) \( \prec 0,04\).
Soit \(n \succ \frac{{\ln \left( {0,04} \right)}}{{\ln \left( {\frac{1}{3}} \right)}} = 3\)

EXERCICE 4

1.a Démontrons que les droites \((D)\) et \((L)\) sont perpendiculaires en un point que l’on précisera.
En effet, en posant \(x=t\) alors une représentation paramétrique de \((D)\) est : \(\left\{ \begin{array}{l} x = 0 + t\\ y = - 3 + t\\ z = - 1 – t \end{array} \right.\)
Ainsi, les vecteurs \(\overrightarrow u (1;1 - 1)\) et \(\overrightarrow v (- 1;2 1)\) sont les vecteurs directeurs respectifs de \((D)\) et \((L)\). On a \(\overrightarrow u .\overrightarrow v = 0\). Donc \((D)\) et \((L)\) sont orthogonales.
Soit \(M(X,Y,Z)\) appartenant à \((D)\) et \((L)\). alors, \(\left\{ \begin{array}{l} t + 2t = - 3\\ - t - t - 1 = - 1 \end{array} \right.\) soit \(t=-1\) et par suite, le point \(I(1; - 2; - 2) \in \) \(\left( D \right) \cap \left( L \right)\) et \((D)\) et \((L)\) sont perpendiculaires. 0,75pt
1.b En déduisons en la nature et l’élément caractéristique de \({S_{(D)}} \circ {S_{(L)}}\).
\({S_{(D)}} \circ {S_{(L)}}\) est un demi d’axe \((D’)\) où \((D’)\) est la droite passant par \(I\) et orthogonale à la fois aux droites\((D)\) et \((L)\).
Ainsi \((D’)\) est la droite passant par \(I\) et de vecteur directeur \(\overrightarrow {u'} = \overrightarrow u \wedge \overrightarrow v \), soit \(\overrightarrow {u'} \left( {3;0;3} \right)\)
2. Déterminons l’expression analytique de \({S_{(P)}}\)
Soit \(M\left( {x;y;z} \right)\) et \(M\left( {x’;y’;z’} \right)\), son image par \( {S_{(P)}}\) , alors \(\overrightarrow {MM'} \) est colinéaire au vecteur normal \(\overrightarrow n \left( { - 1;2;1} \right)\) de \((P)\) et le milieu \(I(\frac{{x + x'}}{2};\frac{{y + y'}}{2}\) \(;\frac{{z + z'}}{2})\) appartient à \((P)\).
On a donc successivement, \(\left\{ \begin{array}{l} x' - x = - t\\ y' - y = 2t\\ z' - z = t \end{array} \right.;\) \( - \frac{{x + x'}}{2} + 2\frac{{y + y'}}{2}\) \( + \frac{{z + z'}}{2}\) \(=0\)
\( - \frac{{x + x'}}{2} + 2\frac{{y + y'}}{2}\) \( + \frac{{z + z'}}{2} = 0\), \(t = - \frac{1}{2}(x + \) \(2y + z)\) par suite \(\left\{ \begin{array}{l} x' = \frac{1}{2}\left( {3x + 2y + z} \right)\\ y' = - x - y - z\\ z' = \frac{1}{2}\left( { - x - y + z} \right) \end{array} \right.\)
3.a Déterminons la position relative de \((P)\) et de \((L)\)
Un vecteur normal \(\overrightarrow n \left( { - 1;2;1} \right)\) de \((P)\) est un vecteur directeur de \((L)\) , donc \((P)\) et \((L)\) sont perpendiculaires. 0,25pt
3.b En déduisons en la nature et l’élément caractéristique de \({S_{(P)}} \circ {S_{(L)}}\).
\({S_{(P)}} \circ {S_{(L)}}\) est la symétrie de centre \(B\) , point d’intersection de \((P)\) et \((L)\) Déterminons les coordonnées du point \(B\). On a : \(t + 4t + t\) \( - 1 = 0\) soit \(t = \frac{1}{6}\). Ainsi, \(B\left( { - \frac{1}{6};\frac{1}{3}; - \frac{5}{6}} \right)\)
4. Déterminons la nature et les éléments caractéristiques de \(\left( \Gamma \right)\)
\({y^2} + 4{z^2} - 2y - \) \(24z + 33 = 0\) équivaut à \({\left( {y - 1} \right)^2} + \) \(4{\left( {z - 3} \right)^2} - 4 = 0\)
Soit, \(\frac{{{{\left( {y - 1} \right)}^2}}}{4} + \frac{{{{\left( {z - 3} \right)}^2}}}{1} = 1\) Ainsi, \(\left( \Gamma \right)\) est une ellipse de centre \(C\left( {0;1;3} \right)\) , de grand axe (Oy) et d’excentricité \(e = \frac{{\sqrt 3 }}{2}\)
5.a Ecrire la matrice de l’endomorphisme \(f\) dans la base \((\overrightarrow i ;\overrightarrow j ;\overrightarrow k )\).
\(M = \left( {\begin{array}{*{20}{c}} 1&1&0\\ 1&1&{ - 2}\\ 1&1&1 \end{array}} \right)\)
Remarque : L’endomorphisme \(f\) qui vérifie les égalités ci-dessus n’est pas unique car \((\overrightarrow i + \overrightarrow j ;\overrightarrow j + \overrightarrow k ;\overrightarrow i - \overrightarrow k )\) n’est pas une base de l’espace.
5.b Déterminons le noyau \(kerf\) de l’endomorphisme \(f\)
Soit \(\overrightarrow u \left( {x;y;z} \right)\) \( \in Kerf\), alors on a : \(\left\{ \begin{array}{l} x + y = 0\\ x + y - 2z = 0\\ x + y + z = 0 \end{array} \right.\), soit \(x+y=0\) et \(z=0\)
Ainsi \(\overrightarrow u \left( {x; - x;0} \right) \in Kerf\) dont \(Kerf\) est la droite vectorielle dirigee par le vecteur \(\overrightarrow e \left( {1; - 1;0} \right)\).

PARTIE B : Évaluation des compétences

1. Déterminons à partir de quelle année on comptera plus de 20 000 champignons
Désignons par \({P_n}\) le nombre de champignons après \(n\) années. \({P_0}\) correspond au nombre de champignons en 2022, soit 12000.
On a \({P_{n + 1}} = {P_n} + {P_n} \times \frac{5}{{100}}\) \( = 1,05{P_n}\)
Ainsi \(\left( {{P_n}} \right)\) est une suite géométrique de raison 1,05 , donc \({P_{n + 1}} = 12000{\left( {1,05} \right)^n}\)
\({P_n} \ge 20000\) donne \(n \succ 10,47 = 11\)
Donc en 2023 la production dépassera 20000
2. Déterminons l’aire de ce jardin en période des pluies
L’aire de ce jardin est : \(A = \int\limits_0^{20} {\left[ {4 + \ln \left( {x + 20} \right)} \right]} dx\) \( \times 100da{m^2}\)
En utilisant une intégration par parties sur la recherche d’une primitive de la fonction \({\ln \left( {x + 20} \right)}\),
\(A = [4x + (x + 20)\) \(\ln (x + 20 - x]_0^{20} \approx \) \(119,91ha\)
3. Déterminons le nombre initial de bactéries dans ce laboratoire.
Notons \(P(t)\) le nombre de bactéries à chaque instant \(t\) , \(t\) en heures.
On a \(P'(t) = kP(t)\) ( équation différentielle du premier ordre). Ainsi, \(P(t) = c{e^{kt}}\)
\(\left\{ \begin{array}{l} P(3) = 5 \times {10^8}\\ P(5) = {10^{10}} \end{array} \right.\) nous donne
\(k = \ln \sqrt {20} \) et \(c = \frac{{{{10}^8}}}{{4\sqrt {20} }}\)
\(P(0) = c{e^{0k}} = \) \(c = 5,59 \times {10^6}\)

Présentation 0,5 pt