PARTIE A : ÉVALUATION DES RESSOURCES / 10points

EXERCICE 1 : Vérification des savoirs / 8point

1. Définition :
Un oscillateur harmonique est un oscillateur dont la loi horaire est une fonction sinusoïdale du temps et l’équation différentielle réguisant ses oscillations de la forme \(\ddot x + {\omega _0}x = 0\). 1pt
La radioactivité est une propriété des noyaux atomiques instables de se transformer spontanément en noyaux d’autre espèce avec émission de particules accompagnée de rayonnement électromagnétique. 1pt
Le champ de gravitation est une région de l’espace à l’intérieur duquel tout corps matériel est soumis à une force gravitationnelle. 1 pt
2. Énonçons :
2.1- La loi 2e loi de Newton sur les mouvements : 1 pt
« Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide de masse constante m est égale au produit de la masse par le vecteur accélération \(\overrightarrow {{a_G}} \) de son centre d’inertie. ». \(\sum {{{\overrightarrow F }_{ext}}} = m\overrightarrow {{a_G}} \).
2.2- Énonçons la loi de Laplace : 1 pt
« Une portion de conducteur de longueur \(l\) parcouru par un courant d’intensité \(I\) et placée dans un champ magnétique \(\overrightarrow B \) est soumise à une force électromagnétique \(\overrightarrow F \) dit de Laplace appliquée au milieu de la portion »
3. Écrivons la relation traduisant la loi de décroissance radioactive : 1pt
\(A(t) = {A_0}{e^{ - \lambda t}}\)
Avec \(A(t)\) activité à l’instant \( ?\), \({A_0}\) activité à l’instant initial \(\lambda \) constante radioactive.
4. Répondons par Vrai ou Faux : 2 pts

EXERCICE 2 : Application des savoirs et savoir-faire /8points

A- Grandeurs sinusoïdales :
Déterminons par la construction de Fresnel la grandeur \(?\) telle que \(y = {y_1} + {y_2}\)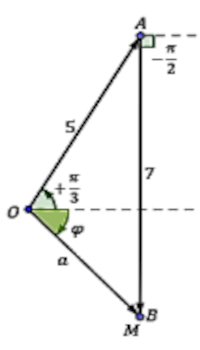
\(\tan \varphi = \) \(\frac{{\left( {{a_1}\sin {\varphi _1} + {a_2}\sin {\varphi _2}} \right)}}{{\left( {{a_1}\cos {\varphi _1} + {a_2}\cos {\varphi _2}} \right)}}\) \( = \frac{{\left( {5\sin \frac{\pi }{3} + 7\sin \left( { - \frac{\pi }{2}} \right)} \right)}}{{\left( {5\cos {\varphi _1} + 7\cos \left( { - \frac{\pi }{2}} \right)} \right)}}\)
\(\varphi = - {46,88^o} = \) \( - 0,818 \)rad
Par ailleurs \(a = \) \(\sqrt {a_1^2 + a_1^2 + 2{a_1}{a_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)} \)
\(a = 6,24\) cm
\(y = 6,24\sin \) \(\left( {100\pi - 0,82} \right)\) en cm

B- Forces électrostatiques :

B.1- Représentons les interactions qui s’exercent entre \({q_A}\) et \({q_B}\) : 1 pt
B.2- Calculons l’intensité de la force que l’un exerce sur l’autre :
D’après la loi de Coulomb on a : \(F = \frac{{K\left| {{q_A}} \right|\left| {{q_B}} \right|}}{{A{B^2}}}\)
\(F = 150N\)

C- Analyse dimensionnelle : 2 pts

Déterminons la dimension de ? : on a :
\(\frac{{{T^2}}}{{{a^3}}} = \frac{{4{\pi ^2}}}{{GMs}} \Rightarrow \) \(G = \frac{{4{\pi ^2}{a^3}}}{{{T^2}Ms}}\).
\(\left[ G \right] = \frac{{\left[ {4{\pi ^2}} \right]{{\left[ a \right]}^3}}}{{{{\left[ T \right]}^2}\left[ {Ms} \right]}}\) \( = {M^{ - 1}}{L^3}{T^{ - 2}}\)

EXERCICE 3 : Utilisation des savoirs et savoir-faire /8points

A- ? = 2?? /?i? et ? = 2,0 ?/???

A.1/ Déterminons la fréquence de ces deux tensions : les deux tensions sont synchrones, ce qui donne d’écrire : \({f_1} = {f_2} = f\). Ainsi on a : \(f = \frac{1}{T}\) or graphiquement \(T = 8b \Rightarrow \) \(f = \frac{1}{{8b}}\) 1 pt
AN : \(f = 62,5Hz\)
A.2/ La tension \({u_2}\) est en avance sur la tension \({u_1}\).
A.3/ Déterminons le déphasage \(\varphi = {\varphi _2} - {\varphi _1}\): le décalage horaire est donné par \(\theta = \frac{{\left| \varphi \right|}}{{2\pi }}T \Rightarrow \) \(\left| \varphi \right| = \frac{{2\pi \theta }}{T}\) or graphiquement \(\theta = 1b \Rightarrow \left| \varphi \right|\) \( = \frac{{2\pi 1 \times b}}{{8b}}\)
Il vient \(\left| \varphi \right| = \frac{\pi }{4}\) et comme la tension \({u_1}\) est en retard de phase sur la tension \({u_2}\) alors \({\varphi = {\varphi _2} - {\varphi _1} \prec 0}\). Donc \(\varphi = - \frac{\pi }{4}\)
A.4/ Ecrivons les équations horaires de \({u_1}\) et \({u_2}\) pour \({{\varphi _1} = 0}\):
On a : \({u_1} = {U_{1m}}\sin \left( {2\pi ft + {\varphi _1}} \right)\) et \({u_1} = {U_{2m}}\sin \left( {2\pi ft + {\varphi _2}} \right)\)
Or graphiquement on a : \({U_{1m}} = 3s = 6V\) et \({U_{2m}} = 2s = 4V\)
Par ailleurs \({\varphi = {\varphi _2} - {\varphi _1}}\) \({ = - \frac{\pi }{4}}\) \({ \Rightarrow {\varphi _2} = \frac{\pi }{4}}\) et \({\varphi _1} = 0\)
Ainsi \({u_1} = 6\sin \left( {125\pi t} \right)\) et \({u_2} = 6\sin \left( {125\pi t + \frac{\pi }{4}} \right)\)

B/ Radioactivité :

B.1/ Écrivons l’équation-bilan de désintégration :
\({}_{84}^{210}Po \to {}_{82}^{206}Pb + {}_2^5He\)
B.2/Calculons en ??? , l’énergie libérée au cours de cette désintégration :
\(E = |m({}_{84}^{210}Po) - \) \(m({}_{82}^{206}Pb) - m({}_2^5He)| \times {c^2}\)
AN: \(E = 5,41MeV\)

PARTIE B : ÉVALUATION DES COMPÉTENCES / 16points

Tache 1 8 pts
Déterminons si OBAM pourra épouser MENGUE :
Problème : déterminer si OBAM pourra atteindre le singe avec sa flèche.
Démarche : appliquer le TCI pour déterminer la valeur de la portée, la comparer à la distance ? et conclure.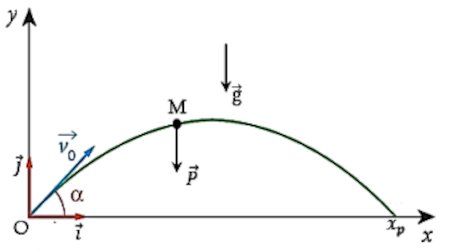
D’après le théorème du centre d’inertie, on a : \(\sum {{{\overrightarrow F }_{ext}}} = m{\overrightarrow a _G}\) \( \Rightarrow \overrightarrow P = m{\overrightarrow a _G}\) \( \Leftrightarrow \overrightarrow g = {\overrightarrow a _G}\)
Or \(\overrightarrow g \left| \begin{array}{l} 0\\ - g \end{array} \right. \Leftrightarrow {\overrightarrow a _G}\left| \begin{array}{l} 0\\ - g \end{array} \right.\)
\({\overrightarrow a _G}\left| \begin{array}{l} 0\\ - g \end{array} \right. \Rightarrow \) \(\overrightarrow V \left| \begin{array}{l} Vo\cos \alpha \\ - gt + Vo\sin \alpha \end{array} \right.\) \( \Rightarrow \overrightarrow {OM} \) \(\left| \begin{array}{l}
x = \left( {Vo\cos \alpha } \right)t\\ y = \frac{1}{2}g{t^2} + \left( {Vo\sin \alpha } \right)t \end{array} \right.\) car \(\overrightarrow {{V_0}} \left| \begin{array}{l} Vo\cos \alpha \\ Vo\sin \alpha \end{array} \right.\)
L’équation de la trajectoire donne :
\(y = - \frac{g}{{2V_o^2{{\cos }^2}\alpha }}{x^2}\) \( + x\tan \alpha \)
La portée est donnée pour\({y_p} = 0\) et \({x_p} = \frac{{V_0^2\sin 2\alpha }}{g}\) soit \({x_p} = 62,5\) m
Conclusion : On constate que \({x_p} \prec L\), ça veut dire que peu importe le mouvement du singe la flèche ne va pas l’atteindre. Par conséquent OBAM ne pourra pas épouser
MENGUE.

Tache 2  8 pts
Prononçons-nous sur la date approximative de l'éruption :
Il suffit d’exploiter la loi de décroissance radioactive des noyaux de \({}_{19}^{40}K\) et sa période radioactive pour déterminer le date de l’éruption.
On sait à un instant \(?\) le nombre de noyau \({}_{19}^{40}K\)présent est donnée par : \(N(K) = {N_o}(K){e^{ - \lambda t}}\)
Or au cours du temps l’argon \({}_{18}^{40}Ar\) se forme par captation électronique du \({}_{19}^{40}K\) suivant l’équation :
\({}_{18}^{40}Ar + {}_{ - 1}^0e \to {}_{18}^{40}Ar\)
On peut donc écrire :
\(N(K) = {N_o}(K) + \) \(N(Ar) \Rightarrow N(Ar)\) \( = {N_o}(K) - N(K)\)
\(N(Ar) = {N_o}(K)\) \(\left( {1 - {e^{ - \lambda t}}} \right)\)
Par ailleurs :
\(\frac{{N(Ar)}}{{N(K)}} = \) \(\frac{{{N_o}(K)\left( {1 - {e^{ - \lambda t}}} \right)}}{{{N_o}(K){e^{ - \lambda t}}}}\) \( = - 1 + {e^{\lambda t}}\)
\(N(Ar) = \frac{{{m_{Ar}} \times \eta }}{{{M_{Ar}}}}\) et \(N(K) = \frac{{{m_{K}} \times \eta }}{{{M_{Ar}}}}\)
\(\frac{{N(Ar)}}{{N(K)}} = \frac{{\frac{{{m_{Ar}} \times \eta }}{{{M_{Ar}}}}}}{{\frac{{{m_K} \times \eta }}{{{M_K}}}}}\) \( = \frac{{{m_{Ar}} \times {M_K}}}{{{m_K} \times {M_{Ar}}}} = - 1 + {e^{\lambda t}}\)
\({e^{\lambda t}} = 1 + \frac{{{m_{Ar}} \times {M_K}}}{{{m_K} \times {M_{Ar}}}}\) \( \Rightarrow t = \frac{1}{\lambda }\ln \) \(\left( {1 + \frac{{{m_{Ar}} \times {M_K}}}{{{m_K} \times {M_{Ar}}}}} \right)\) avec \(\lambda = \frac{{\ln 2}}{T}\)
AN : \(t = 2,72 \times {10^7}\) ans
Conclusion : L’âge approximative de l’éruption est \(t = 2,72 \times {10^7}\) ???

Correction proposée par M. MBELE SOUMAN Nestor e-mail :