Partie I : Évaluation des ressources / 24 pts
Exercice 1 : Vérification des savoirs / 8 pts
1.1 Définir :
Coefficient d’atténuation linéique du rayonnement : c’est un coefficient qui décrit la diminution d’intensité d’un rayonnement qui traverse un milieu en fonction de l’énergie de ce rayonnement. 1 pt
Activité d’une source radioactive : c’est le nombre de désintégration par seconde. 1 pt
1.2 Énoncés
Principe de superposition de petits mouvements : « Lorsque plusieurs ondes de faibles amplitudes se propageant dans la même direction et dans un même milieu se rencontrent, l’élongation résultante est égale à la somme algébrique des élongations de chacune des ondes » 1 pt
Troisième loi de Newton : « Lorsqu’un corps A exerce sur un corps B une force \({\overrightarrow F _{A/B}}\) simultanément le corps B exerce sur A une force \({\overrightarrow F _{B/A}}\) de même direction, de même intensité et de sens contraire » 1pt
1.3 Description par un schéma légendé du phénomène de diffraction de la lumière : 1 pt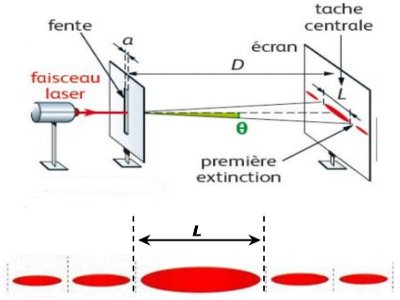 1.4 Formule de l’interfrange : \(i = \frac{{\lambda D}}{a}\)
1.4 Formule de l’interfrange : \(i = \frac{{\lambda D}}{a}\)
Explicitons les grandeurs :
\(\lambda \) longueur d’onde de la radiation utilisée
\(a\) distance entre les fentes secondaires \({F_1}\) et \({F_1}\)
\(D\) distance qui sépare les fentes secondaires et l’écran
1.5 Répondre par vrai ou faux 1 pt x 2 =2p
i) faux
ii) Faux
Exercice 2 : Application des savoirs / 8 pts
2-1 Effet photoélectrique / 3 pts
2.1.1 Longueur d’onde seuil du métal de tungstène :
\({W_0} = \frac{{hC}}{{{\lambda _0}}}\) \( \Rightarrow {\lambda _0} = \frac{{hC}}{{{W_0}}}\) 0,75 pt
AN : \({\lambda _0} = 1,728 \times {10^{ - 7}}\) m 0,75 pt
2.1.2 Calcul de \({E_{{C_{\max }}}}\)
\(W = {E_{{C_{\max }}}} + \) \({W_0} \Rightarrow {E_{{C_{\max }}}} = \) \(W - {W_0} = \frac{{hC}}{\lambda }\) \( - {W_0}\) 0,75 pt
AN : \({E_{{C_{\max }}}} = \) \(7,184 \times {10^{ - 19}}\) J 0,75 pt
2.2 Courant alternatif / 3pts
2.2.1 Déterminons l’impédance du circuit
\(Z = \sqrt {{R^2} + {{\left( {L\omega } \right)}^2}} \) 0,75 pt
AN : \(Z = \) \(\sqrt {{{100}^2} + {{\left( {0,100x100} \right)}^2}} \) \( = 100,5\Omega \) 0,75 pt
2.2.2 Construction de Fresnel pour représenter la tension efficace aux bornes du circuit 1,5 pt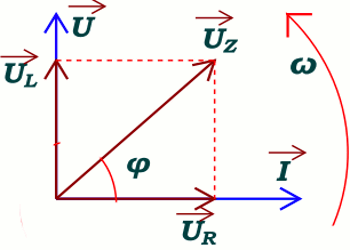 2.3 Champ électrostatique
2.3 Champ électrostatique
2.3 Déterminons l’intensité de \({\overrightarrow E _{O/M}}\)
\({E_{O/M}} = \frac{{k\left| q \right|}}{{O{M^2}}}\) 1 pt
AN : \({E_{O/M}} = 1,72 \times {10^5}\) N/C 1 pt
Exercice 3 : Utilisation des savoirs
A-Uniquement la série TI / 8pts
A.1. Radioactivité
Déterminons en Mev l’énergie moyenne de liaison par nucléon du noyau de \({}_6^{14}C\)
\(\varepsilon = \frac{{{E_l}}}{A}\) 0,5 pt
Calcul de l’énergie de liaison
\({E_l} = \Delta m{C^2}\) \( = [Z{m_p} + (A - Z){m_n}\) \( - m({}_6^{14}C)]{C^2}\) 0,5 pt
AN : \({E_l} = 70,2592\)Mev 0,5 pt
Calcul de l’énergie moyenne de liaison par nucléon
\(\varepsilon = \frac{{{E_l}}}{A}\) 0,5 pt
AN : \(\varepsilon = \frac{{70,2592}}{{14}}\) \( = 5,018\) Mev 0,5 pt
A.1.2 Equation de désintégration de \({}_6^{14}C\)
\(_6^{14}C \to {}_{ - 1}^0e\) \( + {}_x^yX + E\) 1 pt
D’après les lois de conservation de SODDY on a : \(\left\{ \begin{array}{l}x = 14\\y = 7\end{array} \right.\) 1 pt
A.2 Stroboscopie
Déterminons la plus grande fréquence des éclairs pour laquelle le disque parait immobile avec un rayon blanc
\(N = 24Hz\) et \(10 \le Ne \le 50\)
Posons \(N = kNe\) avec \(k \in {N^*}\) ainsi \(10 \le \frac{N}{k} \le 50\) \( \Rightarrow 0,48 \le k\) \( \le 2,4\)
• Les valeurs de k pour lesquelles on observe l’immobilité apparente du disque sont k=1 et k=2
• La valeur de la plus grande fréquence des éclairs pour laquelle le disque parait immobile avec un rayon est \(Ne = kN\) \( = 1 \times 24 = 24\) Hz 1 pt
A.3 Construction de Fresnel
\({x_1}(t) = \) \(4\cos (100\pi t)\) cm et \({x_2}(t) = 4\) \(\cos (100\pi t + \frac{\pi }{4})\) cm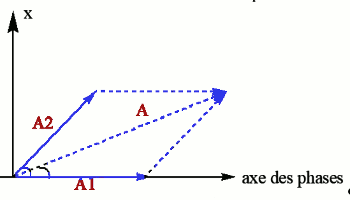 L’élongation résultante sera de la forme \(x(t) = A\) \(\cos (100\pi t + \varphi )\)
L’élongation résultante sera de la forme \(x(t) = A\) \(\cos (100\pi t + \varphi )\)
Ainsi, d’après la formule démontrer dans le cours
\(A = \) \(\sqrt {{4^2} + {4^2} + 24.4\cos \frac{\pi }{4}} \) \( = 7,39\) cm 0,5 pt
\(\tan \varphi = \) \(\frac{{4\sin 0 + 4\sin \frac{\pi }{4}}}{{4\cos 0 + 4\cos \frac{\pi }{4}}}\) \( = 0,4142\)
\(\varphi = {22,49^o}\) \( = 0,12\pi \) 0,5 pt
\(x(t) = 7,39\cos \) \(\left( {100\pi + 0,12\pi } \right)\) en cm 0,5 pt
B-Uniquement la série D / 8pts
B.1. Réaction de fusion nucléaire
B.1.1 Identification de la particule X
\({}_1^2H + {}_1^3H \to \) \({}_2^4He + {}_Z^AX\) \( + \gamma \) 0,5 pt
En utilisant les lois de conservations de SODDY, on a : \(2 + 3 = \) \(4 + A\) et \(1 + 1 = \) \(2 + Z\)
soit A=1 et Z= 0 d’où l’élément X est un neutron
\({}_1^2H + {}_1^3H \to \) \({}_2^4He + {}_0^1n\) \( + \gamma \) 0,5 pt
B.1.2 Énergie produite par cette réaction
\(E = \left| {\Delta m} \right|{C^2}\) \( = |{m_{reactifs}} - \) \({m_{produits}}|{C^2}\) 1 pt
AN : \(E = 1,49 \times {10^{ - 10}}\) J 1 pt
B.2. Pendule simple
B.2.1. Mode opératoire permettant de déterminer la période d’un pendule simple.
Après avoir monté le dispositif constitué d’un support, d’un solide s de masse m, de dimensions négligeables et d’un fil inextensible de longueur L et de masse négligeable.
On écarte l’ensemble (solide + fil) de la position d’équilibre d’un angle \(\theta \) petit qu’on mesure à l’aide d’un rapporteur puis on abandonne le système sans vitesse initiale. On compte n oscillations ainsi que la durée totale(t) de ces oscillations à l’aide d’un chronomètre. En posant t=nT on déduit la période (T) du pendule ainsi constitué. 2 pts
B.2.2. Calcul de la longueur de ce pendule
\(T = 2\pi \sqrt {\frac{L}{g}} \) \( \Rightarrow L = \frac{{{T^2}g}}{{4{\pi ^2}}}\) 0,5 pt
AN : \(L = 0,98\) m 0,5 pt
B.2.3. Tension du fil au passage par la position d’équilibre
D’après le TCI \(\overrightarrow T + \overrightarrow P = m{\overrightarrow a _G}\)
En projetant suivant la normale passant par le centre de rotation (point d’accroche du fil), nous avons
\(T = mg + m{a_n}\) \( = m\left( {g + \frac{{{V^2}}}{L}} \right)\) avec \({V^2} = \) \(2gL\left( {1 - \cos \theta } \right)\), nous avons après substitution
\(T = mg\) \(\left( {3 - 2\cos \theta } \right)\) 0,5 pt +0,5 pt
AN : \(T = 0,62\) N
II Évaluation des compétences
Situation problème :
Données : VA=260m/s, g=9,8m/s, \({10^o} \le \theta \le {90^o}\), V0=36km/h, \(\left\{ \begin{array}{l}{y_A} = 3,30km\\{x_A} = 9,40km\end{array} \right.\)
1. Utilisons un raisonnement scientifique et les données pour proposer au chef de village la distance minimale de sécurité à observer par les populations
a) Établissons d’abord les équations horaires du mouvement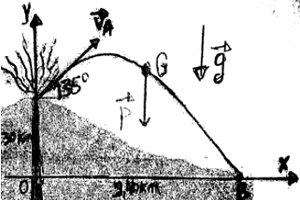 1 pt
1 pt
En appliquant le TCI à une particule de masse m dans un référentiel de laboratoire supposé galiléen, on a : \({\overrightarrow a _G} = \overrightarrow g \)
Ainsi \(\overrightarrow {OM} \left| \begin{array}{l}x\\y\end{array} \right.\) avec \(x(t) = \) \(\left( {{V_0}\cos \alpha } \right)t\) \( + {x_A}\) et \(y(t) = - \frac{1}{2}g{t^2}\) \( + {V_0}\sin \alpha t + {y_A}\) 1 pt
b) Équation de la trajectoire 1 pt
\(y = - \frac{1}{2}\frac{g}{{V_0^2{{\cos }^2}\alpha }}{x^2}\) \( + x\tan \alpha + {y_A}\)
c) Expression de la portée
Au sol y=yA soit \({x_P} = \) \(\frac{{V_0^2\sin 2\alpha }}{g}\)
d) calcul de la portée minimale
Pour \(\alpha = {10^o}\) la portée d’une particule est minimale
AN : \({x_P} = \) \(\frac{{{{260}^2}\sin {{20}^o}}}{{9,8}}\) \( = 2,35\) Km
On conclut que la distance minimale de sécurité à observer par la population est à d=2,36 km du pied du volcan.
2. En exploitant les informations, examinons si le touriste s’échappera en tout sécurité
a) calculons la portée d’une particule pour \(\alpha = {35^o}\)
\({x_P} = \frac{{{{260}^2}\sin {{70}^o}}}{{9,8}}\) \( = 6,48\) km
b) Comparons cette portée à la distance où se trouve le touriste soit X la position du touriste au moment où il entend le bruit. On a \(X = 9400 - \) \(30 = 9,37\) km
c) conclusion : comme la portée de la particule chaude est inférieure à la position du touriste, il s’échappera en toute sécurité


