I. Lieux géométriques
Le lieu géométrique est un ensemble de points d’un espace géométrique qui jouissent d’une propriété métrique commune.
I.1 Distance entre deux points A et B
Soient A et B, deux points d'affixes respectives \({Z_A}\) et \({Z_b}\) .
\(d\left( {A,B} \right) = \) \(\left\| {\overrightarrow {AB} } \right\| = \) \(\left| {{Z_B} - {Z_A}} \right|\)
I.2 Cercle de centre A et de rayon r
Soit \(M\left( \begin{array}{l}x\\y\end{array} \right)\) d'affixe \({Z_M}\). A d'affixe\({Z_A}\).
\(d\left( {A,M} \right) = \) \(\left| {{Z_M} - {Z_A}} \right| = r\)
I.3 Médiatrice d'un segment
Soit \(M\left( \begin{array}{l} x\\y\end{array} \right)\) d'affixe \({Z_M}\); A d'affixe \({Z_A}\) et B d'affixe \({Z_B}\) .
M appartient à la médiatrice du segment \(\left[ {AB} \right]\)
\(d\left( {A,M} \right) = \) \(d\left( {A,M} \right) \Leftrightarrow \) \(\left| {{Z_M} - {Z_A}} \right| = \) \(\left| {{Z_M} - {Z_B}} \right|\)
I.4 Droite passant par un point A et faisant un angle \(\alpha \) avec l’horizontale
Soit \(M\left( \begin{array}{l} x\\y\end{array} \right)\) d'affixe \({Z_M}\); A un point d'affixe\({Z_A}\); et ( D ) une droite du plan. ( D ) passe par A et fait un angle\(\alpha \) avec l’horizontale si \(\arg \left( {{Z_M} - {Z_A}} \right)\) \( = \alpha + k\pi \)
II. Écritures complexes et transformations du plan
II.1. Définition de transformation du plan et d’écriture complexe
Le plan complexe est muni d’un repère orthonormé direct \(\left( {O,I,J} \right)\).
• Une transformation du plan est une application bijective du plan dans le plan.
• Soit F une transformation du plan qui à tout point M associe le point M’. L’application bijective \(f\) de \( \mathbb{C}\) dans \( \mathbb{C}\) qui à l’affixe \(Z\) de M, associe l’affixe \(Z’\) de M’ s’appelle la transformation complexe associée à F.
L’application F s’appelle la transformation ponctuelle associée à \(f\)
• L’expression de \(Z’\) en fonction de \(Z\) s’appelle l’écriture complexe de F
II.2. Écritures complexes de symétrie centrale de centre O et de symétries
Le plan complexe est muni d’un repère orthonormé direct (O, I, J).
• La symétrie orthogonale d'axe (OI) a pour écriture complexe : \(Z' = \overline Z \).
• La symétrie centrale de centre O a pour écriture complexe : \(Z' = - Z\).
• La symétrie orthogonale d'axe (OJ) a pour écriture complexe : \(Z' = - \overline Z \)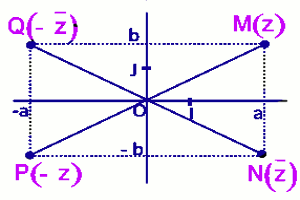
II.3. Écriture complexe d’une translation, d’une homothétie et d’une rotation
II.3.1 Translation
\({t_{\overrightarrow u }}\) est la translation de vecteur \(_{\overrightarrow u }\) d'affixe b. M et M' sont les points du plan d'affixes respectives \(Z\) et \(Z’\).
On a \(M' = {t_{\overrightarrow u }}\left( M \right)\) \( \Leftrightarrow \overrightarrow {MM'} = \overrightarrow u \) \( \Rightarrow Z' - \) \(Z = b\)
Soit \(Z' = Z + b\)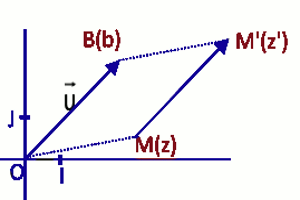
La translation de vecteur \(\overrightarrow u \) d’affixe \(b\) a pour écriture complexe : \(Z' = Z + b\)
II.3.2 Homothétie de centre \(\Omega \) et de rapport \(?\), avec \(k \in \) \( \mathbb{R^*}\)
\(h\) est l'homothétie de centre \(\Omega \) d’affixe \({Z_\Omega }\) et de rapport\(?\), avec \(k \in \) \( \mathbb{R^*}\).
\(M\) et \(M'\) sont les points du plan d'affixes respectives \(Z\) et \(Z’\). On a :
\(M = h\left( {M'} \right)\) \( \Leftrightarrow \overrightarrow {\Omega M'} = \) \(k\overrightarrow {\Omega M} \)
\( \Leftrightarrow Z' - {Z_\Omega }\) \( = k\left( {Z - {Z_\Omega }} \right)\)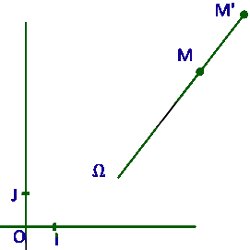
L'homothétie de centre \(\Omega \) d’affixe \({Z_\Omega }\) et de rapport \(k\) a pour écriture complexe \(Z' = \) \(k\left( {Z - {Z_\Omega }} \right)\) \( + {Z_\Omega }\)
II.3.3 Rotation de centre Ω et d’angle \(\theta \), avec \(\theta \in \left] { - \pi ,\pi } \right]\)
r est la rotation de centre de centre \(\Omega \) d’affixe \({Z_\Omega }\) et d'angle orienté de mesure principale \(\theta \).
• \(M\) et \(M'\) sont les points du plan d'affixes respectives \(Z\) et \(Z’\) tels que M est distinct de \(\Omega \). On a :
\(M' = r\left( M \right)\) \( \Rightarrow \) \(\left\{ \begin{array}{l}\Omega M' = \Omega M\\mes\left( {\widehat {\overrightarrow {\Omega M} ;\overrightarrow {\Omega M'} }} \right) = \theta \end{array} \right.\)
• \(r\left( \Omega \right) = \Omega \)
On a :
\(\frac{{Z' - {Z_\Omega }}}{{Z - {Z_\Omega }}}\) \( = {e^{i\theta }} \Rightarrow \) \(Z' = {e^{i\theta }}\) \(\left( {Z - {Z_\Omega }} \right) + {Z_\Omega }\)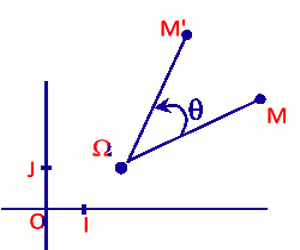
La rotation de centre \(\Omega \) d’affixe \({{Z_\Omega }}\) et d'angle orienté de mesure principale \(\theta \) a pour écriture complexe : \(Z' = {e^{i\theta }}\left( {Z - {Z_\Omega }} \right)\) \( + {Z_\Omega }\)
Tableau récapitulatif des écritures complexes des transformations usuelles


