En mathématique, la trigonométrie est l’application du calcul à la détermination des mesures des angles et des côtés des triangles.
I. Les valeurs remarquables des angles
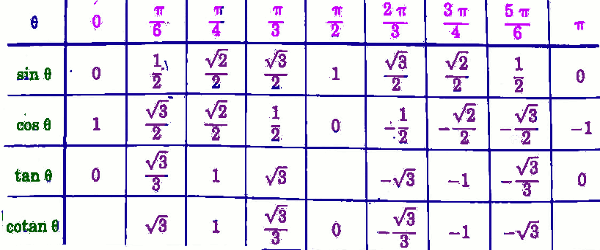
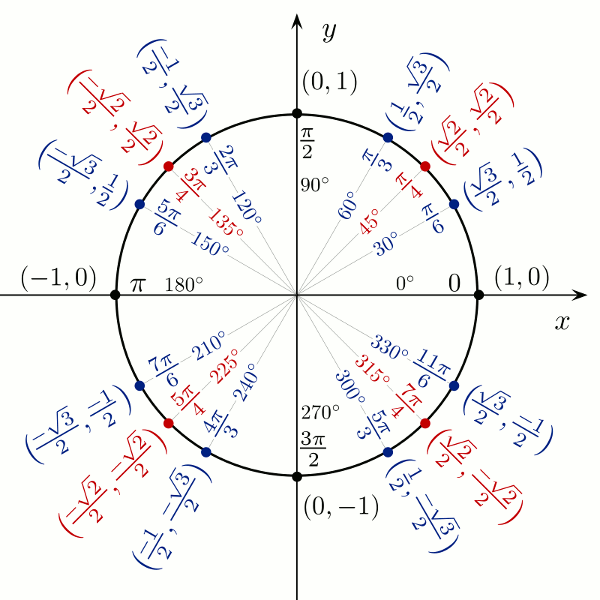
II. Principales relations trigonométriques
La notation \({\theta _1} = {\theta _2}\) \(\left[ \alpha \right]\) signifie que \({\theta _1} = {\theta _2}\) \( + k\alpha \)
II.1 Formulaires
Pour \(\theta \ne \frac{\pi }{2}\left[ \pi \right]\), \(\tan \theta = \) \(\tan \theta = \) \(\frac{{\sin \theta }}{{\cos \theta }}\)
Pour tout \(\theta \ne 0\left[ \pi \right]\), \(\cot an\theta = \) \(\frac{{\cos \theta }}{{\sin \theta }}\)
Pour tout \(\theta \ne 0\left[ {\frac{\pi }{2}} \right]\), \(\tan \theta = \) \(\frac{1}{{\cot an\theta }}\) et \(\cot an\theta = \) \(\frac{1}{{\tan \theta }}\)
Pour tout \(\theta \), \({\cos ^2}\theta + \) \({\sin ^2}\theta = 1\)
Pour tout \(\theta \ne \frac{\pi }{2}\left[ \pi \right]\), \(1 + {\tan ^2}\theta \) \( = \frac{1}{{{{\cos }^2}\theta }}\)
Pour tout \(\theta \ne 0\left[ \pi \right]\), \(1 + \cot a{n^2}\theta \) \( = \frac{1}{{{{\sin }^2}\theta }}\)
La fonction sinus est une fonction impaire donc \(\sin \left( { - \theta } \right) = \) \( - \sin \left( \theta \right)\)
La fonction cosinus est une fonction paire donc \(\cos \left( { - \theta } \right) = \) \(\cos \left( \theta \right)\)
• \(\tan \left( { - \theta } \right) = \) \( - \tan \left( \theta \right)\)
• \(\cot an\left( { - \theta } \right) = \) \( - \cot an\left( \theta \right)\)
• \(\sin \left( {\theta + \pi } \right)\) \( = - \sin \left( \theta \right)\)
• \(\cos \left( {\theta + \pi } \right) = \) \( - \cos \left( \theta \right)\)
• \(\tan \left( {\theta + \pi } \right) = \) \(\tan \left( \theta \right)\)
• \(\cot an\left( {\theta + \pi } \right)\) \( = \cot an\left( \theta \right)\)
• \(\sin \left( {\pi - \theta } \right)\) \( = \sin \left( \theta \right)\)
• \(\cos \left( {\pi - \theta } \right) = \) \( - \cos \left( \theta \right)\)
• \(\tan \left( {\pi - \theta } \right) = \) \( - \tan \left( \theta \right)\)
• \(\cot an\left( {\pi - \theta } \right) = \) \( - \cot an\left( \theta \right)\)
• \(\sin \left( {\theta + \frac{\pi }{2}} \right)\) \( = \cos \left( \theta \right)\)
• \(\cos \left( {\theta + \frac{\pi }{2}} \right) = \) \( - \sin \left( \theta \right)\)
• \(\tan \left( {\theta + \frac{\pi }{2}} \right) = \) \( - \cot an\left( \theta \right)\)
• \(\cot an\left( {\theta + \frac{\pi }{2}} \right)\) \( = - \tan \left( \theta \right)\)
• \(\sin \left( {\frac{\pi }{2} - \theta } \right)\) \( = \cos \left( \theta \right)\)
• \(\cos \left( {\frac{\pi }{2} - \theta } \right)\) \( = \sin \left( \theta \right)\)
• \(\tan \left( {\frac{\pi }{2} - \theta } \right)\) \( = \cot an\left( \theta \right)\)
• \(\cot an\left( {\frac{\pi }{2} - \theta } \right)\) \( = \tan \left( \theta \right)\)
II.2 Formules d’addition
• \(\cos \left( {\theta + \theta '} \right) = \) \(\cos \theta \cos \theta ' - \) \(\sin \theta \sin \theta '\)
Si \(\theta = \theta '\)
• \(\cos \left( {\theta + \theta '} \right) = \) \(\cos \left( {2\theta } \right) = \) \({\cos ^2}\theta - {\sin ^2}\theta \)
• \(\cos \left( {\theta - \theta '} \right) = \) \(\cos \theta \cos \theta ' + \) \(\sin \theta \sin \theta '\)
• \(\sin \left( {\theta + \theta '} \right) = \) \(\sin \theta \cos \theta ' + \) \(\cos \theta \sin \theta '\)
• \(\sin \left( {\theta - \theta '} \right) = \) \(\sin \theta \cos \theta ' - \) \(\cos \theta \sin \theta '\)
• \(\tan \left( {\theta + \theta '} \right) = \) \(\frac{{\tan \theta + \tan \theta '}}{{1 - \tan \theta \tan \theta '}}\)
• \(\tan \left( {\theta - \theta '} \right) = \) \(\frac{{\tan \theta - \tan \theta '}}{{1 + \tan \theta \tan \theta '}}\)
III. Équations trigonométriques
Etant donnée \(\alpha \) réel, les solutions de l’équation
\(x \in \) \( \mathbb{Z}\), \(\sin x = \sin \alpha \) est telle que :
\(\left\{ \begin{array}{l} x = \alpha + 2k\pi \\x = \pi - \alpha + 2k\pi \end{array} \right.\) avec
\(x \in \) \( \mathbb{Z}\), \(\cos x = \cos \alpha \) est telle que :
\(\left\{ \begin{array}{l}x = \alpha + 2k\pi \\x = - \alpha + 2k\pi \end{array} \right.\)
Etant donnée \(\alpha \) réel, diffèrent de \(\frac{\pi }{2}\left[ \pi \right]\), les solutions de l’équation, les solutions de l’équation
\(x \in \) \( \mathbb{R}\), \(\tan x = \tan \alpha \) avec \(x = \alpha + k\pi \) \(k \in \) \( \mathbb{Z}\),
IV Transformation de somme et produit
Étant donnés p et q deux réels :
• \(\cos p + \cos q\) \( = 2\cos \frac{{p + q}}{2}\) \(\cos \frac{{p - q}}{2}\)
• \(\cos p - \cos q\) \( = - 2\sin \frac{{p + q}}{2}\) \(\sin \frac{{p - q}}{2}\)
• \(\sin p + \sin q\) \( = 2\sin \frac{{p + q}}{2}\) \(\cos \frac{{p - q}}{2}\)
• \(\sin p - \sin q\) \( = 2\sin \frac{{p - q}}{2}\) \(\cos \frac{{p + q}}{2}\)
IV.1 Linearisation
• \(\sin \theta \cos \theta ' = \) \(\frac{1}{2}(\sin \left( {\theta + \theta '} \right) + \) \(\sin \left( {\theta - \theta '} \right))\)
• \(\sin \theta \sin \theta ' = \) \(\frac{1}{2}(\cos \left( {\theta - \theta '} \right)\) \( - \cos \left( {\theta + \theta '} \right))\)
• \(\cos \theta \cos \theta ' = \) \(\frac{1}{2}(\cos \left( {\theta - \theta '} \right) + \) \(\cos \left( {\theta + \theta '} \right))\)
IV.2 Tangente de l’angle moitié
Pour tout \(\alpha \ne \pi \left[ {2\pi } \right]\), \(\alpha \ne \frac{\pi }{2}\left[ \pi \right]\), en posant \(t = \tan \frac{\alpha }{2}\),
\(\tan \alpha = \) \(\frac{{2t}}{{1 - {t^2}}}\)
Pour tout \(\alpha \ne \pi \left[ {2\pi } \right]\), en posant \(t = \tan \frac{\alpha }{2}\),
• \(\sin \alpha = \) \(\frac{{2t}}{{1 + {t^2}}}\)
• \(\cos \alpha = \) \(\frac{{1 - {t^2}}}{{1 + {t^2}}}\)

