Soient Z et Z’ deux nombres complexes tels que : \(Z = a + ib\) et \(Z' = a' + ib'\)
1) Égalité de deux nombres complexes
Deux nombres complexe Z et Z’ sont égaux si et seulement si
\(Z = Z' \Leftrightarrow \) \(a + ib = \) \(a' + ib' \Rightarrow \) \(\left\{ \begin{array}{l}{\mathop{\rm Re}\nolimits} (Z) = {\mathop{\rm Re}\nolimits} (Z')\\{\mathop{\rm Im}\nolimits} (Z) = {\mathop{\rm Im}\nolimits} (Z')\end{array} \right.\)
Soit \(\left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\)
2) Somme de deux nombres complexes
La somme des deux complexes Z et Z’ est le complexe Z’’ tel que :
\(Z'' = Z + Z'\) \( = a + ib + \) \(a' + ib' = \) \((a + a') + \) \(i(b + b')\)
3) Produit de deux nombres complexes
Le Produit des deux complexes Z et Z’ est un nombre complexe Z’’ tel que :
\(Z'' = Z \times Z'\) \( = \left( {a + ib} \right) \times \) \(\left( {a' + ib'} \right) = \) \((aa' - bb') + \) \(i(ab' + a'b)\) avec \({i^2} = - 1\)
4) Le conjugué d’un nombre complexe
Le conjugué d’un nombre complexe \(Z = a + ib\) un nombre complexe noté \(\overline Z \) tel que \(\overline Z = a - ib\)
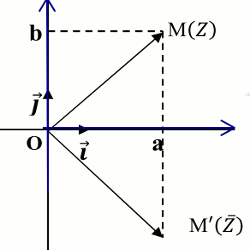
NB : les images des deux nombres complexes \(Z\) et \({\overline Z }\) sont symétriques par rapport à l’axe des réels.
5) Quotient de deux nombres complexes
Le quotient de deux nombres complexes Z et Z’ est un nombre complexe Z’’ tel que :
\(Z'' = \) \(\frac{Z}{{Z'}} = \) \(\frac{{Z\overline {Z'} }}{{Z\overline {Z'} }} = \) \(\frac{{\left( {a + ib} \right)\left( {a' - ib'} \right)}}{{\left( {a' + ib'} \right)\left( {a' - ib'} \right)}}\) \( = \) \(\frac{{aa' + bb'}}{{{{\left( {a'} \right)}^2} + {{\left( {b'} \right)}^2}}} + \) \(i\frac{{ab' - ab'}}{{{{\left( {a'} \right)}^2} + {{\left( {b'} \right)}^2}}}\)
N.B : Le nombre \(\frac{1}{Z}\) est appelé inverse du complexe \(Z\) tel que :
\(\frac{1}{Z} = \) \(\frac{{\overline Z }}{{Z\overline Z }} = \) \(\frac{{\left( {a - ib} \right)}}{{\left( {a + ib} \right)\left( {a - ib} \right)}}\) \( = \frac{{a - ib}}{{{a^2} + {b^2}}}\)
6) Quelques propriétés sur les nombres complexes
Soient deux nombres complexes Z et Z’
P.1 \(Z = \overline Z \Rightarrow Z\) est un reel
P.2 \(Z = - \overline Z \Rightarrow Z\) Eest un imaginaire pur
P.3 \(\overline {Z + Z'} = \) \(\overline Z + \overline {Z'} \)
P.4 \(\overline {Z \times Z'} = \) \(\overline Z \times \overline {Z'} \)
P.5 \(\overline {\left( {\frac{Z}{{Z'}}} \right)} = \frac{{\overline Z }}{{\overline {Z'} }}\)
P.6 \(\overline {\left( {\frac{a}{{Z'}}} \right)} = \frac{a}{{\overline {Z'} }}\) avec \({Z' \ne 0}\)
P.7 \(\overline {{Z^n}} = {\left( {\overline Z } \right)^n}\)
P.8. \({\mathop{\rm Re}\nolimits} (Z) = \) \(\frac{{Z + \overline Z }}{2}\)
P.9 \({\mathop{\rm Im}\nolimits} (Z) = \) \(\frac{{Z - \overline Z }}{2}\)
P.10 \(Z \times \overline Z \) est un réel positif

