Première
C & E & D & TI
Physique
Correction exercice
Bonjour ! Notre page Facebook, la suivre pour nos prochaines publications
Exercice I
1 Montrons que le nouveau rayon réfléchi IR i.e. OS2 tourne d’un angle \(2\alpha \).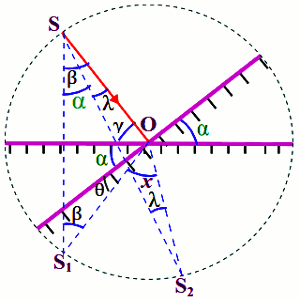
Considérons:

Considérons:
- Le triangle SOS1
\(\beta + \beta + \theta + \alpha + \gamma = \pi {\rm{ }}(1)\)
- Le triangle SOS2
\(2\lambda + x + \theta + \gamma = \pi {\rm{ (2)}}\)
\((1) \Leftrightarrow (2) \Rightarrow 2(\beta - \lambda ) = x\)
Au point S: \(\beta = \alpha + \lambda \Rightarrow \alpha = \beta - \lambda \)
\(x = 2\alpha \)
On constate que lorsque le miroir tourne d’un angle \(\alpha \), l’image tourne de \(2\alpha \) dans le même sens que le miroir.
2 Supposons que la vitesse angulaire du rayon réfléchi est \(\omega '\) , de la relation \(x = 2\alpha {\rm{ }}\) , on a: \(\frac{x}{t} = 2\frac{\alpha }{t}\), soit: \(\omega ' = 2\omega \).
Le rayon réfléchi tourne deux fois plus vite que le miroir.
Exercice II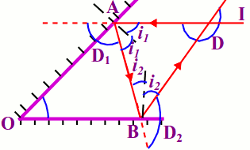

La déviation que produit le premier miroir sur le rayon incident IA:
\({D_1} = \pi - 2{i_i} = \pi - 2{i_1}\)
La déviation que produit le deuxième miroir sur le rayon AB est:
\({D_2} = \pi - 2{i_2}\)
La déviation totale sera donc:
\(D = {D_1} + {D_2}\) \( = 2\pi - 2\left( {{i_1} + {i_2}} \right)\)
Considérons le triangle OAB
\(\alpha + \left( {\frac{\pi }{2} - {i_1}} \right)\) \( + \left( {\frac{\pi }{2} - {i_2}} \right) = \pi \) \(\alpha = {i_1} + {i_2}\)
La déviation totale vaut dont: \(D = 2\pi - 2\alpha \) \(D = \frac{{5\pi }}{3}\)
Exercice III
Données: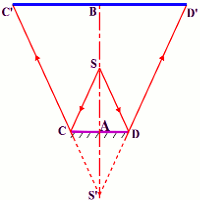
CD=d=8 cm, SA=S’A=20 cm. S’B=20+220= 240 cm, AB=220cm et C’D’=?

CD=d=8 cm, SA=S’A=20 cm. S’B=20+220= 240 cm, AB=220cm et C’D’=?
D’après Thales:
\[\frac{{S'A}}{{S'B}} = \frac{{CD}}{{C'D'}} = \frac{d}{D}\]
\(D = \frac{{S'B}}{{S'A}}d\)
AN : D=96 cm
Exercice IV
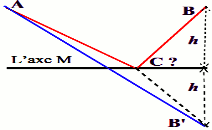
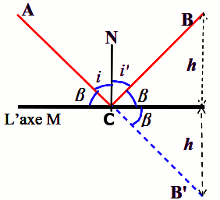
1- Soit B’ le symétrique de B par rapport à l’axe M
La longueur du trajet A-C-B est égale à celle du trajet A-C-B’
Le trajet le plus court est réalisé lorsque C est aligné à A et B’
Cette condition est réalisé si et seulement si i = i’ (voir schéma)
Le trajet solution est A-C-B avec C, le point d’intersection de l’axe M et de la droite (AB’)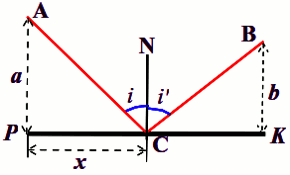

2 La vitesse v du cultivateur Abena étant constante sur tout le trajet, en utilisant le théorème de Pythagore et le fait que \(v = \frac{d}{t}\) , on a:
\({t_1} = \frac{{\sqrt {{a^2} + {x^2}} }}{v}\) Le temps mis par le cultivateur pour parcourir AC
\({t_2} = \frac{{\sqrt {{b^2} + {{\left( {h - x} \right)}^2}} }}{v}\) Le temps mis par le cultivateur pour parcourir CB.
La durée totale sur le parcourt A-C-B sera:
\(t = {t_1} + {t_2}\) \( = f(x)\) \( = \frac{1}{v}\left( {\sqrt {{a^2} + {x^2}} + \sqrt {{b^2} + {{\left( {h - x} \right)}^2}} } \right)\)
Si \(f(x){\rm{ }} = {\rm{ }}\sqrt {u(x)} \), alors \({\rm{ }}f'(x) = \frac{{u'}}{{2\sqrt u }}\)
3 La fonction f (x) admet un minimum si et seulement si \(f'(x){\rm{ }} = {\rm{ }}0\) et \(f''(x){\rm{ }} \succ {\rm{ }}0\)
\(f'(x) = 0\) \( \Rightarrow \frac{x}{{\sqrt {{a^2} + {x^2}} }}\) \( = \frac{{(h - x)}}{{\sqrt {{b^2} + {{\left( {h - x} \right)}^2}} }}\) \({\rm{(1)}}\)
\(f'(0).f'(h) < 0{\rm{ }}\) Cela voudrait dire que la fonction f(x) s’annule au moins un fois dans l’intervalle [o, h]
En élevant (1) au carrée et en évaluant son inverse, on obtient:
En élevant (1) au carrée et en évaluant son inverse, on obtient:
\(\frac{a}{x} = \frac{b}{{(h - x)}}{\rm{ (2)}}\) Cette fonction s’annule dont pour: \({x_0} = \frac{{a.h}}{{a + b}}\)
\(f''({x_0}){\rm{ }} \succ {\rm{ }}0\) la fonction f (x) admet un minimum qui a pour abscisse x0
De la relation (2) et du schéma, nous avons :
De la relation (2) et du schéma, nous avons :
\(\frac{1}{{\tan (i)}} = \frac{a}{x}\) \( = \frac{1}{{\tan (i')}} = \frac{b}{{h - b}}\) soit \(\tan (i) = \tan (i') \Rightarrow i = i'\)
En plaçant une source lumineuse au point A et en remplaçant l’axe M par un miroir. on a l’angle d’incidence égale à l’angle de réflexion i = i’.
« La deuxième lois de Descartes relative à la réflexion est une conséquence du principe de Fermat ».

