Exercice I (série C uniquement) / 5 points
1.a) Montrons en utilisant l’identité de Bézout que a et b sont premiers entre eux
Déterminons deux entiers u et v tels que \(au + \) \(bv = \) \(1\)
On peut écrire
\(5a + \) \(( - 14)b\) \( = \) \(5(14p\) \( + 3) + \) \(( - 14)\) \((5p + 1)\) \( = 70p\) \( + 15\) \( - 70p\) \( - 14\) \( = 1\)
A et b sont donc premiers entre eux 1pt
1.b) Déduisons-en que 87 et 31 sont premiers entre eux
87=14x6+3 et 31=5x6+1
87 et 31 sont ainsi premiers entre eux d’après la question 1.a 0,75pt
1.c) Cherchons tous les couples \(({u_o};{v_o})\) d’entiers tels que \(87{u_o}\) \( + 31{v_o}\) \( = 2\)
Sachant que 5x87+31x(-14)=1, on a 87x10+31(-28)=2x1=2
Prendre \({u_o} = 10\) et \({v_o} = - 28\)
2. Cherchons tous les couples (x ;y) d’entiers tels que (E) \(87x + \) \(31y = 2\)
Soit (x ;y) un couple d’entiers solution de (E), On a \(87x\) \( + 31y\) \( = 2\)
On sait aussi que 87x10+31x(-28)=2x1=2, En multipliant les membres de la deuxième égalité par (-1), puis en additionnant les membres de l’égalité obtenue et de ceux de (E), on obtient 87(x-10)+31(y+28)=0. D’où 87(x-10)=-31(y+28).
87 divise -31(y+28) et est premier avec 31. D’après le théorème de GAUSS, 87 divise y+28 ; y=87k-28 et donc x=-31k+10 où k est entier. On peut vérifier qu’inversement, pour tout entier k, le couple (-31k+10 ; 87k-28) est solution de (E). Les solutions de (E) sont donc tous les couples couple (-31k+10 ; 87k-28) où k est un entier arbitraire. 0,75pts
3. Déterminons les points de (D) vérifiant les conditions du texte
Oit (x ;y) un couple de coordonnées d’un point quelconque de (D). (x ;y) est une solution de (E). Il existe ainsi un entier k tel que \(x = \) \( - 31k + 10\) et \(y = \) \(87k - 28\)
De \(0 \le x\) \( \le 100\), on a \(0 \le \) \( - 31x + 10\) \( \le 100\) et donc \( - \frac{{90}}{{31}} \le \) \(x \le \frac{{10}}{{31}}\)
\(k \in \{ - 1;\) \( - 1;0\} \)
| k | -2 | -1 | 0 |
| x | 72 | 41 | 10 |
| y | 202 | 115 | 28 |
Les points de (D) vérifient les solutions du texte ont pour coordonnées (10 ;28), (41 ;115), (72 ;202) 1,25 pt
Exercice I (Série E uniquement) / 5points
1.a ) Montrons que \(N = \) \(4n - 10\).
Il y a 5-n réponses non correctes ou non données
\(N = 2 \times n\) \( + ( - 2) \times \) \((5 - n) = \) \(4n - 10\) 1 pt
1.b) Déduisons –en l’ensemble des notes possibles qu’un candidat peut avoir à ce test
N peut prendre les valeurs 0 ; 1 ; 2 ; 3 ; 4 ; ou 5 et donc N peut quant à lui prendre les valeurs correspondantes : -10 ; -6 ; -2 ; 2 ; 6 ou 10 1 pt
2.a ) Déterminons les notes possibles de candidat Eya.
On peut avoir les éventualités suivantes pour les trois derniers questions :
- Trois réponses justes exactes ;
- Deux réponses justes exactes ;
- Une réponse juste ;
- Aucune réponse juste
Soit N=10 ou N=6 ou N=2 ou N=-2 1pt
2.b) Calculons les probabilités de A et B
i) \(p(A)\) \( = p(N = 6)\) \( + p(N\) \( = 10)\) \( = \) \(C_3^2{(\frac{1}{3})^2}\) \((\frac{2}{3}) + \) \(C_3^3{(\frac{1}{3})^3}\) \( = \frac{7}{{27}}\) 1pt
ii) \(p(B) = \) \(C_5^4{\left( {\frac{1}{2}} \right)^4}\) \(\left( {\frac{1}{2}} \right) + \) \(C_5^5{\left( {\frac{1}{2}} \right)^5}\) \( = \frac{3}{{16}}\) 1pt
Exercice II / 5 points
1. Calculons les coordonnées de \(\overrightarrow {AM} \wedge \overrightarrow {BM} \)
\(\overrightarrow {AM} \wedge \overrightarrow {BM} \) \( = [(x - 2)\overrightarrow i \) \( + y\overrightarrow j + \) \((z - 1)\overrightarrow k ]\) \( \wedge [(x - 3)\overrightarrow i \) \( + (y + 2)\overrightarrow j \) \( + z\overrightarrow k ]\)
\(\overrightarrow {AM} \wedge \overrightarrow {BM} = \) \([(y - 2z + 2)\overrightarrow i + \) \(( - x - z\) \( + 3)\overrightarrow j + \) \((2x + y\) \( - 4)\overrightarrow k ]\)
Les coordonnées du vecteur \(\overrightarrow {AM} \wedge \overrightarrow {BM} \) sont
\([(y - 2z\) \( + 2);\) \(( - x - \) \(z + 3);\) \((2x + y\) \( - 4)]\) dans la base \((\overrightarrow i ;\overrightarrow j ;\overrightarrow k )\) 1 pt
2. Résolvons le système
\(\left\{ \begin{array}{l} - x + y - 2z = - 4\\ - x - y - z = - 11\\2x + y - z = 8\end{array} \right.\)
Ce système a le même triplet solution que les systèmes
\(\left\{ \begin{array}{l} - x + y - 2z = - 4\\2y - z = 7\\3y - 5z = 0\end{array} \right.\) et
\(\left\{ \begin{array}{l} - x + y - 2z = - 4\\2y - z = 7\\ - 7z = - 21\end{array} \right.\)
Ce qui donne x=3 ; y=5 et z=3 1 pt
3. Montrons qu’il existe un unique point N dont on déterminera les coordonnes et qui vérifie \(\overrightarrow {AN} \wedge \) \(\overrightarrow {BN} = \) \(\overrightarrow {CN} \)
Les coordonnées (x ;y ;z) du possible point N sont solution du système
\(\left\{ \begin{array}{l}y - 2z + 2 = x - 2\\ - x - z + 3 = y - 8\\2x + y - 4 = z + 4\end{array} \right.\) \( \Rightarrow \) \(\left\{ \begin{array}{l} - x + y - 2z = - 4\\ - x - y - z = - 11\\2x + y - z = 8\end{array} \right.\)
qui est exactement le système proposé à la question 2. Or ce système admet pour unique triplet solution, le triplet (3,5,3)
N existe , est unique et a pour coordonnées (3,5,2) dans le repère orthonormé direct \((O;\overrightarrow i ;\overrightarrow j ;\overrightarrow k )\) 1pt
4.a) Montrons que le volume v du tétraèdre ABCN est \(\frac{1}{2}C{N^2}\)
On sait que \(\overrightarrow {AN} \wedge \overrightarrow {BN} \) \( = \overrightarrow {CN} \). Le vecteur \(\overrightarrow {CN} \) est donc orthogonal aux vecteurs \(\overrightarrow {CN} \) et \(\overrightarrow {NB} \)
En considérant le plan (ANB), (CN) est orthogonal au plan (ANB) et par suite, CN est la distance du point C au plan (ANB)
Par conséquent,
\(v = \frac{1}{3} \times \frac{1}{2} \times \) \(\left\| {\overrightarrow {NA} \wedge \overrightarrow {NB} } \right\| \times \) \(CN = \frac{1}{6}C{N^2}\) 1pt
En effet,
\(v = \frac{1}{6} \times \) \(\left\| {\overrightarrow {NA} \wedge \overrightarrow {NB} .\overrightarrow {CN} } \right\|\) \( = \frac{1}{6}\) \(\left| {\overrightarrow {CN} .\overrightarrow {NC} } \right|\) \( = \frac{1}{6}C{N^2}\).
4.b) Calcule de l’aire ABC
\(Aire(ABC)\) \( = \frac{1}{2}\) \(\left\| {\overrightarrow {AB} \wedge \overrightarrow {AC} } \right\|\) \( = \frac{1}{2}\) \(\left| {18\overrightarrow i + 5\overrightarrow j + 8\overrightarrow k } \right|\) \( = \frac{1}{2}\sqrt {413} \) 0,5pt
4.c) Déduisons –en la distance du point N au plan (ABC)
En notant d cette distance, on a
\(v = \frac{1}{3}\) \(Aire(ABC) \times d\) \( \Rightarrow d = \) \(\frac{{3v}}{{Aire(ABC)}}\) \( = \frac{{\sqrt {413} }}{7}\) 0,5pt
Problème /10 points
Partie A :
1.a Résoudre dans \(\mathbb{C}\) l’équation (E) \({z^2} - \) \(3z + 4\) \( = 0\)
Le discriminant de cette équation est \(\Delta = (i\sqrt 7 )\) et ses solutions
\(\frac{{3 - i\sqrt 7 }}{2}\) et \(\frac{{3 + i\sqrt 7 }}{2}\) 0,75pt
1.b Déterminons les module de chaque racine de cette équation
\(\left| {\frac{{3 - i\sqrt 7 }}{2}} \right|\) \( = \) \(\left| {\frac{{3 + i\sqrt 7 }}{2}} \right|\) \( = 2\) 0,5pt
2.a ) Démontrons que z est une racine de E
Comme 0=bar{(A,4) ; (B,-3) ; (C,1)}, on a
\(\frac{{4 \times 1 - 3 \times z + 1 \times {z^2}}}{{4 - 3 + 1}}\) \( = 0\)
Donc \({4 - 3z}\) \({ + {z^2} = 0}\), par conséquent, z est solution de (E) 0,5pt
2.b) Déduisons les coordonnées de B et de C
Puisque z est solution de (E) et \({\mathop{\rm Im}\nolimits} (z) \succ 0\), \(z = \) \(\frac{{3 + i\sqrt 7 }}{2}\), alors \({z^2} = \) \(\frac{{1 + 3i\sqrt 7 }}{2}\)
Donc B a pour coordonnées \(\left( {\frac{3}{2},\frac{{\sqrt 7 }}{2}} \right)\) et C a pour coordonnées \(\left( {\frac{1}{2},\frac{{3\sqrt 7 }}{2}} \right)\) 0,5 pt
3.a) Précisons suivant les valeurs de k l’ensemble \(\left( \Gamma \right)\) des points M du plan tels que \(4M{A^2} - \) \(3M{B^2} + \) \(M{C^2} = k\)
Soit M un point du plan
\(M \in \left( \Gamma \right)\) \( \Leftrightarrow 4M{A^2}\) \( - 3M{B^2}\) \( + M{C^2}\) \( = k\)
\( \Leftrightarrow 2O{M^2}\) \( + 4O{A^2}\) \( - 3O{B^2}\) \( + O{C^2}\) \( = k\)
OA=1, OB=2, OC=4 et \(4O{A^2} - \) \(3O{B^2} + \) \(O{C^2} = 8\)
Donc \(M \in \left( \Gamma \right)\) \( \Leftrightarrow \) \(O{M^2} = \) \(\frac{{k - 8}}{2}\)
• Si \(k \prec 8\) alors \(\left( \Gamma \right) = \phi \)
• Si k=8, alors \(\left( \Gamma \right) = \{ 0\} \)
• Si \(k \succ 8\) alors \(\left( \Gamma \right)\) est le cercle de centre O et de rayon \(\sqrt {\frac{{k - 8}}{2}} \) 1pt
3.b) k=89, Donnons alors une equation catesiene de \(\left( \Gamma \right)\), puis tracons \(\left( \Gamma \right)\) :
Puisque \(89 \succ 8\), \(\left( \Gamma \right)\) est cerce de centre O et de rayon \(\frac{9}{{\sqrt 2 }}\).
Une équation cartésienne de \(\left( \Gamma \right)\) est donc \({x^2} + {y^2}\) \( = \frac{{81}}{2}\) 0,75pt
Partie B
1.a) Dressons le tableau de variation de g :
g est définie sur \(\mathbb{R}\) :
\(\mathop {\lim }\limits_{x \to - \infty } g(x)\) \( = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \) \(g(x) = 1\)
g est derivable sur \(\mathbb{R}\) et pour \(x \in \mathbb{R}\),
\(g'(x)\) \( = 2{e^{ - 2x}}\) \((2x - 2)\)
\(g'(x)\) s’annule en 1, est négative sur \(\left] { - \infty ;1} \right[\) et positive sur \(\left] {1; + \infty } \right[\)
\(g(1) = \) \(1 - {e^{ - 2}}\)
Le tableau de variation est donc le suivant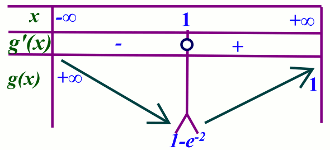 1.b) Déduisons le signe de g(x) suivant les valeurs de x
1.b) Déduisons le signe de g(x) suivant les valeurs de x
\(g(1) = \) \(1 - {e^{ - 2}}\) est le minimum de g sur \(\mathbb{R}\), par suite, pour tout réel x, \(g(x) \ge \) \(g(1) \succ 0\) 0,25pt
2.a) Calculons les limites de f en \( - \infty \) et \( + \infty \) en puis la dérivée de f
\(\mathop {\lim }\limits_{x \to - \infty } \) \(f(x) = - \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \) \(f(x) = + \infty \)
Pour tout réel x, \(f'(x) = \) \(g(x)\) 0,75 pt
2.b) Dressons le tableau de variation de f
Puis que \(f'(x) = \) \(g(x)\) pour tout x, f est strictement croissante sur \(\mathbb{R}\)
Le tableau de variation de f est donc le suivant 0,5pt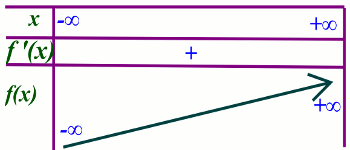 3.a Calcule de \(f(\ln 2)\)
3.a Calcule de \(f(\ln 2)\)
\(f(\ln 2)\) \( = 0\) 0,25pt
3.b ) Déduisons que (D) d’équation
\(y = x\) \( - \frac{5}{4}\ln 2\)
\(\mathop {\lim }\limits_{x \to - \infty } \) \((f(x) - \) \((x - \frac{5}{4}\ln 2)\) \( = \mathop {\lim }\limits_{x \to - \infty } x{e^{ - 2x}}\) \( = - \infty \) 0,25 pt
\(\mathop {\lim }\limits_{x \to + \infty } (f(x)\) \( - (x - \frac{5}{4}\ln 2)\) \( = \mathop {\lim }\limits_{x \to + \infty } x{e^{ - 2x}}\) \( = 0\) 0,25 pt
Donc la droite (D) est une asymptote oblique à la courbe (Cf) en \({ + \infty }\)
• Etude des positions relations de la courbe (Cf) par rapport à la droite (D)
Soit le réel x, \(f(x) - (x\) \( - \frac{5}{4}\ln 2)\)= \(x{e^{ - 2x}}\), l’expression \(x{e^{ - 2x}}\) a le signe de x
Donc la courbe (Cf) coupe la droite (D) au point d’abscisses 0 ; est en dessous de (D) dans le demi-plan (\(x \prec 0\) ) et est au-dessus de (D) dans le demi-plan (\(x \succ 0\)) 0,5 pt
• Traçons la courbe (D) et (Cf) 075 pt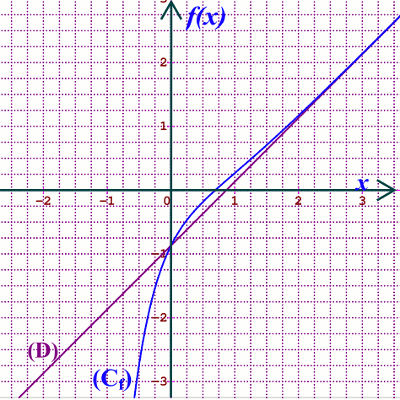 4.a) Déterminons la forme générale des solutions de (E’)
4.a) Déterminons la forme générale des solutions de (E’)
L’équation caractéristique associée à (E’) est : \({r^2} + \) \(4r + 4\) \( = 0\) ; elle a pour solution double -2. La forme générale des solutions de (E’) est :
\(x \mapsto \) \((Ax + B)\) \({e^{ - x}}\) à A et B sont des réels indépendants de x 0,5pt
4.b) Déterminons la solution de (E’) dont la courbe admet une tangente en O parallèle à la droite d’équation \(y = \) \(x + 1\)
Cette solution est de la forme \(x \mapsto \) \((Ax + B)\) \({e^{ - x}}\) ; sa dérivée est :
\(x \mapsto \) \(A{e^{ - 2x}} - \) \(2(Ax + \) \(B){e^{ - x}}\) \( = ( - 2Ax + \) \(A - 2B)\) \({e^{ - 2x}}\)
Comme sa courbe passe par O, on a B=0 et puisque la tangente à sa courbe en O est parallèle à la droite d’équation \(y = \) \(x + 1\), A-2B=1 et ainsi A=1
La solution de (E’) recherchée est donc \(y = \) \(x{e^{ - 2x}}\) 0,5pt
4.c ) Démontrons que f est une solution de l’équation différentielle
\(y'' + \) \(4y' + \) \(4y = \) \(4x - \) \(5\ln 2 + 4\)
Soit un x réel on montre que \(f'' + \) \(4f' + \) \(4f = \) \(4x - \) \(5\ln 2 + 4\) 0,5pt
5.a) En utilisant une intégration par partie, calculons, en cm2, l’aire de (Dλ) en fonction de λ
L’aire (Dλ) est \(( - 2\lambda - \) \(1){e^{ - 2\lambda }}\) \( + 1)c{m^2}\)
5.b) Calculons la limite de cette aire lorsque \(\lambda \to + \infty \)
\(\mathop {\lim }\limits_{\lambda \to + \infty } ( - 2\lambda \) \( - 1){e^{ - 2\lambda }}\) \( + 1) = 1c{m^2}\) 0,5 pt

