A) Évaluation des ressources / 15 points
Exercice 1 : 3 points
On lance deux fois un dé non truqué à six faces portant chacune (de façon distincte), un des nombres \( - \frac{{17}}{3}\) ; -2 ; -1 ; 0 ; 1 ; 2 . On désigne par a le résultat du premier lancé et par b celui du deuxième lancé.
On forme alors la fonction numérique f à variable réelle, définie par :
\(f(x) = \) \(\frac{{a{x^2} + bx + 4}}{{2x - 3}}\)
1. Combien de telles fonctions peut-on former au total ? 1 pt
2. Combien de telles fonctions sont-elles des fonctions homographiques ? 1 pt
3. a) Déterminer l’ensemble de définition de f . 0,25 pt
b) Déterminer le couple (a, b) pour lequel \(f(x) = \) \(x - \frac{4}{3}\) pour \(x \ne \frac{3}{2}\) . 0,75 pt
Exercice 2 : 3,5 points
ABCD est un rectangle de centre 0. I est le milieu de [AB]. Les droites (AC) et (DI) se coupent en E ; les droites (BD) et (IC) se coupent en F.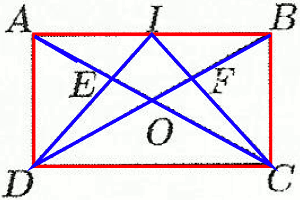 1. Déterminer l'image du triangle ABC par la symétrie orthogonale d’axe (OI). 0,5 pt
1. Déterminer l'image du triangle ABC par la symétrie orthogonale d’axe (OI). 0,5 pt
2. Montrer que le point F est le centre de gravité du triangle ABC. 0,5 pt
3. En déduire que E est le centre de gravité du triangle BAD. 0,5 pt
4. Soit h l’homothétie de centre O qui transforme A en E.
a. Montrer que les droites (EF) et (AB) sont parallèles. 0.5 pt
b. Déterminer h(B). 0.5 pt
5. Soit K = bar{(A, 2); (B, 3); (C, 1)}. Déterminer |’ensemble des points M du plan tels que :
\(||2\overrightarrow {MA} + 3\overrightarrow {MB} + \) \(\overrightarrow {MC} || = ||\overrightarrow {NA} \) \( - \overrightarrow {NB} ||\). 1 pt
Exercice 3 / 4 points
Soit \(\left( {{P_n}} \right)\) la suite définie par \(\left\{ \begin{array}{l}{P_0} = 5000\\{P_{n + 1}} = 1,1{P_n} + 500\end{array} \right.\) pour tout entier naturel n.
1. Soit \(\left( {{Q_n}} \right)\) la suite définie par: \({Q_n} = {P_n} + 5000\).
a) Montrer que \(\left( {{Q_n}} \right)\) est une suite géométrique dont le premier terme et la raison doivent être précisés. 1 pt
b) Exprimer \({Q_n}\) en fonction de n, puis en déduire que \({P_n} = 10000 \times {1,1^n}\) \( - 5000\). 1 pt
2. Une réserve artificielle de poissons avait été inaugurée le 1er janvier 2015 avec 5 000 poissons. Chaque année, ces poissons augmentent (par reproduction) de 10% dans la réserve, et la branche du fleuve qui l’alimente y apporte 500 nouveaux poissons.
Combien de poissons comptera cette réserve le 1er janvier 2030 ? 2 pts
Exercice 4 : 4,5 points
On définit sur \(\left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \) \(\left] {\frac{3}{2}; + \infty } \right[\) la fonction f: par \(f(x) = \) \(\frac{{2{x^2} - 2x + 4}}{{2x - 3}}\), et on désigne par Cf sa courbe dans un repère orthonormé \(\left( {0,\vec i,\vec j} \right)\). Unité sur les axes : 1 cm
1. a) Démontrer que le point \(\Omega \left( {\frac{3}{2};2} \right)\) est un centre de symétrie de Cf. 0,5 pt
b) Déterminer la limite de f à droite en \({\frac{3}{2}}\) et la limite de f en \({ + \infty }\). 0,5 pt
c) Démontrer que la droite \(\Delta :y = \) \(x + \frac{1}{2}\) est asymptote à la courbe de f en \({ + \infty }\); et justifie que la droite \(\Delta ':x = \frac{3}{2}\) est asymptote à la courbe de f . 0,75 pt
2. a) Déterminer l’expression f'(x) de la fonction dérivée f’ de f. 0,5 pt
b) Etudier le signe de f’(x) pour \(x \in \left] {\frac{3}{2}; + \infty } \right[\) . 0,5 pt
c) Dresser le tableau des variations de f sur \(\left] {\frac{3}{2}; + \infty } \right[\) . 0,75 pt
d) Construire la courbe de f sur \(\left] {\frac{3}{2}; + \infty } \right[\) et la compléter pour l’avoir sur \(R - \left\{ {\frac{3}{2}} \right\}\). 1 pt
B) Évaluation des compétences : / 5 points
Situation :
Un parc privé d'aire 750 m2 a la forme d’un triangle rectangle dont le plus grand côté mesure 65 m. Dans ce parc, cohabitent exclusivement des rhinocéros, des taureaux et des oies tous normaux. On y compte 300 pattes, 100 têtes et 65 cornes. Pour sécuriser ce parc, le propriétaire a pour projet de l’entourer avec 3 rangés de fil barbelé qui se vend à 1250 FCFA le mètre sur le marché.
Le vétérinaire veut administrer à chaque oie une dose de vaccin contre la grippe aviaire ; cette dose est celle qui correspond à l'âge médian des oies du parc. La direction de ce parc a reparti par tranche d’âges, les oies dans le tableau ci-dessous.
| Âges en année | [ 0 ; 1 [ | [ 1 ; 2 [ | [ 2 ; 3 [ | [ 3 ; 4 [ | [ 4 ; 5 [ |
| Effectif | 12 | 11 | 4 | 13 | 10 |
Tâches :
1. Déterminer combien il lui faut pour acheter la quantité utile de fil barbelé. 1,5 pt
2. Déterminer le nombre d'animaux de chaque espèce dans ce parc. 1,5 pt
3. Déterminer l’âge qui correspond à la dose de vaccin que recevra chaque oie. 1,5 pt
Présentation : 0,5 pt

