Exercice I / 5 points
1. Dressons le tableau des effectifs de cette série regroupé en classe 1,5 pts

2. Construisons le polygone des effectifs cumulés décroisant 1,5 pt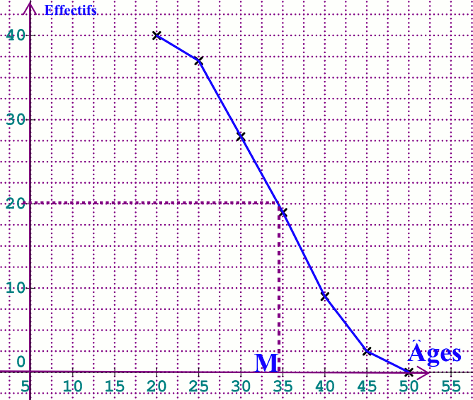
3. Détermination graphique et par calculs de la médiane de cette série statistique 1 pt
• Graphiquement (voir graphe)
• Par calcul, on a, par interpolation linéaire, puisque \(20 \in ]19,29[\), on a
\(\frac{{19 - 29}}{{35 - 30}} = \) \(\frac{{19 - 20}}{{35 - Me}} \Rightarrow \) \(Me = 34,5\) ans
4.a) Détermination du nombre de comités possibles
\(C_{40}^4 = \frac{{40!}}{{36!4!}}\) \( = 91390\) comités 0,5 pts
4.b) Déterminons le nombre de comités comportant 2 femmes 0,5 pt
\(C_5^2C_{35}^2 = 5950\) comités

Exercice II / 4 points
ABC est un triangle tel que AB=4, BC=7 et AC=9
1.a) Montrons que 0,75 pt
\(B{C^2} = \) \(A{B^2} - 2\overrightarrow {AB} .\overrightarrow {AC} \) \( + A{C^2}\)
\(B{C^2} = \) \({(\overrightarrow {BA} + \overrightarrow {AC} )^2} = \) \(B{C^2} = \) \(A{B^2} - 2\overrightarrow {AB} .\overrightarrow {AC} \) \( + A{C^2}\)
1.b) Déduisons-en la valeur de \(\overrightarrow {AB} .\overrightarrow {AC} \) 0,5 pt
\(\overrightarrow {AB} .\overrightarrow {AC} = \) \(\frac{{B{C^2} - A{B^2} - A{C^2}}}{2}\) \( = 24\)
2. Calculons la valeur du \(\cos (\overrightarrow {AB} .\overrightarrow {AC} )\) 0,75 pt
\(\cos (\overrightarrow {AB} .\overrightarrow {AC} ) = \) \(\frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \) \(\frac{{24}}{{36}} = \frac{2}{3}\)
3.a) Calculons la valeur de \(\cos 3\alpha \) 1 pt
\(\cos 3\alpha = \) \(\cos (2\alpha + \alpha )\) \( = 4{\left( {\cos \alpha } \right)^3}\) \( - 3\cos \alpha = \) \( - \frac{{22}}{{27}}\)
3.b) Résolvons dans \(\left[ {0,2\pi } \right[\) l’équation \(\cos 3x = \frac{2}{3}\) 1 pt
\(\cos 3x = \) \(\cos \alpha \Rightarrow \) \(\left\{ \begin{array}{l}3x = \alpha + 2k\pi \\3x = - \alpha + 2k\pi \end{array} \right.\) \( \Rightarrow \) \(\left\{ \begin{array}{l}x = \frac{\alpha }{3} + \frac{{2k\pi }}{3}\\x = - \frac{\alpha }{3} + \frac{{2k\pi }}{3}\end{array} \right.k \in \mathbb{Z}\)
L’ensemble solution dans \(\left[ {0,2\pi } \right[\) est
\(\{ \frac{\alpha }{3};\frac{\alpha }{3} + \frac{{2\pi }}{3};\) \(\frac{\alpha }{3} + \frac{{4\pi }}{3}; - \frac{\alpha }{3} + \frac{{2\pi }}{3};\) \( - \frac{\alpha }{3} + \frac{{4\pi }}{3};\) \( - \frac{\alpha }{3} + 2\pi \} \)

Problème
Partie A
1. Déterminons l’ensemble de définition de f
\(Df = \) \(\mathbb{R} - \left\{ { - 1} \right\}\)
2. Déterminons le signe de f(x) pour \(x \in \left] { - 1; + \infty } \right[\) 0,25 pt
Pour \(x \in \left] { - 1; + \infty } \right[\)\(f(x) \prec 0\)
3. Déterminons une asymptote à \(\left( {{\xi _f}} \right)\) 0,25 pt
\(\left( {{\xi _f}} \right)\) a pour asymptote verticale la droite d’équation x=-1
4. Déterminons une équation de la tengante a \(\left( {{\xi _f}} \right)\) au point d’abscisse -2 0,5 pt
Une équation de la tengante à \(\left( {{\xi _f}} \right)\) au point d’abscisses -2 est : \(y = \) \(f'( - 2)(x + 2) + \) \(f( - 2)\) cette équation sera alors \(y = 2\)
5.a Montrons qua (a, b, c) est solution du système d’équation \(\left\{ \begin{array}{l}y + z = - 2\\x - z = 0\\2x - y + z = - 2\end{array} \right.\)
D’après le tableau de variation de f, f(0)=-2 ; f’(0)=0 et f(-2)=2 avec
\(f(x) = \) \(ax + b + \) \(\frac{c}{{x + 1}}\) et \(f'(x) = \) \(a + \frac{c}{{{{\left( {x + 1} \right)}^2}}}\) on retrouve le système d’équation
5.b Déduisons-en a, b et c 1 pt
\(\left\{ \begin{array}{l}a = - 1\\b = - 1\\c = - 1\end{array} \right.\)
6.a Montrons que la droite d’équation y=-x-1 est asymptote à \(\left( {{\xi _f}} \right)\) en \( - \infty \) et \( + \infty \) 0,5x2=1 pt
\(\mathop {\lim }\limits_{x \to - \infty } f(x)\) \( - ( - x - 1) = \) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{x + 1}} \to 0\) donc y=-x-1 est asymptote à \(\left( {{\xi _f}} \right)\) en \( - \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } f(x)\) \( - ( - x - 1) = \) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{x + 1}} \to 0\) donc y=-x-1 est asymptote à \(\left( {{\xi _f}} \right)\) en \( + \infty \)
6.b Montrons que le point \(\Omega \left( { - 1,0} \right)\) est centre de symétrie de \(\left( {{\xi _f}} \right)\) 1 pt
Il suffit de vérifier que
\(f( - 1 - x)\) \( + f( - 1 + x)\) \( = 0\)
De ce qui précède, nous pouvons conclure que \(\Omega \left( { - 1,0} \right)\) est centre de symétrie à la courbe 1 pt
6.c Construisons \(\left( {{\xi _f}} \right)\) dans le repère orthonormé \((O;\overrightarrow i ;\overrightarrow j )\)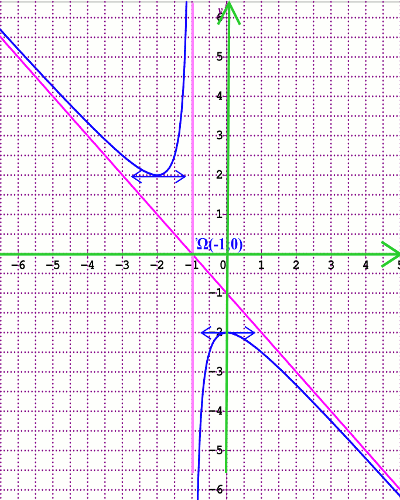
Partie B
1. Plaçons les points A(0;3), B(-2;-5) et C(3 ;0) 0,75 pt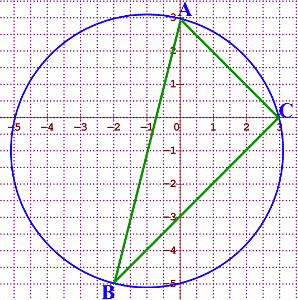
2. Donnons la nature du triangle ABC 0,5 pt
\(AB = \sqrt {68} \), \(AC = \sqrt {18} \) et \(BC = \sqrt {50} \) soit \(A{B^2} = \) \(A{C^2} + B{C^2}\) et d’après la réciproque de la propriété de Pythagore, le triangle ABC est rectangle en C
3. Donnons que une équation cartésienne de \(\left( \Gamma \right)\), le cercle circonscrit au triangle ABC
Soit M(x,y) unpoint de \(\left( \Gamma \right)\), \(M \in \left( \Gamma \right)\) \( \Leftrightarrow 2IM = AB\) où I est le milieu de [AB], ainsi \({(x + 1)^2} + \) \({(y + 1)^2} = 17\)
Donc \(\left( \Gamma \right)\) : \({x^2} + {y^2} + \) \(2x + 2y - \) \(15 = 0\) 0,75 pt

Partie C
1. Montrons que \(\left( {{v_n}} \right)\) est une suite arithmétique de raison \(\frac{1}{2}\)
Soit \(n \in \mathbb{N}\),
\({v_{n + 1}} - {v_n}\) \( = \frac{{{u_n} + 1}}{{2{u_n} - 2}} - \) \(\frac{1}{{{u_n} - 1}} = \frac{1}{2}\)
Déterminons son premier terme
\({v_1} = \frac{1}{{{u_1} - 1}}\) \( = 1\)
Donc \(\left( {{v_n}} \right)\) est une suite arithmétique de raison \(\frac{1}{2}\) et de premier terme \({v_1} = 1\) 1 pt
2. Exprimons \(\left( {{v_n}} \right)\) en fonction de n 1 pt
\({v_n} = \) \({v_1} + \frac{1}{2}(n - 1)\) \( = \frac{1}{2}(n + 1)\)
Exprimons \(\left( {{u_n}} \right)\) en fonction de n
\({v_n} = \) \(\frac{1}{{{u_n} - 1}}\) \( \Rightarrow {u_n} = \) \(\frac{{n + 3}}{{n + 1}}\)
Exprimons \(\left( {{S_n}} \right)\) en fonction de n 0,5 pt
\({S_n} = \) \(\frac{{n(n + 3)}}{4}\)