Partie I : Évaluation des ressources / 24points
Exercice 1 : Vérification des savoirs / 8points
1. Définition :
Lentille mince : c’est un milieu transparent et
homogène délimité par deux surfaces dont l’une au moins est sphérique. 1 pt
Chaleur massique : c’est la quantité de chaleur qu’il faut fournir à un kilogramme d’un corps pour élever sa température d’un degré kelvin. 1 pt
2. Énonçons le théorème de l’énergie cinétique :
« Dans un référentiel galiléen, la variation de l’énergie cinétique d’un solide entre deux instants donnés est égale à la somme algébrique des travaux de toutes mes forces extérieures appliquées au solide pendant cet intervalle de temps ». 2 pts
Il se traduit par la relation : \(\Delta {E_C} = {E_{{C_f}}} - {E_{{C_i}}}\) \( = \sum {W\left( {{F_{ext}}} \right)} \)
Complétons le tableau :
| Défauts d’accommodation | Myopie | Presbytie | Hypermétropie |
| Nature de la lentille | Divergente | Convergente | Convergente |
4. Répondons par Vrai ou Faux : 2 pts
| 4.1 | 4.2 | 4.3 | 4.4 |
| Faux | Faux | Faux | Faux |
5. Un atome émet un photon d’énergie \(\Delta E\) lorsqu’il est dans un état excité (c’est-à-dire dans un état d’énergie supérieure à celle de l’état fondamental). 0,5 pt
Exercice 2 : Application des savoirs /8points
Partie I : Induction magnétique (4pts)
1. Calculons l’intensité du champ magnétique au centre du solénoïde : 1 pt
On a : \(B = {\mu _0}{N_1}I\)
AN : \(B = 6,28 \times {10^{ - 3}}T\)
2.1- Lors de la fermeture et de l’ouverture de l’interrupteur du circuit comprenant le solénoïde S1 , celui-ci subit une variation de l’intensité du courant et par conséquent est le siège d’une auto-induction du fait de la variation de son flux propre. Cette variation du flux propre de S1 entraine aussi la variation du flux du solénoïde S2 , ce qui a pour effet l’apparition d’un courant induit dans S2. 1 pt
2.2- Calculons lors de la fermeture de l’interrupteur la variation du flux à travers S2 : 1 pt
On a : \(\Delta \Phi = {\Phi _f} - {\Phi _i}\) \( = NBS\cos \left( {\widehat {\overrightarrow B ;\overrightarrow S }} \right)\) or \({\Phi _i} = 0\) et \(\left( {\widehat {\overrightarrow B ;\overrightarrow S }} \right) = 0\)
Ainsi : \(\Delta \Phi = NBS\)
AN : \(\Delta \Phi = 9,42 \times {10^{ - 4}}\) Wb
2.3 Déduisons la f.é.m. induite si \(\Delta t = 0,2s\) 1 pt
\(e = - \frac{{\Delta \Phi }}{{\Delta t}}\)
AN : \(e = 4,71 \times {10^{ - 3}}\) v
Partie II : Le microscope (4pts)
1. Calculons l’intervalle optique : 1 pt
On a : \(\overline {{O_1}{O_2}} = \Delta + \) \(\overline {{O_1}F{'_1}} + \overline {{O_2}F{'_2}} \) \( \Rightarrow \Delta = \overline {{O_1}{O_2}} \) \( - \left( {\overline {{O_1}F{'_1}} + \overline {{O_2}F{'_2}} } \right)\)
AN : \(\Delta = 0,2\) m
2. Calculons la puissance intrinsèque : 2 pts
On a : \(P = \) \(\frac{\Delta }{{\overline {{O_1}F{'_1}} \times \overline {{O_2}F{'_2}} }}\)
AN : \(P = 1000\delta \)
3. Calculons le grossissement commercial : 1 pt
On a : \({G_c} = \frac{{Pi}}{4}\) AN : \({G_c} = 250\)
Exercice 3 : Utilisation des savoirs /8points
Partie I : Énergie mécanique [4pts]
1. Faisons le schéma et représentons les forces qui s’appliquent sur S : 1 pt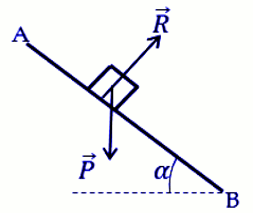 2. Calculons le travail des forces qui s’appliquent sur (S) :
2. Calculons le travail des forces qui s’appliquent sur (S) :
Travail du poids \(\overrightarrow P \) : \({W_{\overrightarrow {AB} }}(\overrightarrow P ) = mgh\) \( = mgAB\sin \alpha \) 1,5 pt
AN : \({W_{\overrightarrow {AB} }}(\overrightarrow P ) = 0,59J\)
Travail de la reaction \(\overrightarrow R \) 0,5 pt
\({W_{\overrightarrow {AB} }}(\overrightarrow R )\) \( = \overrightarrow R .\overrightarrow {AB} = 0\) car \(\overrightarrow R \bot \overrightarrow {AB} \)
3. Calculons la vitesse du solide au point B :
D’après le théorème de conservation de l’énergie mécanique, on a :
\(\Delta {E_c} = - \Delta {E_{pp}}\) \( \Leftrightarrow \frac{1}{2}mv_B^2 = \) \({W_{\overrightarrow {AB} }}(\overrightarrow P )\)
Soit \({v_B} = \) \(\sqrt {\frac{{2{W_{\overrightarrow {AB} }}(\overrightarrow P )}}{m}} \) \( = 4,42\) m/s
Partie II : Lentilles minces (4 pts)
1. Construisons l’image A’B’ de l’objet à travers la lentille : 2 pts
Image lentille divergentes
2. Donnons les caractéristiques de A’B’ : 2 pts
Nature : Réelle et droite
Position : L’image est située sur le plan focal objet de la lentille. On a donc \(\overline {OA'} = 20\) cm
Grandeur : Deux fois plus grande que l’objet, soit \(\overline {A'B'} = 4\) cm
Partie II : Évaluation des compétences / 16 points
Tâche 1 :
En exploitant l’expérience 1 et à partir d’un raisonnement logique, proposons à Maxime la réponse qu’il doit donner à son père pour le thermos :
Il suffit de déterminer la valeur théorique \({\theta _f}\) de la température finale de l’eau, de la comparer à la valeur expérimentale \(\theta \) mesurée puis de conclure.
Données : \(\mu = 200\) g, \({\theta _1} = 20\) oC, \({\theta _2} = 30\) oC m= 500g
A l’équilibre, le principe des échanges thermiques permet d’écrire :
\(\sum {Q = 0} \Leftrightarrow \) \({Q_1} + {Q_2} = 0\)
\(\mu {C_e}\left( {{\theta _f} - {\theta _1}} \right) + \) \(m{C_e}\left( {{\theta _f} - {\theta _2}} \right) = 0\)
Il vient \({\theta _f} = \) \(\frac{{\mu {\theta _1} + m{\theta _2}}}{{\mu + m}}\)
AN : \({\theta _f} = 27,14\) oC
Or la valeur de la température mesurée est \(\theta = 24\) . On Constate que \({\theta _f} \succ \theta \).
Conclusion : Maxime doit dire à son père que le thermos laisse échapper de la chaleur, donc ses clients ont raison de se plaindre.
On peut évaluer la quantité de chaleur perdue par le thermos : on a \(Q = mCe\left( {{\theta _f} - \theta } \right)\) \( = 6584,3J\)
cette quantité de chaleur perdue peut constituer un argument sur la mauvaise qualité du thermos
Tâche 2
En exploitant l’expérience 2 et à partir d’un raisonnement logique, proposons à Maxime la réponse qu’il doit donner à son père pour la pile :
Pour cela il suffit de déterminer le f.é.m expérimentale \({E_{\exp }}\) de la pile dans le montage, de comparer sa valeur à la f.é.m indiquée sur la pile puis de conclure. 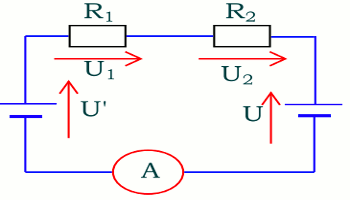 La pile dont on veut déterminer la f.e.m sur comporte en récepteur. D’après la loi de Pouillet on a : \(I = \) \(\frac{{{E_2} - {E_{\exp }}}}{{{r_1} + {r_2} + {R_1} + {R_2}}}\), il vient \(E\exp = {E_2} - \) \(I\left( {{r_1} + {r_2} + {R_1} + {R_2}} \right)\)
La pile dont on veut déterminer la f.e.m sur comporte en récepteur. D’après la loi de Pouillet on a : \(I = \) \(\frac{{{E_2} - {E_{\exp }}}}{{{r_1} + {r_2} + {R_1} + {R_2}}}\), il vient \(E\exp = {E_2} - \) \(I\left( {{r_1} + {r_2} + {R_1} + {R_2}} \right)\)
AN : \(E\exp = 3V\)
Or la valeur indiquée sur la pile est \(E\exp = 3V\). On constate que \({E_1} = 3V\).
Conclusion : Maxime peut rassurer son père de la bonne qualité de la pile et que les clients ont tort de se plaindre.

