Exercice I

1. Le composé étant aromatique, supposons que la molécule de benzène est monosubstituée , on a : \({C_6}{H_5} - {C_x}{H_y}\) soit \({C_8}{H_{10}}\) soit \({C_6}{H_5} - {C_2}{H_5}\)
Par identification, x=2 et y=5
C’est l’éthylbenzène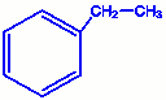Supposons à présent cette molécule disubstituée : \({C_6}{H_4} - {C_x}{H_y}\) qui vaut \({C_8}{H_{10}}\) soit \({C_6}{H_4} - {C_2}{H_6}\) soit \({C_6}{H_4} - {(C{H_3})_2}\)
Par identification, x=2 et y=6
C’est la formule brute du styrène . Elle est de formule semi-développée
C’est le 1,2 dimé-thylbenzène ou l’orthostyrène
C’est le 1,3 diméthylbenzène ou le méta styrène
C’est le 1,4 diméthylbenzène ou le parastyrène
Si la molécule est trisubstituée, nous avons C₆H₃-C₂H₇ ce qui n’est pas possible puisque la tétravalence de l’ un des atomes de carbone dans le substituant C₂H₇ n’est pas respectée.
2. Écrivons les formules semi-développées des hydrocarbures 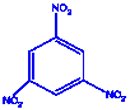a) 1, 3, 5-trinitrobenzène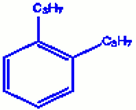b) orthodipropylbenzène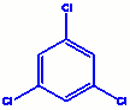c) 1, 3, 5-trichlorobenzène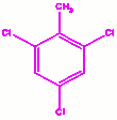d) 2, 4, 6-trichlorotoluène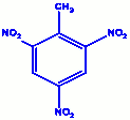e) 2, 4, 6-trinitrotoluènef) Paraxylène
3.1Le chlorure de fer (III), ou chlorure ferrique ou perchlorure de fer est un acide de Lewis, il est utilisé comme catalyseur dans la chloration du benzène.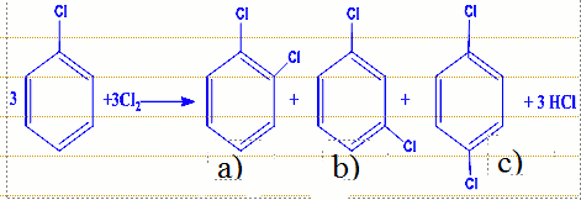a) 1,2-dichlorobenzène ou orthodichlorobenzène
b)1,3-dichlorobenzène ou métadichlorobenzène
c)1,4- dichlorobenzene ou paradichlorobenzène.
3.2. En présence de la lumière utilisé comme catalyseur, la chloruration du benzène produit une fumée blanche : c’est du 1,2,3,4,5,6-hexachlorocyclohexane suivant l’équation :
\({C_6}{H_6} + 3C{{\rm{l}}_2}\)  \(\xrightarrow{lumière}\)  \({C_6}{H_6}C{l_6}\)
4. Un dérivé bromé du benzène contient en masse 50,96 % de brome.
4.1) Déterminons la formule du dérivé en question.
La formule de ce composé est la suivante C₆H_xBr_6-x
\(\% Br = \frac{{(6 - x){M_{Br}}}}{M}.100\), \(\% C = \frac{{72}}{M}.100\),  \(\% H = \frac{x}{M}.100\),
\(\% C + \% H\)  \( = \frac{{72}}{M}.100 + \frac{x}{M}.100\)  \( = 100 - 50,96\)
Le composé est monosubstitué de formule brute C₆H₅Br.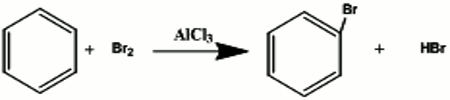5.1 Formule brute du composé
\(\% C = \frac{{12x}}{M}.100\) \( \Rightarrow x = \frac{{\% C \times M}}{{1200}} = 6\)
\(\% C = \frac{y}{M}.100\) \( \Rightarrow y = \frac{{\% H \times M}}{{100}} = 6\)
Ce composé est de formule C₆H₆
5.2.1 Ce composé est le benzène de formule développée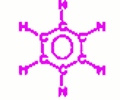5.2.2 Équation de réaction :
\({C_6}{H_6} + 3{H_2}\) \(\xrightarrow{{250^o}C,40 bars, Nickel divisée }\) \({C_6}{H_{12}}\)
C’est une réaction d’addition
5.2.3 Calcule du volume de dihydrogène utilisé. D’après l’équation de réaction :
\(\frac{{{n_{{C_6}{H_6}}}}}{1} = \frac{{{n_{{H_2}}}}}{3}\) \( \Leftrightarrow \) \(\frac{{{m_{{C_6}{H_6}}}}}{{{M_{{C_6}{H_6}}}}} = \frac{{{V_{{H_2}}}}}{{3{V_0}}}\), \({V_{{H_2}}} = \frac{{{m_{{C_6}{H_6}}}}}{{{M_{{C_6}{H_6}}}}} \times 3{V_0}\),  \({V_{{H_2}}} = 16,8L\)
6. Équations de réaction et formules brutes.
a) \({C_6}{H_6} + 3{H_2} \to {C_6}{H_{12}}\)
Le produit est le cyclohexane.
b)  \({C_7}{H_8} + 3{H_2} \to {C_7}{H_{14}}\)
Le produit est le méthylcyclohexane.
c) \({C_6}{H_6} + C{l_2} \to \) \({C_6}{H_5}Cl + HCl\)
Le produit est le monochlorobenzène et l’ acide chloridrique (HCl).
d)  \({C_6}{H_5}Cl + C{l_2}\)  \( \to {C_6}{H_4}C{l_2} + HCl\)
Le produit est le dichlorobenzène et l’acide chloridrique (HCl).

Exercice II

A. Nombre de mole de monochlorobenzène obtenu
De l’expression du rendement, nous avons :
\(r = \frac{{{n_{b(reagi)}}}}{{{n_{b(initial)}}}}100\) \( = \frac{{{m_{b(reagit}}}}{{{M_b}}} \times \frac{{{M_b}}}{{{m_{_{b(initial)}}}}}100\) \( = \frac{{{m_{b(reagit}}}}{{{m_{_{b(initial)}}}}}100\)
\({m_{b(reagi)}} = \frac{r}{{100}}{m_{_{b(initial)}}}\) soit \({m_{b(reagit)}} = 2,4g\)
De l’équation de réaction :
\({C_6}{H_6} + C{l_2}\) \(\xrightarrow{AlCl3}\) \({C_6}{H_5}Cl + HCl\)
\({n_{{C_6}{H_6}}} = {n_{{C_6}{H_6}Cl}}\) \( = \frac{{{m_{b(reagi)}}}}{{{M_{{C_6}{H_6}}}}} = \frac{{2,4}}{{78}}\) \( = 0,031mol\)
B. Le mélange de dihydrogène et de 0,50 g de benzène passe sur du nickel chauffé à 200°C conduit au cyclohexane suivant l’équation :
\({C_6}{H_6} + 3{H_2}\) \(\xrightarrow{{250^o}C,40 bars, Ni }\) \({C_6}{H_{12}}\)
Calcule de la masse du cyclohexane de l’équation de réaction
\(\frac{{{m_B}}}{{{M_B}}} = \frac{{{m_{cyclohexane}}}}{{{M_{cyclohexane}}}}\)  \( \Rightarrow {m_{cyclohexane}}\) \( = \frac{{{m_B}}}{{{M_B}}}{M_{cyclohexane}}\)
\({m_{cyclohexane}} = 0,577g\)
La combustion du cyclohexane est donnée par l’équation :
\({C_6}{H_{12}} + 9{O_2}\) \( \to 6C{O_2} + 6{H_2}O\)
Calcule de la masse de cyclohexane ayant réagi :
\(\frac{{{m_{{H_2}O}}}}{{6{M_{{H_2}O}}}} = \frac{{m{'_{cyclohexane}}}}{{{M_{cyclohexane}}}}\),  \(m{'_{cyclohexane}} = \frac{{{m_{H2O}}}}{{6{M_{H2O}}}}{M_{cyclohexane}}\), \(m{'_{cyclohexane}} = 0,45g\)
Calcule du rendement : \(r = \frac{{n{'_{cyclohezane}}}}{{{n_{cyclohezane}}}} \times 100\) \( = \frac{{m{'_{cyclohezane}}}}{{{m_{cyclohezane}}}} \times \frac{{{M_{_{cyclohezane}}}}}{{{M_{cyclohezane}}_{}}}100\) \( = \frac{{m{'_{cyclohezane}}}}{{{m_{cyclohezane}}}}100\) \( = \frac{{0,45}}{{0,577}}100 = 80\% \)

Exercice III

1. Déterminons la formule brute de B. Relation entre la masse de carbone et celle d’hydrogène \(\left. \begin{array}{c}{m_C} \to {m_H}\\6 \to 1\end{array} \right\} \Rightarrow {m_C} = 6{m_H}\)
Ainsi : \(\% C = \frac{{{m_C}}}{{{m_B}}}100\),  \(\% C = \frac{{6{m_H}}}{{{m_B}}}100{\rm{ }}\),  \(\% H = \frac{{{m_H}}}{{{m_B}}}100\)
\(\frac{{\% C}}{{\% H}} = 6 \Rightarrow \% C = 6\% H\),  \(\% H = \frac{{100}}{7} = 14,30\), \(\% C = 100 - 14,30 = 85,70\)
Supposons cet hydrocarbure de formule C_xH_y, ainsi : \(\% C = \frac{{1200x}}{{{M_B}}} \Rightarrow x = 8\),  \(\% H = \frac{{100y}}{{{M_B}}} \Rightarrow y = 16\)
2. Le composé B est de formule C₈H₁₆.
B est obtenu par hydrogénation
\({C_8}{H_{10}} + 3{H_2} \to {C_8}{H_{16}}\)
NB : Le composé B, bien étant saturé ne respecte pas la formule générale de alcane C_nH_2n+2, il est de formule C_nH_2n, c’est un alcane cyclique.
3. Formules développées possibles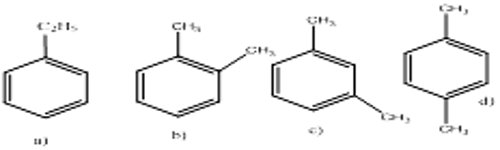4. a) Équation de réaction
\({C_8}{H_{10}} + xC{l_2}\) \( \to {C_8}{H_{10 - x}}C{l_x}\) \( + xHCl\)
\(\% Cl = \frac{{35,5x}}{{{M_C}}}100{\rm{ ; }}\)  \({\rm{ }}\% C + \% H = \frac{{106 + x}}{{{M_C}}}100\)
Après combinaison des deux équations vous obtenez x=1,  C vaut C₈H₉Cl
4.b) L’équation de réaction devient
\({C_8}{H_{10}} + C{l_2}\) \( \to {C_8}{H_9}Cl + HCl\)
5.a Conditions expérimentales : l’alkylation du benzène est catalysé par un acide de Lewis (AlCl₃, FeCl₃ ..) et en absence de lumière.
Équation de réaction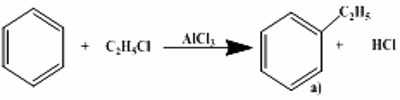5.b) Le produit obtenu a) est l’éthylbenzène.

Exercice IV

1. Formules brutes des hydrocarbures de formule générale C₇Hy 
\(\frac{M}{{100}} = \frac{y}{{\% H}}\) \( \Rightarrow y = \frac{{84}}{{\frac{{100}}{{\% H}} - 1}}\)
Pour 8,69%, y=8 et la formule brute de la molécule est : C₇H₈.
Pour 14,28%, y=14 et la formule brute de la molécule est : C₇H₁₄.
Pour 16%, y=16 et la formule brute de la molécule est : C₇H₁₆.
Les seules formules brutes liées par une hydrogénation catalytique sont données par cette équation
\({C_7}{H_8} + 3{H_2}\)  \(\xrightarrow{{250^o}C,40 bars, Ni }\) \({C_7}{H_{14}}\)
Le composé C₇H₁₄ obéit à l’équation générale C_nH_2n, c’est est un alcane cyclique ou un alcène. Si c’est un alcène, il peut donner une réaction d’ addition, alors, c’est un alcane cyclique
2.a Le composé C vaut (C₇H₁₆ ) et est un alcane:
2.b De l’équation précédente, B vaut ( C₇H₈ ), C’est le méthylbenzène
Le composé A vaut (C₇H₁₄) est un alcane cyclique, C’est méthylcyclhexane
\(B + C{H_3}Br\) \(\xrightarrow{FeBr3 }\) \(D + HBr\)
C’est le 1,2 dimé-thylbenzène ou l’orthostyrène
C’est le 1,3 diméthylbenzène ou le méta styrène
C’est le 1,4 diméthylbenzène ou le parastyrène
3.b) D’après la représentation spatiale du parastyrène, sa monochloration ne donnera qu’un seul isomère, le composé D est le parastyrène.
Équation de réaction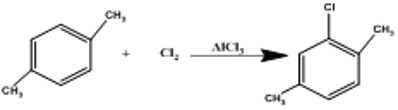

Exercice V

5.a) Équation de réaction
\({C_7}{H_8} + HN{O_3}\) \(\xrightarrow{H2SO4}\) \({C_7}{H_7}N{O_2} + {H_2}O\)
Formule développée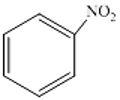La réaction à lieu en présence de H₂SO₄.   
5.b) Calcule de la quantité de matière du nitrotoluène
\({C_7}{H_8}\left\{ \begin{array}{l}{m_1} = 100 \times {10^3}g\\{M_1} = 92g/mol\end{array} \right.\)   r = 90%
Le C₇H₈ et C₇H₇NO₂ réagissent mole à mole, soit : \({m_2} = \frac{{100 \times {{10}^3}}}{{92}}137\)  \( = 149 \times {10^3}g\)
m₂ est ici la masse théorique du nitrotoluène, la masse réelle m’₂ est obtenue en tenant compte du rendement de la réaction. \(m{'_2} = \frac{{90}}{{100}}.149 \times {10^3}\) \( = 134 \times {10^3}g\)
5.c) Calcule du volume de para nitrotoluène
Soit m_m la masse de métatoluène
m_O la masse de l’orthotoluène
m_P la masse de paratoluène restante
\({m_m} = \frac{2}{{100}}m{'_2}\) \( = \frac{2}{{100}}134 \times {10^3}\) \( = 2682g\)
\({m_O} = \frac{{0,5}}{{100}}m{'_2}\) \( = \frac{{0,5}}{{100}}134 \times {10^3} = 670g\)
\({m_P} = \) \(m{'_2} - {m_m} - {m_O}\) \( = 130648g\)
Calcule du volume du paranitrotoluène obtenu.
\(\rho  = \frac{{{m_P}}}{{{V_P}}} \Rightarrow \) \({V_P} = \frac{{{m_P}}}{\rho } = \frac{{130648}}{{1100}}\) \( = 118,78l\)