Situation problème
Votre camarade de classe vous rapporte une question qui a été posé par son neveu, à savoir pourquoi le son d’une voiture est plus aigu quand celle-ci se rapproche de lui et plus grave quand elle s’éloigne de lui ?
Aide ton camarade à trouver une solution pour son neveu.

L’effet Doppler est le décalage de fréquence d’une onde sonore entre la mesure à l’émission et sa mesure à la réception lorsque la distance entre l’émetteur et le récepteur varie au cours du temps.
Il a été découvert par Christian Doppler au XIXème Il est utilisé encore aujourd’hui dans de nombreux domaines de la vie courante et de la recherche.
Le nom d'« effet Doppler-Fizeau » est réservé aux ondes électromagnétiques.

Globalement, l’effet Doppler est la variation de la fréquence (longueur d’onde) d’une onde mécanique ou électromagnétique en fonction de la vitesse relative de la source et du récepteur.

I. Généralités sur les phénomènes périodiques

La fréquence d’un signal périodique dépend du référentiel dans lequel il est observé, lorsque la source et le récepteur sont en mouvement relatif, le signal émis par la source et celui reçu par le récepteur n’ont pas la même fréquence.
\(\Delta f = {f_R} - {f_S}\).
On distinguera dans ce cas deux types de période :
• La période propre T, qui est la période de cette onde dans le référentiel lié à la source.
• La période apparente \(Ta\), qui est la période de cette onde dans le référentiel lié au récepteur.
Ceci est justifié par le fait que la distance entre l’émetteur et le récepteur varie au cours d’une période de l’onde émisse, donc le temps de trajet entre la première émission et sa réception et la deuxième émission et sa réception sont différents. Ainsi :
• Si la source et le récepteur sont immobiles \(Ta = T\) ;
• Si la source se rapproche du récepteur immobile (ou si le récepteur se rapproche de la source immobile) alors \(Ta \prec T\) ;
• Si la source s’éloigne du récepteur immobile (ou si le récepteur s’éloigne de la source immobile) \(Ta \succ T\)
• Récepteur et source en mouvement, plusieurs configurations peuvent se présenter, nous les analyserons en détails dans la suite de ce cours.

II. Manifestations de l’effet Doppler

Parlant de l’effet Doppler, on distinguera l’émetteur de l’onde et son récepteur. Le récepteur perçoit une onde sonore ayant les mêmes caractéristiques (fréquence, période et longueur d’onde) lorsque l’émetteur et le récepteur sont immobiles, on ne constate donc pas d’effet Doppler.

II.1 Emetteur se rapprochant du récepteur immobile

N.B. Pour tous les calculs, on supposera que le mouvement relatif entre l’émetteur et le récepteur se fasse selon la droite les joignant.

Soit S, la source de l’onde, qui émet un signal de fréquence \(f\) et de période \(T\), \(v\) la vitesse de l’onde et \({v_s}\) la vitesse de la source.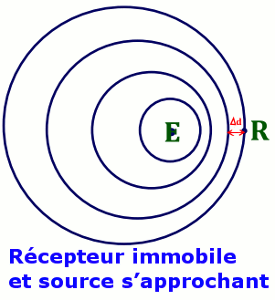
Le premier front d’onde va parcourir une distance \(d = vT\) lorsque la source aura parcouru quant à elle une distance \({d_s} = {v_s}T\) avant d’émettre le deuxième front d’onde.
La distance séparant les deux fronts d’onde consécutifs est alors :
\(\Delta d = d - {d_s}\) \( = T\left( {v - {v_s}} \right)\)
La période apparente sera dont \(Ta = \frac{{\Delta d}}{v} = \) \(\frac{{d - {d_s}}}{v} = \) \(T\frac{{\left( {v - {v_s}} \right)}}{v}\) et la fréquence apparente \({f_a} = \frac{1}{{Ta}} = f\frac{v}{{\left( {v - {v_s}} \right)}}\)

II.2 Émetteur s’éloignant du récepteur immobile

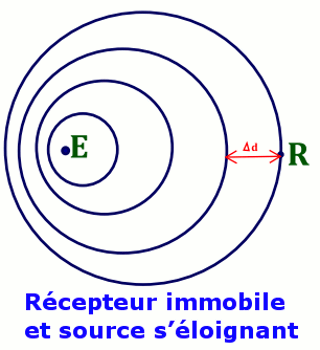Dans ce cas, \(\Delta d = d + {d_s}\) \( = T\left( {v + {v_s}} \right)\)
La fréquence apparente est donc
\({f_a} = \frac{1}{{Ta}} = f\frac{v}{{\left( {v + {v_s}} \right)}}\)

II.3 Récepteur en mouvement, émetteur fixe

Soit S, la source de l’onde, qui émet un signal de fréquence \(f\) et de période \(T\), \(v\) la vitesse de l’onde et \({v_r}\) la vitesse du récepteur.
Pour simplifier notre raisonnement, nous alors supposer que la distance entre l’émetteur et le récepteur est \(d\) qui est encore la distance parcourue par l’onde pendant une période (longueur d’onde) et l’origine des temps et des espaces étant centrée sur l’émetteur, ainsi :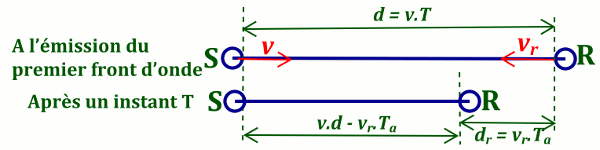
• La distance parcourue par le premier front d’onde est : \(d = vT\) ;
• La distance parcourue par le récepteur est : \({d_r} = {v_r}Ta\).
• La distance parcourue par le deuxième front d’onde est : \({d_2} = v.T - {v_r}Ta\) qui vaut encore \(v.Ta\);
\(v.T - {v_r}.Ta = \) \(v.Ta \Rightarrow Ta = \) \(T\frac{v}{{v + {v_r}}}\)
La fréquence apparente s’écrit donc : \({f_a} = f\frac{{v + {v_r}}}{v}\)

II.4 Récepteur et source en mouvement

Si l’émetteur et le récepteur se déplacent sur une même droite. Trois possibilités se présenteront.
• Le repère d’étude est un point du milieu dans lequel se propage l’onde (par exemple l’atmosphère pour une onde sonore) ;
• Le repère d’étude est lié à l’émetteur (source) ;
• Le repère d’étude est lié au récepteur.
Nous allons faire notre étude en supposant le repère d’étude lié à l’émetteur (source).
Par convention, les vitesses seront comptées comme positives suivant la direction et dans le sens de propagation du signal (de l’émetteur vers le récepteur). Ainsi une vitesse \({{v_s}}\) positive et \({{v_r}}\) négative correspondra à un rapprochement entre source et récepteur tandis qu’une vitesse \({{v_s}}\) négative et \({{v_r}}\) positive correspondra à un éloignement.

a) Source et récepteur se déplaçant dans le même sens

Avant le croisement : \({f_a} = f\left( {\frac{{v + {v_r}}}{{v - {v_s}}}} \right)\)
Après le croisement : \({f_a} = f\left( {\frac{{v - {v_r}}}{{v + {v_s}}}} \right)\)

b) Source et récepteur se déplaçant dans le sens inverse

Avant le dépassement : \({f_a} = f\left( {\frac{{v - {v_r}}}{{v - {v_s}}}} \right)\)
Après le dépassement : \({f_a} = f\left( {\frac{{v - {v_r}}}{{v + {v_s}}}} \right)\)

RQ : Toutes les vitesses qui ne sont pas dans la direction de l’onde émise par la source sont comptées négativement, \({{v_s}}\) ( source immobile) et \({{v_r}}\) ( récepteur immobile) peuvent être nulle, on retrouve ainsi les expressions précédentes.

III. Les applications de l’effet Doppler

L’effet Doppler est principalement utilisé pour déterminer une vitesse, quel que soit le domaine d’application mais peut également servir à déterminer la distance entre deux objets (GPS, échographie) ou la présence d’une exo-planète en astronomie.
L’effet Doppler s’utilise dans les radars, le GPS, en médecine (échographie) et l’astrophysique.

Conclusion

L’effet Doppler est un phénomène observé lorsque la source et le récepteur sont en mouvement relatif l’un par rapport à l’autre. En effet, il se produit alors un décalage en fréquence qui s’exprime de manière différente suivant le mouvement de la source et du récepteur.