Situation problème
Kenfack dispose d’une bobine idéale d’inductance L sur laquelle aucune information n’est mentionnée, il souhaite connaitre la valeur de L, pour cela il fait un montage constitué de cette bobine et d’un condensateur de capacité C =100μF.
Des enregistrements lui ont permis d'obtenir à chaque instant la tension aux bornes de la bobine $u(t) = 100$ $\cos \left( {2 \times {{10}^{ - 4}}t} \right)$.
Aide cet élève à retrouver la valeur de l’inductance L.

I. Etude théorique du circuit LC

Réunissions les deux armatures A est B d’un condensateur chargé aux bornes N et M d’une bobine purement inductive.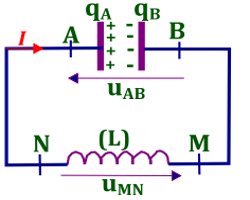
Choisissions un sens algébrique pour l’intensité $i$, d’après la loi des mailles, à chaque instant, nous aurions : ${u_{AB}} + {u_{MN}} = 0$
${u_{AB}} = \frac{q}{C}$, ${u_{MN}} = L\frac{{di}}{{dt}}$ $= L\frac{{{d^2}q}}{{d{t^2}}}$ car $i = \frac{{dq}}{{dt}}$
il vient alors que $\frac{{{d^2}q}}{{d{t^2}}} + \frac{q}{{LC}} = 0$
Qui est une équation différentielle donc la solution est de la forme :
$q(t) =$ ${Q_m}\cos \left( {\omega t + \varphi } \right)$
Avec ${Q_m}$ la charge maximale, $\varphi$ la phase à l’instant initial des constantes qui sont déterminées à l’aide des conditions initiales.
$\ddot q(t) =$ ${Q_m}{\omega ^2}\cos \left( {\omega t + \varphi } \right)$ $= {\omega ^2}q(t)$ en le remplaçant dans l’équation différentielle précédente, nous avons : $LC{\omega ^2} = 1$
Soit $\omega = \frac{1}{{\sqrt {LC} }}$ est la pulsation propre de l’oscillateur, le circuit est donc le siège d’oscillations électriques libres non amorties de période propre.
$T = \frac{{2\pi }}{\omega }$ $= 2\pi \sqrt {LC}$ encore appelée Formule de Thomson.

NB : $\omega$ est généralement noté ${\omega _0}$ et est la pulsation propre de l’oscillateur
En effet, Il y a charges et décharges successives du condensateur, on dit que le système oscille.
L’armature A chargée initialement par exemple positivement se charge négativement tandis que l’armature B prend une charge positive et ainsi de suite.
Il y’a un changement périodique du signe des charges portées par les armatures du condensateur.
${\omega _0}$, ${T_0}$, ${N_0}$ sont appelés respectivement pulsation propre, période propre et fréquence propre du circuit oscillant.
L’intensité du courant est donnée par la relation
$i(t) = \frac{{dq}}{{dt}} =$ $- {\omega _0}{Q_m}\sin ({\omega _0}t + \varphi )$ $= {I_m}\cos ({\omega _0}t +$ $\varphi + \frac{\pi }{2})$
Avec ${I_m} = {\omega _0}{Q_m}$ l’intensité maximale du courant ou amplitude de l’intensité.
L’intensité est aussi une fonction sinusoïdale du temps; Elle est en quadrature avance (déphasage de $\frac{\pi }{2}$) avec la charge du condensateur.

II. L’énergie électromagnétique :

L’énergie électromagnétique $E$ d’un circuit oscillant LC est la somme de l’énergie magnétique de la bobine et de l’énergie électrique du condensateur
$E = {E_{mag}} + {E_{ele}}$ $= \frac{1}{2}L{i^2} + \frac{1}{2}\frac{{{q^2}}}{C}$
L’énergie de cet système étant conservatif, nous avons
$\frac{{dE}}{{dt}} = \frac{d}{{dt}}$ $\left( {\frac{1}{2}L{i^2} + \frac{1}{2}\frac{{{q^2}}}{C}} \right) = 0$
$Li\frac{{di}}{{dt}} + \frac{q}{C}\frac{{dq}}{{dt}} =$ $L\frac{{di}}{{dt}} + \frac{q}{C} = 0$
avec $i = \frac{{dq}}{{dt}}$, on retrouve l’équation différentielle précédente régissant les oscillations du système
$\frac{{{d^2}q}}{{d{t^2}}} + \frac{q}{{LC}} = 0$

On montre également que l’énergie du système se conserve en remplaçant dans l’expression de l’énergie totale $q(t) =$ ${Q_m}\cos ({\omega _0}t + \varphi )$ et $i(t) = - {\omega _0}{Q_m}$ $\sin ({\omega _0}t + \varphi )$
$\omega _0^2 = \frac{1}{{LC}} \Rightarrow$ $L\omega _0^2 = \frac{1}{C}$
$E = \frac{1}{2}L\omega _0^2Q_m^2$ ${\sin ^2}({\omega _0}t + \varphi ) + \frac{1}{{2C}}Q_m^2$ ${\cos ^2}({\omega _0}t + \varphi )$
$E = \frac{1}{2}L\omega _0^2Q_m^2$ $({\sin ^2}({\omega _0}t + \varphi ) +$ ${\cos ^2}({\omega _0}t + \varphi ))$
$E = \frac{1}{2}L\omega _0^2Q_m^2$ $= \frac{1}{{2C}}Q_m^2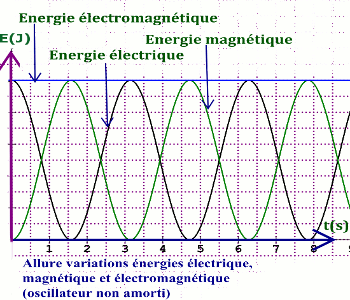$L’énergie électromagnétique du circuit LC se conserve.