Cours relativement hermétique : bien vouloir faire beaucoup d’exercices

Objectif
Déterminer un arbre couvrant d’un graphe et déterminer un arbre couvrant de poids minimum d’un graphe pondéré.

Motivation
Rechercher un réseau de coût minimum dans l’établissement d’un réseau de communication ou d’interconnexion.

Prérequis : Notion de théories des graphes.

Situation problème : Quel est le nombre minimum de couleurs nécessaires pour colorier les pays d’une carte géographique de manière telle que des couleurs distinctes soient attribuées à des pays voisins?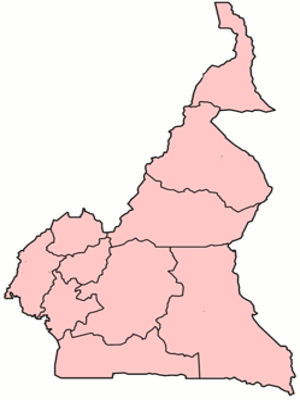
NB : On considère un graphe ayant pour sommet les différents régions de la carte. Deux sommets sont adjacents si et seulement si ils partagent une frontière.

L'ordre d'un graphe |V| est son nombre de sommets.
La taille d'un graphe est |E|, son nombre d'arêtes.
Le degré ou la valence d'un sommet est le nombre d'arêtes incidentes à ce sommet, où une boucle compte double.
NB : Vertex (v) (sommet) et edges (e) (arêtes ) d’où les notations (v,e)

I. Graphes Connexes

Un graphe H est appelé sous-graphe d’un graphe G, si H est identique à G ou si H est obtenu de G par suppression de sommets et / ou arêtes.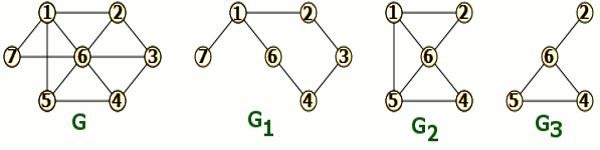
Une chaîne dans un graphe G , est une suite \(({v_1},{e_1},...,\) \({v_{q - 1}},{e_q},{v_q})\) ayant pour éléments alternativement des sommets et des arêtes, commençant et se terminant par un sommet, et telle que chaque arête est encadrée par ses extrémités.
Une chaine est simple si les arêtes \(({e_1},...,{e_q})\) sont deux à deux distinctes.
Une chaine est fermée lorsque \({v_1} = {v_q}\)
Soit le graphe suivant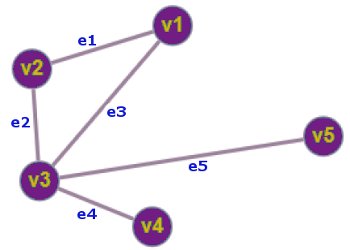
Autrement dit :
Une chaîne élémentaire est une chaîne ne passant pas deux fois par un même sommet, c'est-à-dire dont tous les sommets sont distincts.
\(({v_1},{e_1},{v_2},\) \({e_2},{v_3},{e_5},{v_5})\)
Une chaîne simple est une chaîne ne passant pas deux fois par une même arête, c'est-à-dire dont toutes les arêtes sont distinctes.
\(({v_1},{e_1},{v_2},\) \({e_2},{v_3},{e_5},{v_5})\)
Un cycle est une chaîne simple dont les deux extrémités sont identiques.
\(({v_1},{e_1},{v_2},{e_2},\) \({v_3},{e_3},{v_1})\)
Un chemin est une chaine dans laquelle aucun sommet ni arête n’est répété.
Un graphe est dit connexe si pour toute paire u et v de sommets, il existe un chemin dans le graphe contenant u et v.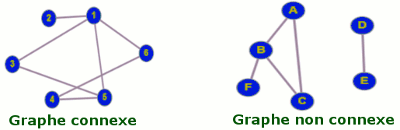
Un arbre est un graphe connexe ne contenant aucun cycle.
Un arbre couvrant d’un graphe connexe G est un arbre qui est un sous-graphe de G et qui contient chaque sommet de G.
L’arbre couvrant est dit pondéré si chaque arête est affectée d’un poids.

Le théorème suivant donne la relation qui existe entre la notion de connexité et celle d’arbre couvrant.

Théorème
Un graphe est connexe si et seulement si il contient un arbre couvrant.

Certains algorithmes permettent de construire un arbre couvrant d’un graphe et un arbre couvrant de poids minimum. Nous pouvons citer :
• Algorithme de parcours en largeur (BFS : Breadth-First Search en anglais)
• Algorithme de Prim
• Algorithme de Kruskal

II. Algorithmes de construction d’un arbre couvrant d’un graphe et un arbre couvrant de poids minimum

II.1 Algorithme de parcours en largeur (BFS : Breadth-First Search)

L'algorithme de parcours en largeur permet de calculer les distances de tous les nœuds depuis un nœud source dans un graphe non pondéré (orienté ou non orienté). Il peut aussi servir à déterminer si un graphe non orienté est connexe.
Il permet de construire un arbre couvrant d’un graphe ou d’établir qu’il n’en existe pas un. En fonction du résultat de cet algorithme, le théorème précédent permet de conclure sur la connexité du graphe.

Principe de l’algorithme de parcours en largeur

1. Choisissez un sommet de départ, S , et étiquetez-le 0.
2. Trouvez tous les sommets adjacents à S et étiquetez-les 1.
3. Pour chaque sommet marqué d’un 1, trouvez une arête qui le relie au sommet étiqueté 0, assombrir ces arêtes.
4. Recherchez les sommets non étiquetés adjacents à ceux avec l’étiquette 1 et étiquetez-les 2. Pour chaque sommet étiqueté 2, trouvez une arête qui le relie à un sommet étiqueté 1. Assombrissez cette arête. S’il existe plus d’une arête, choisissez-en une arbitrairement.
5. Continuez ce processus jusqu’à ce qu’il n’y ait plus de sommets sans étiquette adjacents à ceux étiquetés. Si tous les sommets du graphe ne sont pas étiquetés, alors il n’existe pas d’arbre couvrant pour le graphe. Si tous les sommets sont étiquetés, alors les sommets et les arêtes assombries forment un arbre couvrant du graphe.

II.2 Algorithme de Prim

Il permet de déterminer un arbre couvrant de poids minimum. Cet algorithme trouve un sous-ensemble d'arêtes formant un arbre sur l'ensemble des sommets du graphe initial et tel que la somme des poids de ces arêtes soit minimale.

Principe de l’algorithme de Prim

1. Trouvez l’arête avec les plus petits poids dans le graphe. L’assombrir et encerclez ses deux sommets. Les liens sont rompus arbitrairement.
2. Trouvez l’arête avec le plus petit poids parmi les arêtes non assombris restants ayant un sommet encerclé et un sommet non encerclé. Assombrir cette arête et son sommet non encerclé.
3. Répétez l’étape 2 jusqu’à ce que tous les sommets soient encerclés.

II.3 Algorithme de Kruskal

l'algorithme de Kruskal est un algorithme de recherche d'arbre recouvrant de poids minimum (ARPM) ou arbre couvrant minimum (ACM) dans un graphe connexe non-orienté et pondéré. Il a été conçu en 1956 par Joseph Kruskal.
Cette algorithme permet également de déterminant un arbre couvrant de poids minimum dans un graphe connexe non orienté et pondéré. Contrairement à l’algorithme de Prim, l’algorithme de Kruskal nécessite auparavant le tri des arêtes. Cette condition permet de simplifier grandement le fonctionnement de l’algorithme.

Principe l’algorithme de Kruskal

1. Triez les Arêtes en ordre croissant.
2. Répétez : Ajoutez l’arête de poids minimum parmi les arêtes disponibles
• Si l’arête ajoutée forme un cycle, recommencez avec la prochaine arête.
• S’il ne reste plus d’arêtes, l’arbre couvrant de poids minimum est déterminé avec succès.
• Si tous les sommets sont atteints par des arêtes et que tous les sommets sont dans un seul ensemble disjoint, l’algorithme s’arrête, car l’arbre couvrant de poids minimum est déterminé.

III. Graphes et sous graphes pondérés, plus court chemin

Un graphe valué

C’est un graphe pour lequel chaque arête est associée à un nombre réel appelé poids. Si ce nombre est positif, on parle alors de graphe pondéré.

Le poids d’un sous graphe (resp. d’un chemin) dans un graphe valué

C’est la somme des poids des arêtes composant ce sous graphe (resp. ce chemin).

III.1 Algorithme de Dijkstra

Il permet de déterminer un chemin de poids minimum entre deux sommets d’un graphe.

III.1 Principe

1. Sélectionner le sommet de départ \(u\) et fixer son poids à 0.
2. Attribuer provisoirement un poids \(\infty \) aux autres sommets.
3. Tant qu’il reste des sommets dont les poids ne sont pas définitivement fixés, répéter les instructions suivantes :
• Parmi les sommets dont le poids n’est pas définitivement fixé, choisir un sommet X dont le poids p est minimal, puis fixer définitivement p comme poids.
• Pour tous les sommets Y dont le poids n’est pas définitivement fixé et qui sont adjacents au dernier sommet fixé X, calculer la somme s du poids de X et du poids de l’arête reliant X à Y.
• Si la somme s est inférieure au poids provisoirement affecté au sommet Y, affecter provisoirement à Y le nouveau poids s et indiquer en indice le sommet X pour se souvenir de sa provenance.
• Si la somme s est supérieure au poids provisoirement affecté au sommet Y, on ne change rien.
4. Quand le sommet d’arrivé v est définitivement fixé : Le chemin de poids minimum se lit à l’envers, de \(v\) à chacun de ses prédécesseurs successifs.

IV. Graphes eulériens et graphes hamiltoniens

Les notions de graphes eulériens et de graphes hamiltoniens, qui sont particulièrement utiles dans la résolution d’un grand nombre de problèmes concrets tels que : Les sept ponts de Königsberg, ), le problème du voyageur de commerce (Travel Salesman Problem), le coloriage…

On appelle cycle eulérien d’un graphe G un cycle contenant une et une seule fois toutes les arêtes de G.
Un graphe est dit eulérien s’il possède un cycle eulérien.
On appelle chaîne eulérienne d’un graphe G une chaîne passant une et une seule fois par chacune des arêtes de G.
Un graphe ne possédant que des chaînes eulériennes est semi-eulérien.

NB : Un graphe est eulérien (ou semi-eulérien) s’il est possible de dessiner le graphe sans lever le crayon et sans passer deux fois sur la même arête.

Théorème
Un graphe connexe possède un cycle eulérien si et seulement si tous ses sommets sont de degré pair.

Un chemin hamiltonien est un chemin qui visite chaque sommet d’un graphe exactement une fois.
Un cycle hamiltonien est un chemin hamiltonien qui commence et se termine au même sommet.
Un graphe est dit hamiltonien s’il possède un cycle hamiltonien.
Un graphe ne possédant que des chaînes hamiltoniennes est semi-hamiltonien.

Remarque : La condition nécessaire et suffisante pour visiter tous les sommets d’un graphe sans lever le crayon est que le graphe soit hamiltonien.

Propriété (Conditions Nécessaires)
• Un graphe possédant un sommet de degré 1 ne peut pas être hamiltonien.
• Si un sommet dans un graphe est de degré 2, alors les deux arêtes incidentes à ce sommet doivent faire partie du cycle hamiltonien.
• Les graphes complets sont hamiltoniens.

Théorème (Condition Suffisante)
Soit G un graphe simple d’ordre \(n \ge 3\). Si pour toute paire \(\{ x,y\} \) de sommets non adjacents, on a \(d(x) + d(y)\) \( \ge n\) alors G est hamiltonien.

Corollaire : Soit G un graphe simple d’ordre \(n \ge 3\). Si pour tout sommet x de G, on a \(d(x) \ge \frac{n}{2}\) alors G est hamiltonien.

Théorème (Formule d’Euler)
Dans un multi-graphe planaire connexe (fini) possédant \(s\) sommets, \(a\) arêtes et \(f\) faces, on a \(s - a + f = 2\)