Correction exercice I
1. Démontrons que la fonction \(x \mapsto \) \(\tan \left( {\frac{{{x^2} - 1}}{{{x^2} + 1}}} \right)\) est continue en \( \mathbb{R}\)
La fonction \(f(x) = \) \(\frac{{{x^2} - 1}}{{{x^2} + 1}}\) est continue sur \( \mathbb{R}\) et on a : \(f(\) \( \mathbb{R}\) \() \subset \left] { - 1;1} \right[\).
La fonction \(g:y \mapsto \tan y\) est continue sur \(\left] { - \frac{\pi }{2};\frac{\pi }{2}} \right[\) et on a \(\left] { - 1;1} \right[ \subset \) \(\left] { - \frac{\pi }{2};\frac{\pi }{2}} \right[\)
Donc, la fonction \(g \circ f:x \mapsto \) \(\tan \left( {\frac{{{x^2} - 1}}{{{x^2} + 1}}} \right)\) est continue sur \( \mathbb{R}\)
2. Etudions la continuité de la fonction \(f(x)\) au point \({x_0}\) donné dans chacun des cas suivant:
a) \(\left\{ \begin{array}{l}f(x) = \frac{{{x^2} - 4}}{{x - 2}}\\f(x) = 4\end{array} \right.\) avec \({x_0} = 2\)
\(f(x)\) est continue en \({x_0} = 2\), si \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}}\) \( = f(2)\)
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}}\) \( = \frac{0}{0}\) indétermination
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}} = \) \(\mathop {\lim }\limits_{x \to 2} \frac{{\left( {x + 2} \right)\left( {x - 2} \right)}}{{x - 2}}\) \( = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4\)
Alors f est continue en \({x_0} = 2\)
b) \(\left\{ {\begin{array}{*{20}{l}}{f(x) = \frac{{\left| {x - 1} \right| + 2}}{{x + 3}}}\\{f(1) = \frac{1}{2}}\end{array}} \right.\) avec \({x_0} = 1\).
Ecrivons \(f(x)\) sans le symbole de la valeur absolue :
Si \(x \in \left] { - \infty ;1} \right]\) alors \(f(x) = \frac{{ - x + 3}}{{x + 3}}\)
Si \(x \in \left] {1, + \infty } \right]\), alors \(f(x) = \frac{{x + 1}}{{x + 3}}\)
Ainsi étudions la continuité de \(f\) à gauche et à droite de \({x_0} = 1\)
\(f\) est continue en \({x_0} = 1\) si \(f(1)\) existe et si \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \) \(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \) \(f(1) = \frac{1}{2}\) ce qui est vraie, donc \(f(x)\) est continue en \({x_0} = 1\)
3. Dans chacun des cas suivants, préciser l’ensemble de définition de la fonction \(f\) puis dire si elle est prolongeable par continuité au point \({x_0}\).
a) \(\left\{ \begin{array}{l}f(x) = \frac{{x - \sqrt x }}{x}\\{x_0} = 0\end{array} \right.\) ;
\(Df = \left] {0; + \infty } \right[\)
\(f\) n’est pas définie en \({x_0} = 0\) donc elle n’est pas continue en \({x_0} = 0\)
\({\mathop {\lim }\limits_{x \to 0} \frac{{x - \sqrt x }}{x} = }\) \({\mathop {\lim }\limits_{x \to \infty } \frac{{x - 1}}{{x + \sqrt x }} \to \infty }\)
Alors \(f\)n’est pas continue en\({x_0} = 0\).
Par conséquent \(f\) n’est pas prolongeable par continuité en \({x_0} = 0\).
b) \(\left\{ \begin{array}{l}f(x) = \frac{{\tan x}}{x}\\{x_0} = 0\end{array} \right.\).
\(Df = \) \( \mathbb{R}\) \( - \left\{ {\frac{{k\pi }}{2}} \right\}\) avec \(k \in \) \( \mathbb{R}\)
Etudions la continuité de \(f\) en \({x_0} = 0\).
\(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x}}{x} = 1\)
Par conséquent \(f\) est prolongeable par continuité en \({x_0} = 0\) et son prolongement par continuité en \({x_0} = 0\) est la fonction \(h\) définie par :
\(h(x) = \) \(\left\{ \begin{array}{l}\frac{{\tan x}}{x}{\rm{ si }}x \ne 0\\1{\rm{ si }}x = 0\end{array} \right.\)
Correction exercice II
1. On considère la fonction \(g(x)\) définie sur \(\left[ { - 2;3} \right]\) par \(g(x) = 2x – 4\).
Démontrons qu’il existe \(\alpha \in \left[ { - 2;3} \right]\) tel que \(f(\alpha ) = - 4\)
\(g(x)\) est continue en \(\left[ { - 2;3} \right]\), et \(f\left( {\left[ { - 2;3} \right]} \right)\) \( = \left[ { - 8;2} \right]\).
De plus \( - 4 \in \left[ { - 8;2} \right]\), donc d’après le théorème des valeurs intermédiaires, il existe \(\alpha \in \left[ { - 2;3} \right]\) tel que \(f(\alpha ) = - 4\).
2.1 Calculons la limite en 1 de la fonction
\(\forall x \in \) \( \mathbb{R}\) \( - \left\{ 1 \right\}\), \(f(x) = \) \(\frac{{3\left( {x + 1} \right)}}{{\sqrt {3{x^2} + 1} + 2}}\) donc
\(\mathop {\lim }\limits_{x \to 1} f(x) = \) \(\mathop {\lim }\limits_{x \to 1} \frac{{3\left( {x + 1} \right)}}{{\sqrt {3{x^2} + 1} + 2}}\) \( = \frac{3}{2}\)
2.2 \(\forall x \in \) \( \mathbb{R}\), \(g(x) = \) \(\left\{ \begin{array}{l}f(x)\\g(1) = \frac{3}{2}\end{array} \right.\)
3.1 La fonction \(g(x) = 1 - {x^2}\) est continue sur \(\left[ { - 1;1} \right]\) et \(g\left( {\left[ { - 1;1} \right]} \right) = \) \(\left[ {0,1} \right]\)
La fonction \(h(x) = \sqrt x \) est continue sur \(\left[ {0; + \infty } \right[\) et \(\left[ {0;1} \right] \subset \) \(\left[ {0; + \infty } \right[\)
Donc, la fonction \(f = h \circ g\) est continue sur \({\left[ { - 1;1} \right]}\)
3.2 La fonction \(g(x) = \sin x\) est continue sur \( \mathbb{R}\) et \(g(\) \( \mathbb{R}\) \() = \left[ { - 1;1} \right]\)
La fonction \(h(x) = \) \(\frac{{x + 1}}{{{x^2} + 1}}\) est continue sur \( \mathbb{R}\) et \(\left[ { - 1,1} \right] \in \) \( \mathbb{R}\)
Donc, la fonction \(f = h \circ g\) est continue sur \( \mathbb{R}\)
Correction exercice III
Soit \(f\) la fonction définie sur \(\left[ {1; + \infty } \right[\) par \(f(x) = \) \(\sqrt {x - 1} - 2\)
1. Etudions la continuité de \(f\) sur l’intervalle \(\left[ {1; + \infty } \right[\).
La fonction \(g:x \mapsto x - 1\) est continue sur \(\left[ {1; + \infty } \right[\) et \(g\left( {\left[ {1; + \infty } \right[} \right) = \) \(\left[ {0; + \infty } \right[\)
La fonction \(h:x \mapsto \sqrt x \) est continue sur \(\left[ {0; + \infty } \right[\)
La fonction \(p:x \mapsto x - 2\) est continue sur \( \mathbb{R}\) et \(\left[ {0; + \infty } \right[ \subset \) \( \mathbb{R}\)
Donc, la fonction \(f = p \circ h \circ g\) est continue sur \({\left[ {1; + \infty } \right[}\)
2. Justifions que \(\forall x \in \left[ {1; + \infty } \right[\), \(f(x) \ge - 2\).
En effet, \(\forall x \in \left[ {1; + \infty } \right[\), \(f(x) + 2 \ge 0\); donc \(\forall x \in \left[ {1; + \infty } \right[\) \(f(x) \ge - 2\)
3. Démontrons que tout élément \(\beta \) de \(\left[ { - 2; + \infty } \right[\) a un antécédent \(\alpha \) dans \(\left[ {1; + \infty } \right[\)
On vient de démontrer que \(f\left( {\left[ {1; + \infty } \right[} \right)\) \( \subset \left[ { - 2; + \infty } \right[\)
Réciproquement, pour tout \(\beta \) de \(\left[ { - 2; + \infty } \right[\), il existe \(\alpha = 1 + {\left( {2 + \beta } \right)^2}\) tel que \(\beta = f(\alpha )\)
En déduire l’image par \(f\) de l’intervalle \(\left[ {1; + \infty } \right[\).
Donc \(\left[ { - 2; + \infty } \right[ \subset \) \(f\left( {\left[ {1; + \infty } \right[} \right)\) par suite \(f\left( {\left[ {1; + \infty } \right[} \right)\) \( = \left[ { - 2; + \infty } \right[\)
Correction exercice IV
1. Dans chacun des cas suivants, déterminons \(\alpha \) pour que la fonction \(f\) soit continue sur \( \mathbb{R}\)
a) \(f(x) = \) \(\left\{ \begin{array}{l}{f_1}(x) = \frac{{{x^2} - x}}{x}\\{f_2}(0) = \alpha \end{array} \right.\), avec \({f_1}(x)\) si \(x \in \) \( \mathbb{R^*}\) ;
En raisonnant comme précédemment, vous trouverez
\(\alpha = - 1\).
b) \(f(x) = \) \(\left\{ \begin{array}{l}{f_1}(x) = \frac{{\sqrt {{x^2} - x} + 1 - x}}{x}\\{f_2}(1) = \alpha \end{array} \right.\), avec \({f_1}(x)\) si \(x \in \) \( \mathbb{R}\) \(\backslash \left\{ 1 \right\}\)
En raisonnant comme précédemment, vous trouverez
\(\alpha = - \frac{1}{2}\)
2. Les fonctions suivantes sont-elles prolongeables par continuité en 0 ?
a) \(f(x) = \) \({x^2}\sin \frac{1}{x}\) ;
\(\forall x \in \) \( \mathbb{R^*}\); \( - {x^2} \le f(x)\) \( \le {x^2}\), donc \(\mathop {\lim }\limits_{x \to 0} f(x) = 0\)
Soit \(F\) le prolongement par continuité de \(f\) en 0, on a : \(\forall x \in \) \( \mathbb{R^*}\); \(F(x) = f(x)\) et \(F(0) = 0\)
b) \(g(x) = \) \(\frac{{{{\sin }^2}x}}{x}\).
On a : \(\forall x \in \) \( \mathbb{R^*}\); \(g(x) = \) \(x{\left( {\frac{{\sin x}}{x}} \right)^2}\); donc \(\mathop {\lim }\limits_{x \to 0} g(x) = 0\)
Soit \(G\) le prolongement par continuité de \(g\) en 0, on a : \(\forall x \in \) \( \mathbb{R^*}\);
\(G(x) = g(x)\) et \(G(0) = 0\)
Correction exercice V
A.1 Démontrons que l’équation \({x^3} - 6x\) \( - 6 = 0\) a une unique solution réelle.
La fonction \(f(x) = {x^3} - 6x\) \( - 6 = 0\) est dérivable sur \( \mathbb{R}\) et a pour dérivée
\(f'(x) = 3{x^2}\) \( - 6 = 3\) \(\left( {x + \sqrt 2 } \right)\) \(\left( {x - \sqrt 2 } \right)\)
On en déduit le tableau de variation suivant 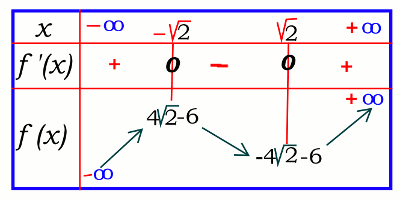 \(f\) est continue et strictement monotone sur chacun des intervalles \(\left] { - \infty ; - \sqrt 2 } \right]\), \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\) et \(\left[ {\sqrt 2 ; + \infty } \right[\) et de plus \(0 \in f\left( {\left[ {\sqrt 2 ; + \infty } \right[} \right)\) donc l’equation \(f(x)=0\) admet une solution unique \(\alpha \) dans \({\left[ {\sqrt 2 ; + \infty } \right[}\)
\(f\) est continue et strictement monotone sur chacun des intervalles \(\left] { - \infty ; - \sqrt 2 } \right]\), \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\) et \(\left[ {\sqrt 2 ; + \infty } \right[\) et de plus \(0 \in f\left( {\left[ {\sqrt 2 ; + \infty } \right[} \right)\) donc l’equation \(f(x)=0\) admet une solution unique \(\alpha \) dans \({\left[ {\sqrt 2 ; + \infty } \right[}\)
A.2 Déterminons une valeur approchée à \({10^{ - 2}}\) près de cette solution.
\(\alpha = 2,85\)
B.1 Démontrons que l’équation \(\frac{1}{4}{x^3} - {x^2}\) \( + 1 = 0\) a trois solutions réelles
La fonction \(f(x) = \frac{1}{4}{x^3}\) \( - {x^2} + 1\) est dérivable sur \( \mathbb{R}\) et sa dérivé est \(f'(x) = \) \(\frac{3}{4}x\left( {x - \frac{8}{3}} \right)\)
Soit le tableau de variation suivant :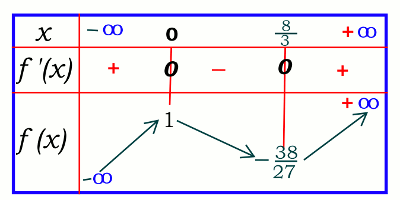 \(f\) est continue et strictement monotone sur chacun des intervalles \(\left] { - \infty ;0} \right]\), \(\left[ {0;\frac{8}{3}} \right]\) et \({\left[ {\frac{8}{3}; + \infty } \right[}\)
\(f\) est continue et strictement monotone sur chacun des intervalles \(\left] { - \infty ;0} \right]\), \(\left[ {0;\frac{8}{3}} \right]\) et \({\left[ {\frac{8}{3}; + \infty } \right[}\)
De plus 0 appartient à chacun des intervalles \(\left] { - \infty ;1} \right]\), \(\left] {1; - \frac{{38}}{{27}}} \right[\) et \(\left] { - \frac{{38}}{{27}}; + \infty } \right[\)
Donc l’équation \(f(x)=0\) admet trois solutions \(\alpha \), \(\beta \) et \(\gamma \) telles que \(\alpha \in \left] { - \infty ;1} \right]\), \(\beta \in \left] {1; - \frac{{38}}{{27}}} \right[\) et \(\gamma \in \left] { - \frac{{38}}{{27}}; + \infty } \right[\)
B.2 Déterminons une valeur approchée à \({10^{ - 2}}\) près de ces solutions.
\(\alpha = - 0,90\), \(\beta = 1,19\) et \(\gamma = 3,71\)
Correction exercice VI
1. On a : \(f(x) = 0 \Leftrightarrow \) \(\cos x - x = 0\), \(f\) est continue sur \(\left[ {0;\frac{\pi }{3}} \right]\), \(f(0) = 1\) et \(f(\frac{\pi }{3}) = \) \(\frac{1}{2} - \frac{\pi }{3} \prec 0\), ainsi \(f(0) \times f(\frac{\pi }{3}) \prec 0\). Onc l’equation \(f(x) = 0 \) admet une solution \({x_0}\) dans \(\left] {0;\frac{\pi }{3}} \right[\).
2. D’après ce qui précède, on a : \(0 \prec {x_0} \prec \frac{\pi }{3}\)
\(\frac{{0 + \frac{\pi }{3}}}{2} = \frac{\pi }{6}\), \(f(\frac{\pi }{6}) = \) \(\frac{{\sqrt 3 }}{2} - \frac{\pi }{6}\) \( \succ 0\) et \(f(\frac{\pi }{3}) = \prec 0\), \(f(\frac{\pi }{6}) \times f(\frac{\pi }{3}) \prec 0\) soit \(\frac{\pi }{6} \prec {x_0} \prec \frac{\pi }{3}\).
\(\frac{{\frac{\pi }{6} + \frac{\pi }{3}}}{2} = \frac{\pi }{4}\), et \(f(\frac{\pi }{4}) \times f(\frac{\pi }{6}) \prec 0\) soit \(\frac{\pi }{6} \prec {x_0} \prec \frac{\pi }{4}\)
\(\frac{{\frac{\pi }{6} + \frac{\pi }{4}}}{2} = \frac{{5\pi }}{{24}}\) et \(f(\frac{\pi }{4}) \times f(\frac{{5\pi }}{{24}}) \prec 0\) soit \(\frac{{5\pi }}{{24}} \prec {x_0} \prec \frac{\pi }{4}\)
\(0,65 \prec \frac{{5\pi }}{{24}} \prec {x_0}\) \( \prec \frac{\pi }{4} \prec 0,79\)
Ainsi, 0, 7 est la valeur approchée de \({x_0}\) à 0,1 près.