L’épreuve comporte trois exercices et un problème sur deux pages.
Exercice l (3,5 points)
1. a) Exprimer \(\cos 2\alpha \) en fonction de \(\cos \alpha \), puis en fonction de \(\sin \alpha \). 0,5 pt
b) Sachant que \(\frac{\pi }{4} = 2\frac{\pi }{8}\), en déduire les valeurs exactes de \(\cos \frac{\pi }{8}\) et \(\sin \frac{\pi }{8}\). 0,5 pt
e) En déduire les valeurs exactes de \(\cos \frac{{5\pi }}{8}\) et \(\sin \frac{{5\pi }}{8}\). 0,5 pt
d) Déterminer la valeur exacte du réel \(A = \cos \frac{{9\pi }}{8}\) \( + \cos \frac{{7\pi }}{8}\) \( + 2\sin \frac{{5\pi }}{8}\) 0,5 pt
2. ABCDEFGH est un octogone régulier de centre O, OA = 1.
On se propose de calculer son aire. Soit I le milieu de [AB]. On pose \(\alpha=mes\widehat{AOI} \).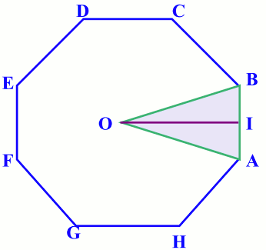
a) Exprimer OI et AI en fonction de \(\alpha \). 0,5 pt
b) En déduire que \(aire(OAB) = \) \(\frac{1}{2}\sin 2\alpha \). 0,25 pt
c) Déterminer l’aire de l’octogone ABCDEFGH. 0,25 pt
3. Soit r un réel strictement positif.
Déterminer, en fonction de r, Faire d‘un octogone régulier inscrit dans un cercle de rayon r. 0,5 pt

Exercice 2 (3 points)
l. Soient: A et B deux points du plan tels que AB = 5. On désigne par l le milieu de [AB].
a) Déterminer l’ensemble (C) des points M du titan tels que \(M{A^2} + \) \(M{B^2} = 25\). 0,5 pt
b) Déterminer l’ensemble (D) des points M du plan tels que \(M{A^2} - \) \(M{B^2} = 0\) 0,25 pt
2. Le plan est rapporte’ au repère orthonormé \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\). Unité graphique 1 cm.
On donne les points A(- 3, 1) et B(2, 1).
a) Déterminer une équation du cercle \(\left( \Gamma \right)\) de diamètre [AB] et tracer \(\left( \Gamma \right)\). 0,5 pt
b) Vérifier que le point D( - 2, 3) appartient à \(\left( \Gamma \right)\) et déterminer une équation de la tangente (T) à \(\left( \Gamma \right)\) en D. 0,75 pt
e) Vérifier que le point E(2, 6) est extérieur à \(\left( \Gamma \right)\). Tracer le cercle \(\left( {\Gamma '} \right)\) de diamètre [EI], où I désigne le milieu de [AB]. En déduire les coordonnées des points de contact des tangentes a \(\left( {\Gamma '} \right)\) menées de E. 1 pt

Exercice 3 (2,5 points)
P et Q sont deux points du plan tels que PQ = 1. On note (C) le cercle de centre P et de rayon 3, (C’) le cercle de centre Q et de rayon 2. La demi-droite [PQ) coupe de cercle (C) au point l.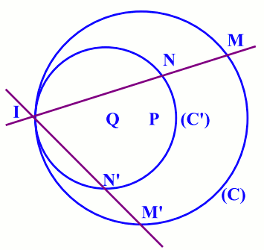
l. Justifier que le point l appartient aussi à (C’). 0,5 pt
2. Déterminer le centre et le rapport de l’homothétie qui transforme (C) en (C’). 1 pt
3. Soient M et M’ deux points de (C). Les droites (IM) et: (IM’) coupent (C’) en N et N’ respectivement.
a) Montrer que les droites (MM’) et (NN’) sont. parallèles. 0,5 pt
b) Déterminer la valeur du rapport \(\frac{{NN'}}{{MM'}}\). 0,5 pt

Problème (11 points)
Le plan est rapporté au repère orthonormé \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\).
Partie A/
Dans cette partie, on n’essayera pas de réduire l’expression de \(f(x)\) au même dénominateur, mais on utilisera les propriétés sur la somme de deux fonctions.
Soit \(f\) la fonction definie sur \(Df = \) \(\Re - \left\{ { - 1,1} \right\}\) par \(f(x) = \) \(\frac{1}{2}\left( {\frac{1}{{x + 1}} + \frac{1}{{x - 1}}} \right)\). On note \(\left( {{C_f}} \right)\) sa courbe représentative.
l. Étudier la parité de la fonction \(f\). Que peut-on en déduire pour la courbe \(\left( {{C_f}} \right)\)? 0,5 pt
2. Calculer les limites de \(f\) en \( - \infty \), à gauche et à droite en -1 et 1, et en \( + \infty \). Fn déduire les asymptotes à la courbe \(\left( {{C_f}} \right)\). 2 pts
3. Déterminer l’expression de la dérivée \(f'\) de la fonction \(f\). En déduire le sens de variation de la fonction \(f\). 1 pt
4. a) Donner une équation de la tangente (T) à \(\left( {{C_f}} \right)\) au point d'abscisse 0. 0,25 pt
b) Étudier le signe de \(f(x) + x\) sur \(Df\) et donner la position de (T) par rapport à \(\left( {{C_f}} \right)\). 0,75 pt
5. a) Tracer (T) et \(\left( {{C_f}} \right)\). 1 pt
b) Tracer sur le même graphique la courbe (Cg) représentative de la fonction g définie sur \(Df\) par \(g(x) = \left| {f(x)} \right|\) 0,75 pt
c) Discuter graphiquement, suivant les valeurs de m, le nombre et le signe des solutions de l’équation \(g(x) = m\). 0,75 pt

Partie B/
On considère la suite \(\left( {{u_n}} \right)\) à termes positifs donnée par :
\({u_0} = 2\) et pour tout entier naturel \(n\), \({u_n} = \frac{{2{u_{n - 1}}}}{{{u_n}}}\)
l. a) Exprimer \({u_{n + 1}} - 1\) en fonction de \({u_{n - 1}}\) et comparer leur signe. 0,5 pt
b) Quel est le signe de \({u_0} - 1\). Que peut-on en déduire ? 0,5 pt
2. a) Exprimer \({u_{n - 1}} - {u_n}\) en fonction de un. 0,5 pt
b) En déduire le sens de variation de la suite (un). 0,5 pt
3. On pose \({v_n} = \frac{1}{{{u_n} - 1}}\)
a) Montrer que \(\left( {{v_n}} \right)\) est une suite arithmétique de raison 1. 0,5 pt
b) Exprimer \({{v_n}}\) en fonction de \(n\). 0,5 pt‘
c) En déduire l’expression de \({u_n}\) en fonction de \(n\) 0,5 pt
d) Calculer la limite de la suite \(\left( {{u_n}} \right)\). 0,5 pt