Baccalauréat
Physique
C & E
2012
Enoncés
Bonjour ! Groupe telegram de camerecole, soumettrez-y toutes vos préoccupations. forum telegram
Exercice 1: Mouvements dans les champs de forces et leurs applications
A– Mouvement dans le champ de pesanteur
Prendre g = 10 m.s2 et négliger la résistance de l’air.
Deux joueur de football Sorel et Jean II, de tailles respectives h1 = 1,80m et h2 = 1,60 m, s’entrainent au jeu de tête avec un ballon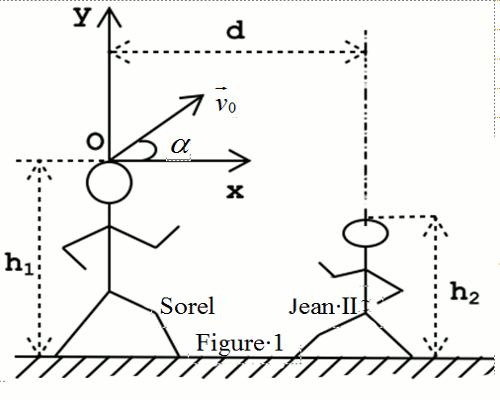
que l’on supposera ponctuel. Après un coup de tête, le ballon part de Sorel vers Jean II avec une vitesse initiale \({\overrightarrow v _o}\) faisant un angle α = 45° avec l’horizontale. On prendra v0 = 10 m/s. La figure 1 ci-contre présente la situation.
que l’on supposera ponctuel. Après un coup de tête, le ballon part de Sorel vers Jean II avec une vitesse initiale \({\overrightarrow v _o}\) faisant un angle α = 45° avec l’horizontale. On prendra v0 = 10 m/s. La figure 1 ci-contre présente la situation. A.1. En prenant pour origine des espaces, le sommet de la tête de Sorel et pour instant initial l’instant de départ du ballon, établir l’équation cartésienne de la trajectoire du centre d’inertie G du ballon.
A.2. L’équation de la trajectoire de G peut se mettre sous la forme \(10y + {x^2} - 10 = 0\).
A quelle distance d de Sorel, doit se placer Jean II pour que le ballon retombe exactement sur sa tête?
B– Mouvement d’une particule chargée dans un champ magnétique uniforme
Une particule de masse m=6,64 10-27 kg et de charge q=+3,2 10-19 C entre avec une vitesse de valeur v = 1,5 105 m.s-1 dans une région de largeur l = 18 cm où règne un champ magnétique uniforme \(\overrightarrow B \) d’intensité B = 3 10-3 T orthogonal à la vitesse de la particule.
B.1. En négligeant son poids, déterminer la nature du mouvement de la particule dans la zone où règne le champ magnétique.
B.2. Etablir l’expression du rayon de courbure R de sa trajectoire puis calculer sa valeur.
B.3. Calculer la valeur de l’angle de déviation α de la trajectoire de la particule sous l’influence du champ magnétique.
Exercice 2 : Systèmes oscillants
A– Oscillateur mécanique
Dans la gorge d’une poulie (P) de rayon r = 10 cm et dont on veut déterminer le moment d’inertie JΔ , on fait passer une ficelle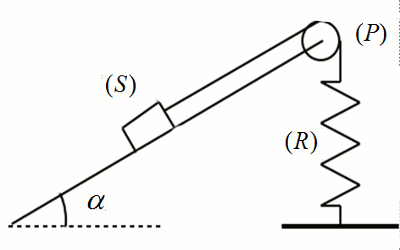
inextensible de masse négligeable. A l’une des extrémités de cette ficelle, on accroche un solide (S) de mase m = 100 g et reposant sur un plan incliné d’angle α = 30° sur l’horizontale. L’autre extrémité de la ficelle est reliée à un ressort ( R ) de raideur k = 10 N.m-1 et de masse négligeable. On prendra g = 10 m.s-2
inextensible de masse négligeable. A l’une des extrémités de cette ficelle, on accroche un solide (S) de mase m = 100 g et reposant sur un plan incliné d’angle α = 30° sur l’horizontale. L’autre extrémité de la ficelle est reliée à un ressort ( R ) de raideur k = 10 N.m-1 et de masse négligeable. On prendra g = 10 m.s-2La deuxième extrémité du ressort est fixée au sol. Les frottements sur le plan incliné et sur l’axe de la poulie seront négligés. On admettra que la ficelle ne glisse ne glisse pas dans la gorge de la poulie seront négligés. On admettra que la ficelle ne glisse pas dans la gorge de la poulie et que le centre d’inertie G de (S) se déplace sur la ligne de plus grande pente du plan. Le schéma de la machine est donné en figure ci-dessus.
A-1-a) Ecrire une relation entre m, g, α et l’allongement x0 du ressort lorsque le système est en équilibre.
b) Calculer la valeur numérique de x0 .
A-2– On provoque un déplacement supplémentaire a = 2 cm de (S)
vers le bas de la pente puis on l’abandonne sans vitesse initiale. Il prend alors un mouvement d’équation horaire: \(x(t) = 2.\cos \left( {\sqrt {\frac{k}{{m + \frac{{{J_\Delta }}}{{{r^2}}}}}} .t} \right)\)
Où x est l’écart du centre d’inertie de (S) à la position d’équilibre à un instant t quelconque (x en cm).
A-2-1– Donner l’expression de la période propre T0 des oscillations du solide (S) en fonction de m, r, k et JΔ .
A-2-2– Exprimer le moment d’inertie JΔ en fonction de la période propre T0 .
En mesurant la durée de 10 oscillations, on trouve 20 seconde.
Calculer numériquement JΔ . Prendre \({\pi ^2} = 10\)
A-2-3– Donner l’équation horaire du mouvement de rotation de la poulie.
B. Un oscillateur électrique
Un circuit LC est constitué d’une bobine d’inductance L et de résistance négligeable branché au bornes d’un condensateur de capacité C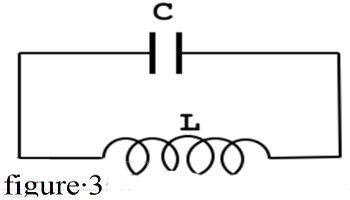
et de charge initiale q0 . Le schéma du circuit est donné en figure 3 ci-contre.
et de charge initiale q0 . Le schéma du circuit est donné en figure 3 ci-contre.B.1. Donner l’expression de la tension uAB aux bornes de chacun des deux dipôles.
B.2. En déduire l’équation différentielle vérifiée par la charge q(t) du condensateur.
N.B On rappelle que l’intensité du courant est la dérivée première de la charge par rapport au temps.
B.3. Pour L = 2,29 10-4 H, calculer la capacité C du condensateur qu’il faut pour que la charge q oscille avec une fréquence f = 105 MHz. On rappelle que 1 MHz = 106 Hz.
Exercice 3 : Phénomènes corpusculaires et ondulatoires
A– Phénomènes ondulatoires
L’extrémité O d’une ficelle de longueur convenable est attachée à un vibreur de période T = 10-2 s. les amortissements et la réflexion des ondes sont négligeables. La longueur d’onde λ de l’onde vaut 5 cm.
A.1. Calculer la célérité v de la propagation de l’onde.
A.2. On éclaire la ficelle à l’aide d’un stroboscope de fréquence fe négligeable.
a) Déterminer la plus grande fréquence f0 pour laquelle on voit une ficelle immobile.
a) La fréquence des éclaires du stroboscope prend la valeur f1 = 99 Hz. Qu’observe t’on?
A.3. L’équation horaire d’un point M de la ficelle situé à 30 cm de la source O est \(x(t) = 5.\cos (200.\pi t)\) en mm.
En déduire l’équation horaire de la source O.
B. Effet photoélectrique
On éclaire la cathode d’une cellule photoélectrique à l’aide d’une lumière monochromatique de longueur d’onde λ convenable. La variation de l’intensité i du courant photoélectrique en fonction de la tension entre l’anode et la cathode est consignée dans le tableau ci-dessous:
| \(U(V)\) | -0,8 | -0,4 | 0 | 0,22 | 0,6 | 1,1 | 2 | 3 | 4 | 5 |
| \(I(\mu A)\) | 0 | 1 | 1,65 | 2 | 3 | 4 | 5 | 5,2 | 5,3 | 5,3 |
Echelle: Abscisse 2 cm pour 1 V; Ordonnée: 2 cm pour 1µA.
B.2.a) Définir et déterminer le potentiel d’arrêt U0 .
b) Donner la valeur de l’intensité Is du courant de saturation.
B.3. Calculer la vitesse maximales des électrons à la sortie de la cathode.
On donne : charge élémentaire : e = 1,6 10-19 C
Masse de l’électron : me = 9,1 10-31 kg
Exercice 4 : Exploitation des résultats d’une expérience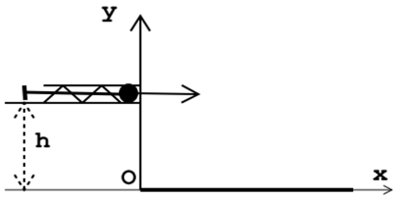
Une catapulte est constituée d’un piston enfilé dans un ressort de compression. L’ensemble peut coulisser à l’intérieur d’un tube cylindrique. Ce dispositif permet de lancer à partir d’une hauteur h, une bille (S) qu’on supposera ponctuelle, avec une même vitesse horizontal et de module v0=5m/s. Pour chaque valeur de h, on mesure l’abscisse xm du point d’impact de la bille sur le plancher horizontale sur la plancher (voir la figure 4 ci-dessus). On a obtenu le tableau de mesures suivant:
| h(cm) | 20 | 40 | 60 | 80 | 100 | 120 | 140 |
| \({x_m}(m)\) | 1,00 | 1,43 | 1,73 | 2,00 | 2,26 | 2,43 | 2,60 |
| \(x_m^2({m^2})\) | 1,00 | 2,00 | 3,00 | 4,00 | 5,1 | 5,9 | 5,8 |
4.1 Tracer sur papier millimètre la courbe \(x_m^2 = f(h)\)
Echelle : Abscisse : 1 cm ↔ 10 cm; ordonné : 1 cm ↔ 1 m2 .
Quelle est la forme de la courbe obtenue?
4.2.a) Etablir, lorsque la bille est lancée à partir d’une hauteur quelconque h, l’équation cartésienne de sa trajectoire, dans le repère indiqué sur le schéma.
On prendra pour instant initial, la date de départ de la bille. On négligera la résistance de l’air.
4.2.b) En déduire la relation suivante : \(x_m^2 = \frac{{2.v_0^2}}{g}.h\)
4.3. A partir de la courbe ci-dessus, déterminer une valeur expérimentale de l’accélération de la pesanteur g à l’endroit où s’effectue la manipulation.
