Probatoire
Physique
D
2010
Enoncés
Bonjour ! Groupe telegram de camerecole, soumettrez-y toutes vos préoccupations. forum telegram
Exercice 1: Optique
A. Les lentilles sphériques minces.
A.1. Comment reconnaître la nature (divergente ou convergente) d’une lentille mince par son aspect?
A.2. Qu’appelle-t-on distance focale d’une lentille?
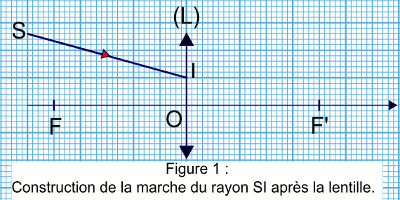
A.3. Construire sur la figure 1 de l’annexe ci-dessous, la marche du rayon SI à travers la lentille (L).
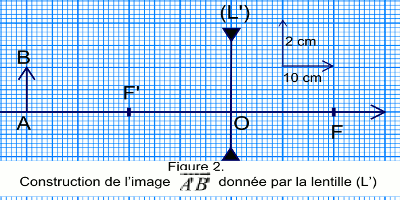
A.4. Un objet lumineux assimilable à une petite flèche verticale \(\overrightarrow {AB} \) de hauteur 2cm, est placé à 40 cm en avant d’une lentille divergente (L’), de distance focale f = -20 cm .
a. Construire sur la figure 2 de l’annexe ci-dessous, l’image \(\overrightarrow {A'B'} \) de \(\overrightarrow {AB} \) donnée par (L’).
b. Déterminer par calcul la position, la nature, le sens et la grandeur de \(\overrightarrow {A'B'} \)
B. Œil et instrument optique
B.1. Jules est un élève de votre classe. Il porte des lunettes dont les verres sont des lentilles convergentes.
a. Quel est le défaut des yeux de Jules?
b. Le punctum remotum (PR) de chaque œil de Jules est-il en avant ou en arrière de la rétine?
c. La lentille correctrice forme au (PR) de l’œil, l’image des objets situés à l’infini. En utilisant la formule de conjugaison, déterminer la distance maximale de vision distincte D de l’œil gauche de Jules, sachant que la lentille correctrice de cet œil a pour vergence C1 = 0,5δ.
On négligera la distance entre l’œil et le verre.
B.2. L’objectif et l’oculaire d’une lunette astronomique sont assimilables a des lentilles convergentes de distances focales respectives f1 et f2 .
a. A quoi sert une lunette astronomique?
b. Un œil normal observe un astre à travers cette lunette. Celle-ci est réglée pour une vision à l’infini.
- Que signifie « régler un instrument d’optique pour une vision à l’infini »?
- Où est située l’image de l’astre donnée par l’objectif?
A. Les lentilles sphériques minces.
A.1. Comment reconnaître la nature (divergente ou convergente) d’une lentille mince par son aspect?
A.2. Qu’appelle-t-on distance focale d’une lentille?
A.3. Construire sur la figure 1 de l’annexe ci-dessous, la marche du rayon SI à travers la lentille (L).
A.4. Un objet lumineux assimilable à une petite flèche verticale \(\overrightarrow {AB} \) de hauteur 2cm, est placé à 40 cm en avant d’une lentille divergente (L’), de distance focale f = -20 cm .
a. Construire sur la figure 2 de l’annexe ci-dessous, l’image \(\overrightarrow {A'B'} \) de \(\overrightarrow {AB} \) donnée par (L’).
b. Déterminer par calcul la position, la nature, le sens et la grandeur de \(\overrightarrow {A'B'} \)


B. Œil et instrument optique
B.1. Jules est un élève de votre classe. Il porte des lunettes dont les verres sont des lentilles convergentes.
a. Quel est le défaut des yeux de Jules?
b. Le punctum remotum (PR) de chaque œil de Jules est-il en avant ou en arrière de la rétine?
c. La lentille correctrice forme au (PR) de l’œil, l’image des objets situés à l’infini. En utilisant la formule de conjugaison, déterminer la distance maximale de vision distincte D de l’œil gauche de Jules, sachant que la lentille correctrice de cet œil a pour vergence C1 = 0,5δ.
On négligera la distance entre l’œil et le verre.
B.2. L’objectif et l’oculaire d’une lunette astronomique sont assimilables a des lentilles convergentes de distances focales respectives f1 et f2 .
a. A quoi sert une lunette astronomique?
b. Un œil normal observe un astre à travers cette lunette. Celle-ci est réglée pour une vision à l’infini.
- Que signifie « régler un instrument d’optique pour une vision à l’infini »?
- Où est située l’image de l’astre donnée par l’objectif?
Exercice 2 : Energie électrique
A. Production du courant électrique
Une batterie d’accumulateurs au plomb comporte 6 élément en série, de f.é.m. e = 2V chacun.
a. Quelle est la f.é.m. de cette batterie?
b. La quantité d’électricité qui à traversé cette batterie lors de sa charge est Qc = 50Ah. Combien de temps cette batterie peut-elle fonctionner en fournissant un courant d’intensité I = 2A, si son rendement en quantité ηQ vaut 0,8?
c. Écrire les équations des réactions qui ont lieu aux électrodes lors de ce fonctionnement sachant que les deux couples en présence sont : PbO2 /Pb2+ et Pb2+ /Pb.
d. Citer deux règles de protection des batteries d’accumulateurs au plomb.
B. Bilan énergétique dans un circuit électrique
Un générateur de force électromotrice E = 12V et de résistance interne r = 1,0Ω alimente un moteur à courant continu, de force contre électromotrice E’ = 9,0V et de résistance interne r’. L’intensité du courant fourni par le générateur est I = 1,5A.
B.1. Calculer la puissance totale générée par le générateur, la puissance dissipée par ce dernier par effet joule, et la puissance électrique qu’il fournit au circuit extérieur.
B.2. Que vaut le rendement du générateur?
B.3. Calculer la puissance électrique reçue par le moteur, la puissance dissipé par ce dernier par effet joule, et la puissance mécanique qu’il fournit.
En déduire la résistance interne r’ du moteur.
Exercice 3 : Energie mécanique
A. Lancer de « poids »
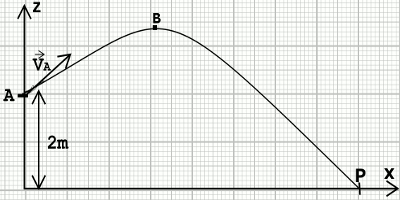
Au cours d’une compétition de lancer de « poids », ce dernier quitte la main d’un athlète en A, à une hauteur H = 2,0m du sol avec une vitesse \({\overrightarrow v _A}\) de module vA = 8,0 m.s-1 . Le « poids » est une sphère pleine de masse m = 2Kg, qui sera assimilé à un point matériel. Il décrit au cours de son mouvement une trajectoire parabolique représentée sur la figure ci-dessous; l’échelle de la figure étant : 1cm ↔ 1cm.
A.1. Faire l’inventaire des forces qui s’exercent sur le « poids » au cours de son déplacement.
On négligera la résistance de l’air et la poussée d’Archimède.
A.2. En appliquant le théorème de l’énergie cinétique, calculer le module de la vitesse \({\overrightarrow v _B}\) du « poids » au sommet B de sa trajectoire. On prendra g = 10N.Kg-1 .A.3 Le système {« poids » + Terre} est t’il conservatif?
Justifier la réponse.
A.4. On choisit le niveau de référence de l’énergie potentielle de pesanteur sur le plan horizontal contenant le point A.
a. Comparer l’énergie mécanique E1 du système {« poids »-Terre} au départ du « poids » en A à celle E2 , à l’arrivée en P.
b. En décuire l’énergie cinétique du « poids » lorsqu’il arrive au point P.
B. Rotation d’une roue de bicyclette.
Henri retourne son vélo et pose sur le sol, les roues en l’air.après avoir tracé un repère sur la roue arrière, il applique sur celle-ci une force en un point de sa périphérie, qui la met en rotation autour de son axe Δ. La vitesse angulaire initiale de rotation étant ω0 = 4,71rad/s, Henri constate que la roue tourne de moins à moins vite, et s’immobilise après avoir effectué 10,5 tours.
B.1. Faire le bilan des forces qui s’exerce sur la roue au cour de sa rotation.
B.2. En appliquant le théorème de l’énergie cinétique, calculer somme algébrique des travaux des forces qui s’opposent à la rotation de la roue.
B.3. On suppose que les forces de la question B.2. à un couple résistant de moment constant MΔ par rapport à l’axe de rotation de la roue. Déterminer MΔ .
On donne: Moment d’inertie de la roue par rapport à l’axe Δ JΔ = 2,5Kg.m2 .