Partie A : Évaluation des ressources (15 points)
Exercice I / (5 points)
1.) Résolvons dans C l’équation : z2+2− 2i√3=0
z2=−2+ 2i√3= (1+i√3)2
{z=1+i√3z=−1−i√3 0,75 pt
2.a) Donnons les éléments caractéristiques de s
s est la similitude directe de centre O, de rapport 2 et d’angle −π3 0,75 pt
2.b) Déterminons les images par s des points A et B. 0,5 pt
On a : (1−i√3)zA=4 et (1−i√3)zB=−4, donc s(A)=F et s(B)=G
3.a) Déterminons une équation de l’image (ε′)de (ε) par la similitude s 1 pt
O est le centre de (ε′) qui est une ellipse d’équation x2a2+y2b2=1, d’où c=OF=4 ; e=ca ; donc a=8 et b=√a2−c2 =√48
Donc une équation de (ε′) est x264+y248=1
3.b) Construisons (ε′) puis (ε) dans le même repère. 1 pt
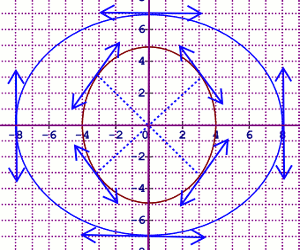On peut remarquer que l’ellipse (ε) est l’image de l’ellipse (ε′) par la similitude s−1 qui est de centre O, de rapport 12 et d’angle π3
4) Déterminons la probabilité pour que Aicha choisisse deux points de l’axe focale de (ε′)
Il y a trois de ces cinq points qui appartiennent à l’axe focale de (ε′), donc la probabilité demandée est : 1 pt
P=A23A25=310
Exercice 2 / 5 pts
1.a) Démontrons que Ek est un sous espace vectoriel de E 1 pt
• f(→O)=→O =k→O, donc →O∈Ek et alors Ek≠ϕ
• Soient →u, →v∈Ek, λ∈R, montrons que →u+→v∈Ek et que λ→u∈Ek.
f(→u+→v)=f(→u) +f(→v)=k→u+ k→v=k(→u+→v), donc →u+→v∈Ek
f(λ→u)=λ(k→u) =k(λ→u) donc λ→u∈Ek
Remarque : on peut aussi démontrer que Ek= ker(f−kIdE)
1.b) Démontrons que →u∈Imf si et seulement si →u∈E2. 1 pt
• Soit →u∈E2 :
→u∈E2⇒ f(→u)=2→u ⇔→u= f(12→u); donc →u∈Imf
• Soit →u∈Imf, il existe →v∈E tel que →u=f(→v), ainsi f(→u)=f∘f(→v) d’où f(→u)=2f(→v) =2→u donc →u∈E2
Conclusion →u∈Imf si et seulement si →u∈E2
2.a) Démontrons que f(→i)=2→i, f(→j)=2→j et f(→k)= −2→i+2→j.
On a :
f(→i)+f(→j)= 2→i+2→j:(1)
f(→i)−f(→j)= 2→i+2→j:(2)
f(→i)−f(→j) +f(→k)=→0:(3)
(1) + (2) implique que f(→i)=2→i
(1) - (2) implique que f(→j)=2→j
(3) implique que f(→k)=f(→j) −f(→i)=−2→i+ 2→j
2.b) Donnons la matrice M dans la base (→i,→j,→k) 0,5 pt
M=(20−2022000)
2.c) Démontrons que f∘f=2f 0,5 pt
M×M= (40−4044000)= 2(20−2022000)
2.d) Déterminons l’image Imf de f. Précisons une de ses bases, le noyau de Kerf
Soit →u=x→i+ y→j+z→k
→u=∈Kerf ⇔f(→u)=→0 ce qui implique que {2x−2z=02y+2z=0 soit {x=zy=−x soit →u=x(→i−→j +→k) donc Kerf est la droite vectorielle de base (→i−→j+→k)
2.e) Déterminons l’image Imf de f et précisons ses bases
Imf est engendré par les vecteurs f(→i), f(→j) et f(→i) et comme f(→i)=2→i, f(→j)=2→j et f(→k)=−2→i+2→j, alors Imf est engendrée par →i et →j. Or dimImf=dimE −dimKerf=2 donc Imf est le plan vectoriel de base (→i,→j), qui est aussi le plan d’équation z=0.
Exercice 3 / 5 pts
1) Démontrons que f″(x)+2f′(x) +2f(x)=0 0,5 pt
En effet, f′(x)=−excosx −e−xsinx et f″(x)=2e−xsinx en substituant ces fonctions dans l’équation initiale, nous avons f″(x)+2f′(x) +2f(x)=0
2) Étudions les variations de f et dressons son tableau de variations. 1,25 pt
La fonction f est définie et dérivable sur [0,2π]
f(0)=1, f(2π)=2e−2π
Dans [0,2π], f′(x)=0 ⇒x=3π4 ou x=7π4
f′(x)≥0⇔ x∈[3π4;7π4], Ainsi la fonction f est croissante sur [3π4;7π4], décroissante sur [0;3π4] et [7π4;2π].
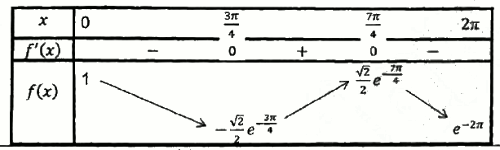3.a) Démontrons que e−x≤f(x) ≤e−x 0,5 pt
Soit x∈[0;2π], alors −1≤cosx≤1 et e−x≻0 donc −e−x≤f(x)≤e−x.
3.b) Déterminons les coordonnées des points d’intersection de (Cf) avec les courbes y=−e−x et y=e−x. 0, 75 pt
Soit x∈[0;2π]
f(x)=e−x ⇔cosx=1⇒ x=0 ou x=2π. Donc les coordonnées des points d’intersection de (Cf) avec la courbe y=e−x sont (0;1) et (2π;e−2π)
f(x)=−e−x⇔ cosx=−1⇒ x=π donc la courbe (Cf) rencontre la courbe d’équation y=−e−x en un point de coordonnées (π;e−π)
4.) Traçons dans le même repère, les courbes d’équations y=−ex et y=−e−x puis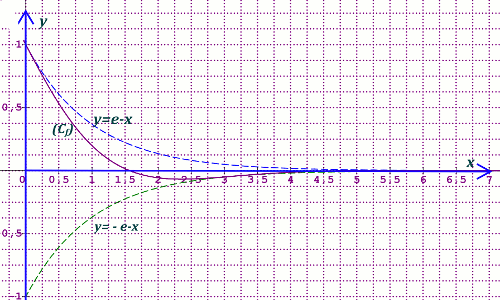 (Cf) sur [0;2π]
Les courbes d’équations y=e−x et y=−e−x sont symetriques par rapport à l’axe des abscisses. Celle d’équation y=e−x se déduit de celle de la fonction y=ex par symétrie par rapport à l’axe (Oy)
5. Calculons l’aire de la partie du plan délimitée par (Cf) et la courbe d’équation y=e−x sur [0;2π] 1 pt
En unité d’aire, cette aire :
2π∫0(e−x−f(x))dx =[e−x(−1+12(− sinx+cosx)]2π0 =12(1−e−2π)
Cette aire en cm3 est 4(1−e−2π)
Partie B : Évaluation des compétences / 5 pts
1) Déterminons en combien d'années le gisement A va s'épuiser.
Désignons par An la quantité en milliards de m3 de gaz extraite à la nieme années après l'inauguration : n étant un nombre entier naturel non nul. Tant que le gisement reste suffisamment fourni.
on a A1=5,01 et An+1=An+1+0,75.75. D'où An+1=0,75n+4,26
Au bout de ces n années, la quantité totale de gaz extraite du gisement A est : Qn=A1+...+An =n(A1+An)2 =0,375n2+4,635n avec Qn≤100 ⇒0,375n2+ 4,635n≤100 c'est-à-dire que pour n∈ ]0;−927+√6859329150] avec −927+√6859329150 ≈11,28
Comme Q11=0,375(11)2 +4,635(11)=96,36, le reste du gisement A alors vidé à la 12e année. Le gisement A va donc s'épuiser en 12 ans.
2) Déterminons le nombre d'années d'extraction pour épuiser le gisement B.
q′(t)=12t+1 +0,02t⇒q(t)= 12ln(2t+1)+0,01t2 +c, c étant une constante réelle. q(0)=0 soit q(t)=12ln(2t+1) +0,01t2
Le gisement B va s'épuiser lorsque q(t)=100.
La fonction q est continue et strictement croissante sur ]0;+∞[. De plus 100 est entre q(98)≈98,69 et q(99)≈100,65; donc l'équation q(t)=100 admet une unique solution entre 98 et 99.
Conclusion : Le gisement B va s'épuiser à la 99° année.
3) Déterminons le nombre d'années après l'inauguration pour vider le gisement C de son contenu.
on a : q′(t)q(t)=...= q′(t)q(t)=5,015,01 =1
D'où q(t)=q′(t).
c étant une constante réelle.
q(1)=5,01⇒ ce=5,01⇒ c=5,01e−1
Ainsi q(t)=5,01e(t−1)
Le gisement C va s'épuiser lorsque q(t)=100, soit 5,01e(t−1)=100
t=1+ln(10000501) ≈3,99
Donc le gisement C va se vider 4 ans après l'inauguration.
