Correction exercice I
1. \(\left\{ \begin{array}{l}{Z_A} \ne {Z_B}\\{Z_B} \ne {Z_C}\end{array} \right.\) donc les points A, B et C sont tels que : \(\left\{ \begin{array}{l}A \ne B\\B \ne C\end{array} \right.\)
\(mes\left( {\widehat {\overrightarrow {BC} ;\overrightarrow {BA} }} \right)\) \( = \arg \left( {\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right)\)
Calculons \({\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}}\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}} = \) \(\frac{{ - 1 + i\sqrt 3 - 2}}{{ - 1 - i\sqrt 3 - 2}}\) \( = \frac{1}{2} - \) \(i\frac{{\sqrt 3 }}{2}\)
Posons \(\arg \left( {\frac{1}{2} - i\frac{{\sqrt 3 }}{2}} \right)\) \( = \alpha \)
On a \(\left\{ \begin{array}{l}\cos \alpha = \frac{1}{2}\\\sin \alpha = - \frac{{\sqrt 3 }}{2}
\end{array} \right.\) \( \Rightarrow \alpha = - \frac{\pi }{3}\)
La mesure principale de l’angle orienté \(\left( {\widehat {\overrightarrow {BC} ;\overrightarrow {BA} }} \right)\) est \( - \frac{\pi }{3}\).
2. Donnons une interprétation \(\left| {\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right|\)
On a : \({Z_B} \ne {Z_C}\); ce qui justifie l’existence du \(\left| {\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right|\)
\(\left| {\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right|\) \( = \frac{{AB}}{{BC}}\)
3. \(\left| {\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right|\) \( = \left| {\frac{{1 - i\sqrt 3 }}{2}} \right|\) \( = 1\) \(1 \Rightarrow AB\) \( = BC\)
Correction exercice II
On considère les points A, B, C et D d’affixes respectives \(5 + i\); \( - 2\); \(1 + i\) et \( - 4 - 2i\)
1. Traçons les droites (AD) et (BC). 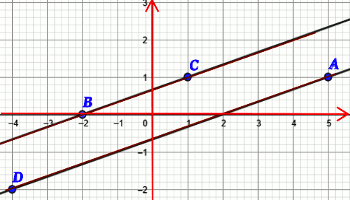 2. Démontrons que les droites (AD) et (BC) sont parallèles.
2. Démontrons que les droites (AD) et (BC) sont parallèles.
\({Z_A} \ne {Z_B}\) et \({Z_D} \ne {Z_C}\) alors \(A \ne B\) et \(D \ne C\)
Calculons \(\frac{{{Z_D} - {Z_A}}}{{{Z_C} - {Z_B}}}\)
\(\frac{{{Z_D} - {Z_A}}}{{{Z_C} - {Z_B}}}\) \( = \frac{{ - 9 - 3i}}{{3 + i}}\) \( = \frac{{ - 3\left( {3 + i} \right)}}{{3 + i}}\) \( = - 3\) \( \in \) \( \mathbb{R^*}\)
Ainsi, les droites (AD) et (BC) sont parallèles.
Correction exercice III
On considère les points A, B et C d’affixes respectives \(2 + i\sqrt 3 \); \( - 1\) et \(11 + 4i\sqrt 3 \).
Démontrons que les points A, B et C sont alignés.
En effet, \(A \ne B\) et \(B \ne C\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}} = \) \(\frac{{3 + i\sqrt 3 }}{{12 + 4i\sqrt 3 }}\) \( = \frac{1}{4} \in \) \( \mathbb{R^*}\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}} \in \) \( \mathbb{R^*}\)
Ainsi, les points A, B et C sont alignés.
Correction exercice IV
On considère les points A, B, C et H d’affixes respectives \( - 3 - i\);\( - 2 + 4i\); \(3 - i\) et \( - 2\).
1) Traçons les droites (AH) et (BC). 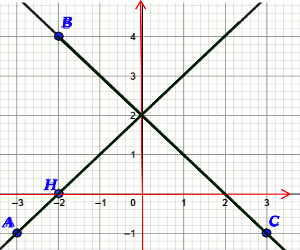 2) Démontrons que les droites (AH) et (BC) sont perpendiculaires
2) Démontrons que les droites (AH) et (BC) sont perpendiculaires
En effet, \(A \ne H\) et \(C \ne B\),
\(\frac{{{Z_B} - {Z_C}}}{{{Z_H} - {Z_A}}}\) \( = \frac{{10i}}{2}\) \( = 5i\) \( \in \) \(i \mathbb{R^*}\)
Donc les droites (AH) et (BC) sont perpendiculaires.
Correction exercice V
Dans le plan complexe rapporté au repère orthonormé (O, I, J), on considère les points A, B, C et D d’affixes respectives \(−2? \); \(7 – ?\) et \(8 + 2?\) et \(−1 + 5?\).
a) Plaçons les points A, B, C et D dans le repère. 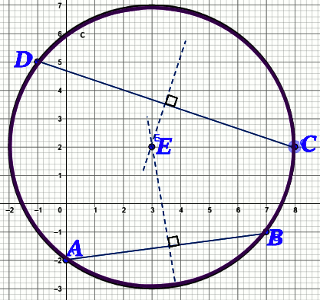 b) Démontrons que les points A, B, C et D sont cocycliques.
b) Démontrons que les points A, B, C et D sont cocycliques.
\({Z_B} \ne {Z_A}\) et \({Z_B} \ne {Z_D}\)
Calculons \(\frac{{{Z_D} - {Z_A}}}{{{Z_B} - {Z_A}}}\) et \(\frac{{{Z_D} - {Z_C}}}{{{Z_B} - {Z_C}}}\)
\(\frac{{{Z_D} - {Z_A}}}{{{Z_B} - {Z_A}}} = i\) et \(\frac{{{Z_D} - {Z_C}}}{{{Z_B} - {Z_C}}}\) \( = - 3i\)
\(\frac{{\frac{{{Z_D} - {Z_C}}}{{{Z_B} - {Z_C}}}}}{{\frac{{{Z_D} - {Z_C}}}{{{Z_B} - {Z_C}}}}}\) \( = \frac{i}{{ - 3i}}\) \( = - \frac{1}{3}\) \( \in \) \( \mathbb{R^*}\)
Donc les points A, B, C et D sont cocycliques.
Correction exercice VI
Dans le plan complexe rapporté à un repère orthonormé (O, I, J), on considère les points A, B et C d’affixes respectives \(1 + ?\) ; \(3\) et \(3 + 5?\).
a) Plaçons les points A, B et C dans le repère (O, I, J).
i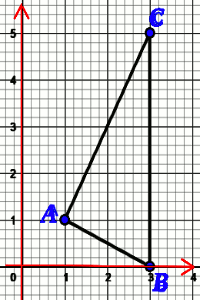 b) Démontrons que le triangle ABC est rectangle en A.
b) Démontrons que le triangle ABC est rectangle en A.
\(A \ne B\) et \(C \ne A\)
\(\frac{{{Z_B} - {Z_A}}}{{{Z_C} - {Z_A}}}\) \( = \frac{{2 - i}}{{2 + 4i}}\) \( = - \frac{1}{2}i\) \( \in \) \( i\mathbb{R^*}\)
Donc le triangle ABC est rectangle en A
2. On considère les points A, B et C d’affixes respectives \(−3 + 2?\) ; \(−2 − 3?\) et \(3 − 2?\) Démontrons que le triangle ABC est rectangle isocèle en B.
\(A \ne B\) et \(C \ne B\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}}\) \( = i \in \) \( \mathbb{R^*}\)
Donc le triangle est rectangle isocèle en B.
3. On considère les points A, B et C d’affixes respectives\( - 1 + i\sqrt 3 \); 2 et\( - 1 - i\sqrt 3 \). Démontrons que le triangle ABC est équilatéral.
\(A \ne B\) et \(C \ne B\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}} = \) \(\frac{1}{2} - i\frac{{\sqrt 3 }}{2}\) \( = \cos \left( { - \frac{\pi }{3}} \right)\) \( + i\sin \cos \left( { - \frac{\pi }{3}} \right)\) \( = {e^{ - i\frac{\pi }{3}}}\)
\(\frac{{{Z_A} - {Z_B}}}{{{Z_C} - {Z_B}}} = \) \({e^{ - i\frac{\pi }{3}}}\) donc ABC est un triangle équilatéral.
Correction exercice VII
Soient A, B, C, D quatre points d'affixes respectifs : \( - 1 + i\), \( - 1 - i\), \(2i\) et \(2 - 2i\)
1) Etudions la nature des triangles ABC et BCD.
• Pour le triangle ABC
\(\frac{{{Z_C} - {Z_A}}}{{{Z_B} - {Z_A}}}\) \( = \frac{{1 + i}}{{2i}}\) \( = - \frac{1}{2} + \frac{1}{2}i\)
\(\arg \left( {\frac{{{Z_C} - {Z_A}}}{{{Z_B} - {Z_A}}}} \right)\) \( = \arg \left( { - \frac{1}{2} + \frac{1}{2}i} \right)\) \( = \frac{{3\pi }}{4}\)
\(AB = \) \(\sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \) \( = 2\sqrt 2 \)
\(AC = \sqrt 2 \)
\(BD = \sqrt {10} \)
Alors le triangle ABC est quelconque.
• Pour le triangle BCD
\(\frac{{{Z_D} - {Z_B}}}{{{Z_C} - {Z_B}}}\) \( = - i\)
\(\arg \left( {\frac{{{Z_D} - {Z_B}}}{{{Z_C} - {Z_B}}}} \right)\) \( = \arg \left( { - i} \right)\) \( = - \frac{\pi }{2}\)
\(BC = \sqrt {10} \)
\(CD = 5\sqrt 2 \)
\(BD = \sqrt {10} \)
Alors le triangle BCD est rectangle et isocèle en B.
2) Démontrons que les points A, B, C et D appartiennent à un même cercle dont on déterminera le centre et le rayon.
Soit \(\Omega \left( {x;y} \right)\) les coordonnées du centre de ce cercle. Les points A, B, C et D appartiennent à un même cercle si :
\(d(A;\Omega ) = \) \(d(B;\Omega ) = \) \(d(C;\Omega ) = \) \(d(D;\Omega ) = r\)
\(d(A;\Omega ) = d(B;\Omega )\)
\(\sqrt {{{\left( {{x_\Omega } - {x_A}} \right)}^2} - {{\left( {{y_\Omega } - {y_A}} \right)}^2}} \) \( = \) \(\sqrt {{{\left( {{x_\Omega } - {x_B}} \right)}^2} - {{\left( {{y_\Omega } - {y_B}} \right)}^2}} \)
Apres simplification, nous avons
\( - 2y = 2y\) \( \Rightarrow y = 0\)
\(d(C;\Omega ) = d(D;\Omega )\)
\(\sqrt {{{\left( {{x_\Omega } - {x_C}} \right)}^2} - {{\left( {{y_\Omega } - {y_C}} \right)}^2}} \) \( = \) \(\sqrt {{{\left( {{x_\Omega } - {x_D}} \right)}^2} - {{\left( {{y_\Omega } - {y_D}} \right)}^2}} \)
En remplaçant \(y = 0\) par sa valeur dans l’équation ci-dessus, on a :
\( - 4x + 4 = 0\) \( \Rightarrow x = 1\)
D’où \(\Omega \left( \begin{array}{l}1\\0\end{array} \right)\)
\(d(A;\Omega ) = \) \(d(B;\Omega ) = \) \(d(C;\Omega ) = \) \(d(D;\Omega ) = r\)
\(r = \sqrt 5 \)
D’où les points A, B, C et D qui appartiennent à un même cercle de centre \(\Omega \left( \begin{array}{l}1\\0\end{array} \right)\) et de rayon \(r = \sqrt 5 \)

