I. Module :

Dans le plan rapporté à un repère $\left( {O;\overrightarrow i ;\overrightarrow j } \right)$; plaçons le point M de Z dont l'affixe est $Z = a + ib$ $\Rightarrow M\left( \begin{array}{l}a\\b\end{array} \right)$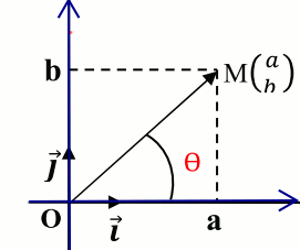
$\left\| {\overrightarrow {OM} } \right\| =$ $d(OM) =$ $\sqrt {{a^2} + {b^2}}$

I.1 Définition

Soit $Z = a + ib$ un nombre complexe. On appelle module de Z, le nombre réel positif ou nul noté : $\left| Z \right|$ tel que $\left| Z \right| =$ $\sqrt {{a^2} + {b^2}}$
Si M est le point image de Z alors $\left| Z \right| =$ $d(OM) =$ $\sqrt {{a^2} + {b^2}}$

I.2 Propriétés

P.1 $\left| Z \right|$ est toujours positif

P.2 $\left| {Z \times Z'} \right|$ $= \left| Z \right| \times \left| {Z'} \right|$

P.3 $\left| Z \right| = \left| {\overline Z } \right|$

P.4 $\left| Z \right| = 0$ $\Rightarrow Z = 0$

P.5 $\left| {Z + Z'} \right|$ $\le \left| Z \right| + \left| {Z'} \right|$ Inégalité triangulaire

P.6 $\left| {\frac{Z}{{Z'}}} \right| =$ $\frac{{\left| Z \right|}}{{\left| {Z'} \right|}}$ avec $Z' \ne 0$

P.7 $\left| {\frac{a}{{Z'}}} \right| =$ $\frac{a}{{\left| {Z'} \right|}}$ avec $Z' \ne 0$ et $a \in R$

P.8 $\left| {{Z^n}} \right| =$ ${\left| Z \right|^n}$ avec $n \in N$

II. Argument 

II.1 Définition

En observant la figure précédente, représentant un triangle rectangle d’angle $\theta$, on a :
$\cos \theta =$ $\frac{a}{{\sqrt {{a^2} + {b^2}} }}$
$\sin \theta =$ $\frac{b}{{\sqrt {{a^2} + {b^2}} }}$

Soit Z est un nombre complexe de module $\left| Z \right|$ ( avec $\left| Z \right| \ne 0$). On appelle argument de Z, le nombre réel noté $\theta$ ou $\arg (Z)$ tel que :

$\left\{ \begin{array}{l}\cos \theta = \frac{a}{{\left| Z \right|}}\\\sin \theta = \frac{b}{{\left| Z \right|}} \end{array} \right.$

Le cercle de référence trigonométrique et le tableau des angles trigonométriques sont nécessaires à connaître pour le calcul des arguments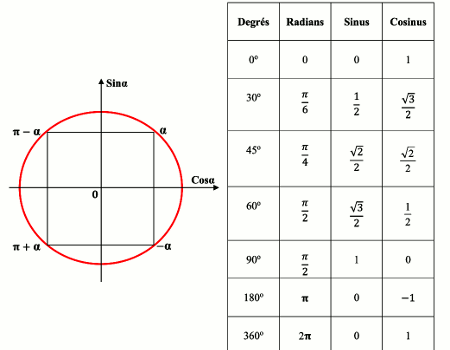

II.2 Propriétés

Soient Z et Z’ deux nombres complexes d’arguments respectifs $\arg (Z)$ et $\arg (Z’)$

P.1 $\arg (Z \times Z') =$ $\arg (Z) +$ $\arg (Z')$

P.2 $\arg (\frac{Z}{{Z'}}) =$ $\arg (Z) -$ $\arg (Z')$

P.3 $\arg ({Z^n}) =$ $n.\arg (Z)$

P.4 $\arg (\overline Z ) =$ $- \arg (Z)$

P.5 $\arg (\frac{a}{Z}) =$ $- \arg (Z)$ avec $Z \ne 0$