Filière : Raffinage et pétrochimie
Exercice 1. (Exploitation des résultats d’une expérience)
Prendre g = 10m/s2. Un solide (s) est lancé avec une vitesse initiale \({\overrightarrow V _0}\) à partir du sommet d’un plan incliné d’un angle \(\alpha = {30^o}\) sur l’horizontale. Le tableau ci-dessus donne les positions successives Gi de son centre d’inertie au cours du temps.
| ti(s) | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| Gi | G1 | G2 | G3 | G4 | G5 | G6 |
| Xi(cm) | 0 | 16 | 36 | 60 | 88 | 120 |
Dresser le tableau donnant la valeur de la vitesse VG du centre d’inertie du solide aux date \({t_i}\) avec \(0 \le i \le 4\).
On admettra que : \({V_G}_{_i} = \) \(\frac{{d\left( {{G_{i - 1}},{G_{i + 1}}} \right)}}{{{t_{i + 1}} - {t_{i - 1}}}}\)
2 Tracer sur la figure 2 de l’annexe à remettre avec la copie, le graphe de \({V_G} = f(t)\).
Échelle : 2 cm \( \leftrightarrow \) 0,1 s et 2 cm \( \leftrightarrow \) 100 cm/s
3 Déduire de cette courbe :
a. La valeur V0 de la vitesse qu’a le centre d’inertie au départ.
b. La valeur de l’accélération du centre d’inertie du solide.
4 Par application du théorème du centre d’inertie (deuxième loi de Newton) au solide, déterminer la valeur de l’accélération dans l’hypothèse où le contact solide plan se fait sans frottements.
5 Comparer les vecteurs de l’accélération du centre d’inertie du solide obtenues en 3-b et 4. L’hypothèse prise pour le calcul de l’accélération en 4 était-elle justifiée ? Conclure.
Exercice 2.
Un électron pénètre avec une vitesse \(\overrightarrow {{V_0}} \) dans une zone de l’espace où règne un champ magnétique uniforme, horizontal \(\overrightarrow B \) . Les directions des vecteurs vitesses et champ magnétique sont indiquées sur la figure, la vitesse initiale \(\overrightarrow {{V_0}} \) est perpendiculaire au champ magnétique \(\overrightarrow B \). Le poids de l’électron est négligeable devant la force magnétique.
Données \(e = {1,6.10^{ - 19}}\) C, \({m_e} = {9,0.10^{ - 31}}\) kg , B = 3, 0mT, Rayon de la trajectoire R = 9, 0cm .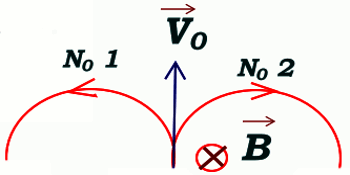 Répondre par vrai ou par faux aux questions suivantes :
Répondre par vrai ou par faux aux questions suivantes :
1 L’électron décrit l’arc de cercle N1 représenté sur la figure.
2 Son mouvement est uniforme et la valeur de sa vitesse est \(v = 4,8 \times {10^7}\) m/s.
3 L’accélération de l’électron est nulle.
La vitesse \({{V_0}}\) de l’électron est à présent parallèle au champ magnétique \(\overrightarrow B \).
4 Le mouvement de l’électron est rectiligne uniformément accéléré.
Exercice 3. (Phénomènes corpusculaires)
Le noyau d’un isotope de cobalt 60 se désintègre en donnant un nucléide stable et une particule \({\beta ^ - }\).
1 Écrire l’équation bilan de cette désintégration nucléide en précisant le nom, le nombre de masse et le numéro atomique du nucléide formé.
2 La demi-vie du cobalt 60 est T = 5, 3 ans. On considère un échantillon de masse M=10 g de minerai de teneur en cobalt 60 \(\tau = 20\% \)
a. Définir demi-vie d’un élément.
b. Calculer la masse de l’isotope dans ce minerai à l’instant t = 0 et au bout de 15,9 ans.
3 La particule β émise lors de la désintégration a une énergie E = 2MeV.
a. Calculer l’énergie au repos E0 de cette particule.
b. Calculer l’énergie cinétique (en MeV) de la particule, en déduire qu’elle est relativiste.
c. Calculer la quantité de mouvement de la particule (en MeV/c).
d. En déduire la vitesse de cette particule.
On donne : Masse de l’électron : \({m_e} = 9,11 \times {10^{ - 31}}\) kg; Charge élémentaire \(e = 1,6 \times {10^{ - 19}}\); \({N_A} = 6,22 \times \) \({10^{23}}mo{l^{ - 1}}\); Vitesse de la lumière : \(c = 3 \times {10^8}\) m/s ; log 2 = 0, 693 ;
Extrait du tableau de classification périodique : \({}_{25}Mn\), \({}_{26}Fe\), \({}_{28}Ni\), \({}_{29}Cu\), \({}_{30}Zn\).

