Situation problème:
Votre cousin, après son premier cours sur le spectre atomique, est curieux de savoir si on peut utiliser le spectre de la lumière émise par une étoile pour reconnaître certains de ses constituants.
Que lui répondez-vous?
Objectifs de cette leçon :
• Identifier un élément chimique à partir de son spectre d’émission ou d’absorption.
• Distinguer un spectre d’émission d’un spectre d’absorption.
• Appliquer la relation \(\Delta E = h.\upsilon \)
• Utiliser le spectre de la lumière émise par une étoile pour reconnaître certains de ses constituants.
Un spectre est l’ensemble des couleurs qui constituent une lumière.
Le spectre visible de la lumière blanche est constitué des sept couleurs de l’arc-en-ciel.
La spectroscopie est l’étude des diverses radiations monochromatiques composant la lumière émise ou absorbée par une substance.
Le spectroscope est un instrument permettant d’obtenir le spectre d’une lumière et de l’analyser.
I. Notion de spectre atomique
Le prisme décompose la lumière blanche (lumière du soleil) en sept radiations monochromatiques (une seule longueur d’onde)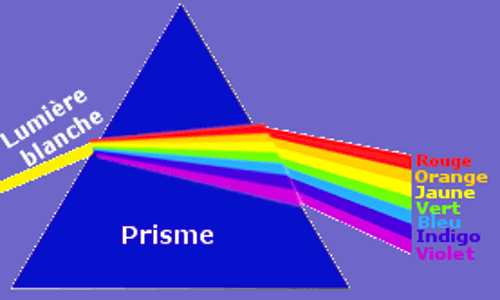 L’ensemble de ces radiations observées constitue le spectre de la lumière blanche.
L’ensemble de ces radiations observées constitue le spectre de la lumière blanche.
Le spectre de la lumière émise par une source lumineuse est appelée spectre d’émission, pour la lumière blanche, il est continu car on passe d’une radiation a une autre sans interruption.
Un atome peut absorber (absorption) ou émettre (émission) de l'énergie.
L'absorption de l’énergie cause le déplacement d'un électron à un niveau d'énergie supérieure.
I.1 Le spectre d’émission
Toute matière portée à une température élevée est source de rayonnement électromagnétique à spectre continu Une lampe à vapeur de sodium émet une lumière jaune composée d’un spectre de raies, en particulier deux raies jaunes intenses : c’est un spectre discontinu caractéristique de l’élément sodium.
Une lampe à vapeur de sodium émet une lumière jaune composée d’un spectre de raies, en particulier deux raies jaunes intenses : c’est un spectre discontinu caractéristique de l’élément sodium.
En d'autres termes, la détermination de la position des raies permet d'identifier l'atome qui est à l'origine de l'émission lumineuse.
I.2 Le spectre d’absorption
Si on fait passer de la lumière blanche dans la vapeur de sodium, on constate que le spectre d’absorption ainsi formée présente une raie noire à la place de la raie jaune précédente : la vapeur de sodium a absorbé uniquement la radiation jaune. Cette absorption est donc sélective.
Ceci montre que la lumière absorbée a la même longueur d’onde que la lumière émise par la vapeur de sodium excitée.
De manière générale, un atome n’absorbe que les radiations de fréquences égales à celles qu’il peut lui-même émettre.
II. Postulats de Bohr
Un postulat est une hypothèse vérifiée par ces conséquences.
Les postulats de Bohr reposent sur le modelé planétaire de l’atome, considéré comme un système solaire miniature.
L’électron y gravite en décrivant une trajectoire circulaire ou orbite (de rayon quantifié) autour du noyau. Chaque rayon correspondant à un niveau d’énergie \({E_n}\) de l’atome avec \(1 \le n \prec \infty \). On dit alors que l’énergie de l’atome est quantifiée.
Postulat 1 : L’énergie d’un atome ne peut prendre que certaines valeurs bien déterminées, celles-ci formant une suite discontinue.
A chacune de ces valeurs correspond un état appelé niveau d’énergie
• Si \(n=1\), l’électron est plus près du noyau et l’énergie atomique est la plus faible (énergie minimale) ;
• Si \(n \to \infty \), \({E_n} = 0\) et l’électron n’est plus lié au noyau et l’atome est dit ionisé.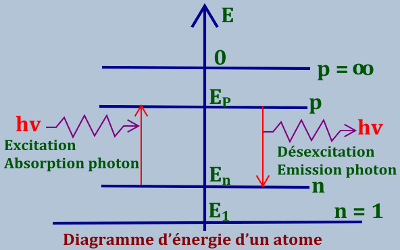 L’atone ne peut ni émettre, ni absorber de l’énergie tant que l’électron reste sur son orbite ou son énergie est constante, et l’énergie échangée entre l’électron de l’atome et l’extérieur se fait pas « sauts » et obéit à la relation :
L’atone ne peut ni émettre, ni absorber de l’énergie tant que l’électron reste sur son orbite ou son énergie est constante, et l’énergie échangée entre l’électron de l’atome et l’extérieur se fait pas « sauts » et obéit à la relation :
\(\Delta E = {E_p} - {E_n}\)
Avec \(n \prec p\)
Si \(\Delta E \succ 0\), il y’a absorption du photon et l’atome reçoit de l’énergie et se trouve dans un état excité, l’électron saute du niveau \(n\) au niveau \(p\)
Si \(\Delta E \prec 0\), l’atome cède de l’énergie à l’extérieur (émission de photon) se désexcite, cette désexcitation s’accompagne de l’émission d’un photon (énergie excédentaire)
L’énergie du photon est donnée par \(E = \frac{{h.\upsilon }}{\lambda }\)
Postulat 2 : Une transition est le passage d’un niveau d’énergie a une autre, les variations d’énergie ne peuvent prendre que des valeurs bien déterminées : on dit qu’elles sont quantifiées.
Dans le diagramme précèdent :
• Chaque ligne horizontale représente un niveau d’énergie de l’électron ;
• Une raie spectrale est représentée par une flèche verticale ;
• La longueur de cette flèche est proportionnelle à l’énergie du photon émis par la transition
III. Application des postulats de Bohr sur l’atome d’hydrogène
L’atome d’hydrogène H n’est formé que d’un seul électron liée à un proton. Son spectre d’émission révèle une série de raies dans le domaine du visible, d’autres séries dans l’ultraviolet (U.V) et infrarouge (I.R). Ces raies proviennent de la d’excitation de l’atome H d’un niveau d’énergie \({E_p}\) a un niveau d’énergie \({E_n}\) avec \({E_p} \succ {E_n}\), ceci produit une libération d’énergie \(\Delta E = {E_p} - {E_n}\) \( = h.\upsilon \)
La théorie de l’interaction proton-électron montre que la valeur d’un niveau d’énergie \({E_n}\) est donnée par la relation
\({E_n} = - \frac{{13,6}}{{{n^2}}}\)
Avec \(n\) un entier non nul représentant le nombre quantique principal et \({E_n}\) en électronvolt. (eV). Cette relation n’est valable que pour l’atome d’hydrogène.
L’énergie minimal à fournir à un atome H pris dans son état fondamental pour lui arracher son électron est appelée énergie d’ionisation et vaut \({E_1} = - \frac{{13,6}}{{{1^2}}}\) \( = - 13,6eV\)
Lorsqu’un photon d’énergie \(h.\upsilon \) arrive sur un atome H, deux phénomènes peuvent se produire :
• Si \({E_1} \prec h.\upsilon \), le photon est absorbé par l’atome H qui s’ionise.
• Si \({E_1} \succ h.\upsilon \), le photon n’est absorbé que si \(h.\upsilon \) correspond à une transition possible entre les deux niveaux.
Pour une transition \(p \to n\) avec \(p \succ n\), l’énergie libérée par l’atome H est donnée par la relation :
\(\Delta E = {E_p} - {E_n} = \) \( - \frac{{{E_1}}}{{{p^2}}} - \left( { - \frac{{{E_1}}}{{{n^2}}}} \right) = \) \({E_1}\left( {\frac{1}{{{n^2}}} - \frac{1}{{{p^2}}}} \right)\)
La longueur d’onde de la raie émise est définie par la relation
\({E_1}\left( {\frac{1}{{{n^2}}} - \frac{1}{{{p^2}}}} \right)\) \( = h\frac{C}{\lambda } \Rightarrow \frac{1}{\lambda } = \) \(\frac{{{E_1}}}{{hC}}\left( {\frac{1}{{{n^2}}} - \frac{1}{{{p^2}}}} \right)\)
La quantité \({R_H} = \frac{{{E_1}}}{{hC}} = \) \(1,0956 \times {10^7}{m^{ - 1}}\) est appelle constance de Rydberd
L’ensemble des transitions correspondant au niveau \(n\) comporte une même série de raies :
• Pour \(n = 1\) on a la série de Lyman
\(\frac{1}{\lambda } = {R_H}\left( {1 - \frac{1}{{{p^2}}}} \right)\) avec \(p \ge 2\),ils appartiennent au domaine de l’U.V
• Pour \( n = 2\), on a la série de raies de Balmer
\(\frac{1}{\lambda } = {R_H}\left( {\frac{1}{{{2^2}}} - \frac{1}{{{p^2}}}} \right)\) avec \(p \ge 3\), ils appartiennent au domaine de du visible pour la plupart
• Pour \( n = 3\), on a la série de Paschen
\(\frac{1}{\lambda } = {R_H}\left( {\frac{1}{{{3^2}}} - \frac{1}{{{p^2}}}} \right)\) avec \(p \ge 4\), ils appartiennent au domaine de l’I.R
• Pour \( n = 4\), on a la série de Brackett
\(\frac{1}{\lambda } = {R_H}\left( {\frac{1}{{{4^2}}} - \frac{1}{{{p^2}}}} \right)\) avec \(p \ge 5\), ils appartiennent au domaine de l’I.R
• Pour \( n = 5\), on a la série de Pfund
\(\frac{1}{\lambda } = {R_H}\left( {\frac{1}{{{5^2}}} - \frac{1}{{{p^2}}}} \right)\) avec \(p \ge 6\), ils appartiennent au domaine de l’I.R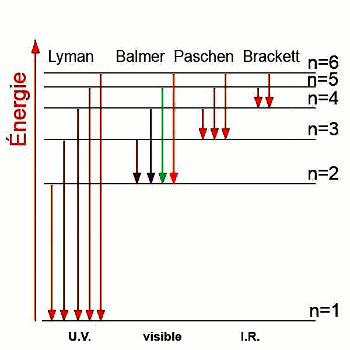
IV Énergie minimale et maximale de l’atome d’hydrogène
A l’état excite ( état instable), l’atome d’hydrogène peut céder l’énergie emmagasinée sous forme d’un photon lumineux d’énergie \(E = h\frac{C}{\lambda }\), on peut donc écrire \(E = f\left( {\frac{1}{\lambda }} \right)\)
L’énergie du photon est maximale si la longueur d’onde de la radiation émise est minimale
\({E_{\max }} = h\frac{C}{{{\lambda _{\min }}}} \Rightarrow \) \({\lambda _{\min }} = h\frac{C}{{{E_{\max }}}}\)
De même cette énergie sera minimale si la longueur d’onde de la radiation est maximale
\({E_{\min }} = h\frac{C}{{{\lambda _{\max }}}} \Rightarrow \) \({\lambda _{\max }} = h\frac{C}{{{E_{\min }}}}\)
Les transitions correspondantes varient avec la série, ainsi :
Dans la série de Lyman, \({E_{\max }}\) correspond à la transition \(\infty \to 1\) alors que \({E_{\min }}\) correspond à la transition \(2 \to 1\);
Dans la série de Balmer, \({E_{\max }}\) correspond à la transition \(\infty \to 2\) alors que \({E_{\min }}\) correspond à la transition \(3 \to 2\).

