Partie A : Évaluation des ressources (15 points)

Exercice 1 : 5,5 points (C) / 4 points (E)

I- (Série C exclusivement)
1. Démontrons que (D) passe par au moins un point M dont les coordonnées sont des nombres entiers relatifs. 0,25 pt
Soit \(M\left( {x;y} \right)\) un point du plan.
\(M \in \left( D \right)\) équivaut à \(y = \frac{{65}}{{16}}x - \frac{5}{{16}}\) équivaut à \(65x - 16y = 5\). Et puisque PGCD(65 ; 16) = 1, alors l'équation diophantienne \(65x - 16y = 5\) admet au moins une solution dans \(\mathbb{Z} \times \mathbb{Z}\).
2. Déterminons l'ensemble (E) des points de (D) à coordonnées entières.
(E) est l'ensemble des points dont les coordonnées sont les solutions de l'équation \(65x - 16y = 5\) dans \(\mathbb{Z} \times \mathbb{Z}\)
(5 ; 20) est une solution particulière de l'équation \(65x - 16y = 5\) et par conséquent\(65\left( {x - 5} \right) = \) \(16\left( {y - 20} \right)\). D'après le théorème de Gauss. il existe \(k \in \mathbb{Z}\) tel que \(x = 16k + 5\) et \(y = 65k + 20\). Donc \(\left( E \right) = \{ M(16k\) \( + 5;65k + 20),\) \(k \in \mathbb{Z}\} \) 0,75 pt
3. Déterminons les points de (D) dont les coordonnées sont des entiers compris entre -126 et 134.
Il s'agit des points M(x ;y) tels que \(x = 16k + 5\) et \(y = 65k + 20\) avec \( - 126 \le y \le 134\).
De \( - 126 \le y \le 134\), on a \(k \in \{ - 2;\) \( - 1;0;1\} \) et par conséquent, ces points ont pour
coordonnées (\(\left( { - 27; - 110} \right)\), \(\left( { - 11; - 45} \right)\), \(\left( { 5; 20} \right)\), et \(\left( { 21; 85} \right)\). 0,5 pt
II.1 Déterminons une équation du plan (P) contenant le point A et de vecteur normal \(\overrightarrow n \).
Soit M(x; y: z) un point de l'espace \(\varepsilon \).
\(M \in (P)\) de vecteur normal \(\overrightarrow n \left( \begin{array}{l}1\\ - 2\\3\end{array} \right)\) équivaut à \(x - 2y + \) \(3z + d = 0\). où \( d \) est un réel.
Par ailleurs \(A\left( \begin{array}{l} - 2\\1\\1\end{array} \right) \in P\) équivaut à \( - 2 - 2 + \) \(3 + d = 0\). d'où d = 1. Donc \(x - 2y + \) \(3z + 1 = 0\) est une équation du plan (P). 0,5 pt
Donnons une expression analytique de la réflexion de plan (P).
Soient M(x; y; z) et M‘(x’; y’; z‘) deux points de l’espace \(\varepsilon \).
M’ est l'image de M par cette réflexion : \(\left\{ \begin{array}{l}\overrightarrow {MM'} = \alpha .\overrightarrow n \\milieu\left[ {MM'} \right] \in \left( P \right)\end{array} \right.\) avec \(\alpha \in \mathbb{R}\)
\(\left\{ \begin{array}{l}x' = \alpha + x\\y' = - 2\alpha + y\\z' = 3\alpha + z\end{array} \right.\) avec \(\alpha \in \mathbb{R}\)
\(\frac{{x + x'}}{2} - \) \(2\frac{{y + y'}}{2} + \) \(3 \times \frac{{z + z'}}{2} = 0\)
Ainsi \(\alpha = - \frac{1}{7}x\) \( + \frac{2}{7}y - \frac{3}{7}z\) \( - \frac{1}{7}\) 1 pt
\(x' = \frac{6}{7}x + \) \(\frac{2}{7}y - \frac{3}{7}z\) \( - \frac{1}{7}\), \(y' = \frac{2}{7}x + \) \(\frac{3}{7}y + \frac{6}{7}z + \frac{2}{7}\) et \(z' = - \frac{3}{7}x + \) \(\frac{6}{7}y - \frac{2}{7}z - \frac{3}{7}\) est l'expression analytique de cette réflexion.
III.1 Déterminons la nature et les éléments caractéristiques de \(g\). 1 pt
Nature : \(g\) est une similitude directe.
Éléments caractéristiques :
• Centre : c'est le point d’affixe \(w = \frac{{ - 2}}{{ - 1 + i}}\) \( = 1 + i\), Donc le point \(\Omega \) est le centre.
• Rapport : \(k = \left| {\frac{{1 + i}}{2}} \right|\) \( = \frac{{\sqrt 2 }}{2}\)
• Angle: \(\theta = Arg\left( {\frac{{1 + i}}{2}} \right)\) \( = \frac{\pi }{4}\)
a) Montrons que pour tout entier naturel \(n\), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés.
Soit \(n\), un entier naturel.
1ere méthode :
\(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) = \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 1}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 2}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 3}}} }} \right) + \) \(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) \)
\(Mes\left( {\widehat {\overrightarrow {\Omega {A_n}} ,\overrightarrow {\Omega {A_{n + 4}}} }} \right) = \) \(4 \times \frac{\pi }{4} = \pi \) ainsi \), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés.
2e méthode :
De proche en proche, on établit que \({Z_{n + 4}} = - \frac{1}{4}{Z_n}\). Ainsi \({A_{n + 4}}\) est l’image de \({A_{n }}\) l‘homothétie de rapport \( - \frac{1}{4}\) et de centre \(\Omega \). Ainsi \), les points \(\Omega \), \(A_n\) et \({A_{n + 4}}\) sont alignés. 0,5 pt
b) Montrons que pour tout entier naturel \(n\). le triangle \(\Omega {A_n}{A_{n + 4}}\)est rectangle et isocèle.
Soit n un entier naturel.
\(\frac{{{Z_{n + 1}} - {Z_n}}}{{{Z_{n + 1}} - {Z_\Omega }}} = \) \(\frac{{1 + \frac{{1 + i}}{2}{Z_n} - {Z_n}}}{{1 + \frac{{1 + i}}{2}{Z_n} - 1 - i}}\) \( = i\), Donc le triangle \(\Omega {A_n}{A_{n + 1}}\) est rectangle et isocèle en \({A_{n + 1}}\) 1 pt

Exercice 2 : 5,25 points (C et E)

Déterminons la loi de probabilité de \(\lambda \).
L’univers image \(\lambda \left( \Omega \right) = \{ 0;\sqrt 3 ;\) \( - \sqrt 3 ;2\sqrt 3 \} \)

2. Calculons de l’espérance mathématique et l'écart type de \(\lambda \).
L'espérance est : \(E\left( \lambda \right) = \) \(\sum {kP\left( {\lambda = k} \right)} \) \( = \) \(\frac{{6\sqrt 3 - 2\sqrt 3 + 6\sqrt 3 }}{{15}}\) \( = \frac{{2\sqrt 3 }}{{15}}\)
La variance est: \(V\left( \lambda \right) = \) \(\sum {{k^2}P\left( {\lambda = k} \right)} \) \( - {E^2}\left( \lambda \right)\) \( = \frac{8}{3}\)
II.1. Déterminons la nature et les éléments caractéristiques de \(\left( \Sigma \right)\).
Nature : \(\left( \Sigma \right)\) est une hyperbole.
Éléments caractéristiques : dans le repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\). 1 pt
• Centre : le point O.
• Sommets : \(B\left( {0;2} \right)\) et \(B'\left( {0; - 2} \right)\).
• Foyers : \(F\left( {0;\sqrt 5 } \right)\) et \(F'\left( {0; - \sqrt 5 } \right)\),
• Directrices: \(\left( \Delta \right)\) : \(Y = \frac{{4\sqrt 5 }}{5}\) et \(\left( {\Delta '} \right)\) : \(Y = - \frac{{4\sqrt 5 }}{5}\).
• Excentricité : \(e = \frac{{\sqrt 5 }}{2}\)
2. a) Donnons l'expression analytique de \(r\). 0,75 pt
Soient \(M\left( {X;Y} \right)\) et \(M'\left( {X';Y'} \right)\) deux points d'armes respectives \(z\) et \(z'\).
\(M' = r\left( M \right)\) \( \Leftrightarrow z = {e^{ - \frac{\pi }{6}i}}z \Leftrightarrow \) \(X' + iY' = \) \(\left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}i} \right)\) \(\left( {X + iY} \right)\)
Ainsi \(X' = \frac{{\sqrt 3 }}{2}X\) \( + \frac{1}{2}Y\) et \(Y' = - \frac{1}{2} + \) \(\frac{{\sqrt 3 }}{2}Y\). qui est l'expression analytique de la rotation \(r\). 0,75 pt
b) Déterminons une équation de l'ensemble \(\left( {\Sigma '} \right)\) image de \(\left( {\Sigma '} \right)\) par \(r\).
Soient M(X ; Y) et M(X’; Y’) deux points d'affixes respectives \(z\) et \(z’\).
\(X' = \frac{{\sqrt 3 }}{2}X\) \( + \frac{1}{2}Y\) et \(Y' = - \frac{1}{2}X + \) \(\frac{{\sqrt 3 }}{2}Y\) ainsi \(X = \frac{{\sqrt 3 }}{2}X'\) \( - \frac{1}{2}Y'\) et \(Y = - \frac{1}{2}X'\) \( + \frac{{\sqrt 3 }}{2}Y'\)
\(4{X^2} - {Y^2} = \) \( - 4 \Rightarrow 4\) \({\left( {\frac{{\sqrt 3 }}{2}X' - \frac{1}{2}Y'} \right)^2} - \) \(\left( { - \frac{1}{2}X' + \frac{{\sqrt 3 }}{2}Y'} \right)\) \( = - 4\)
\(11X{'^2} + Y{'^2}\) \( - 10\sqrt 3 X'Y' + \) \(16 = 0\) (1)
Donc, une équation de l'ensemble \(\left( {\Sigma '} \right)\) image de \(\left( {\Sigma } \right)\) par r est (1) 0,5 pt
c) Déterminons la nature et les éléments caractéristiques de \(\left( {\Sigma '} \right)\). 1 pt
• Nature : \(\left( {\Sigma '} \right)\) est une hyperbole.
• Éléments caractéristiques : dans le repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\)
• Centre : le point O.
• Sommets : \(S(1;\sqrt 3 )\) et \(S'( - 1; - \sqrt 3 )\).
• Foyers : \(r(F)\) et \(r(F’)\).
• Directrices : \(r(\Delta )\) et \(r(\Delta ')\).
• Excentricité : \(e = \frac{{\sqrt 5 }}{2}\)
d) Construisons dans le même repère \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), \(\left( \Sigma \right)\) et\(\left( {\Sigma '} \right)\). 0,5 pt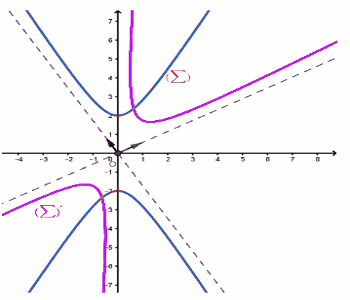

Exercice 3 : 3,25 points (C) / 4,75 points (E)

1. a) Étudions les variations de \(f\).
La fonction \(f\) est dérivable sur \(\mathbb{R}\) et pour tout \(x \in \mathbb{R}\), \(f'(x) = \) \(\frac{{\left( { - x - 1} \right){e^x}}}{{{e^{2x}}}}\) \( = \frac{{\left( { - x - 1} \right)}}{{{e^x}}}\)
Ainsi, \(f\) est strictement décroissante sur \(\left] { - 1; + \infty } \right[\) et strictement croissante sur \(\left] { - \infty ; - 1} \right[\). 0,75 pt
b) Déterminons une équation cartésienne de la tangente \(\left( T \right)\) en \(\left( C \right)\) au point d'abscisse \({ - 1}\).
\(\left( T \right):y = \) \(f'( - 1)(x + 1)\) \( + f( - 1)\). Donc une équation de \(\left( T \right)\) est \(y = e\)
c) Construisons la courbe \(\left( C \right)\) de \(f\) et \(\left( T \right)\) dans le même repère. 1 pt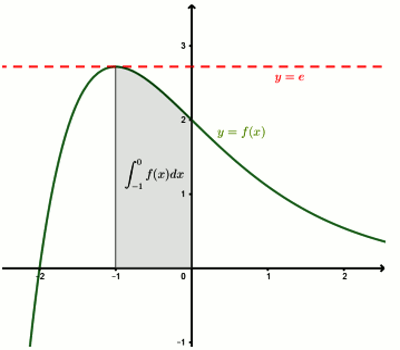
2. a) Déterminons les constantes réelles \(a\), \(b\) et \(c\) telles que la fonction \(F\) définie sur \(\mathbb{R}\) soit une primitive de \(f\).
\(F\) est une primitive de \(F\) sur \(\mathbb{R}\) si et seulement si \(F\) est dérivable sur \(\mathbb{R}\) et pour tout \(x \in \mathbb{R}\),
\(F'(x) = f(x)\), ainsi, pour tout \(x \in \mathbb{R}\), \(\frac{{ - ax + a - b + c{e^x}}}{{{e^x}}}\) \( = \frac{{x + 2}}{{{e^x}}}\) donc \(\left\{ \begin{array}{l}a = - 1\\b = - 3\\c = 0\end{array} \right.\) 0,75 pt
b) Calculons \(\int_{ - 1}^0 {f(x)dx} \).
\(\int_{ - 1}^0 {f(x)dx} = \) \(\left[ {\frac{{ - x - 3}}{{{e^x}}}} \right]_{ - 1}^0\) \( = - 3 + 2e\)
\(\int_{ - 1}^0 {f(x)dx} \) \( = - 3 + 2e\). 0,5 pt

3. (Série E exclusivement)

a) Résolvons \(\left( E \right)\).
l'équation caractéristique de \(\left( E \right)\) est \({r^2} - 2r\) \( + 1 = 0\) qui a pour solution \(r = 1\). Donc les solutions de l'équation \(\left( E \right)\) sont les fonctions U telles que pour tout \(x \in \mathbb{R}\),
\(U(x) = \) \(\left( {Ax + B} \right){e^x}\) avec A et B qui sont des constantes réelles par rapport à \(x\). 0,75 pt
b) Déterminons la solution de \(\left( E \right)\) dont la courbe passe par le point \(A\left( {0;1} \right)\) et admet en ce point une tangente de coefficient directeur 1.
Désignons par \(\left( G \right)\) cette solution. Alors \(G(0) = - 1\) et \(G'(0) = 1\) d'où \(B = - 1\) et \(A + B = 1\), donc \(G(x) = \) \(\left( {2x - 1} \right){e^x}\)

Partie B : Évaluation des compétences (5 points)

Références et solutions
Tâche 1 : Déterminons le coût de ce terrain entier que ABBA souhaite vendre.
Calculons en m2 l'aire \({A_1}\) de ce terrain entier
\({A_1} = \) \(\left( {\int_0^4 {\frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}dx} } \right)\) \( \times 1000 = \) \(\left[ {\ln \left( {{e^x} + {e^{ - x}}} \right)} \right]_0^4\) \( \times 1000 = \) \(\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right)\) \( \times 1000 \approx \) \(3307,188\)
Donc \({A_1} = 3307,188\) m²
Calculons le coût de ce terrain entier.
\(\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right)\) \( \times 2000000\) \( \approx 6614376\) F
Tâche 2 : Déterminons le montant qu'aura ABBA s'il ne souhaite vendre que la portion réservée aux pastèques.
Calculons en m2 l'aire \({A_2}\) de la portion réservée aux pastèques.
\({A_2} = \) \(\left( {\int_0^4 {\left( {\frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} - \frac{1}{4}x} \right)} } \right)\) \( \times 10000 \approx \) \(1307,488\) m²
Calculons le montant pour cette portion réservée aux pastèques.
\(\left( {\ln \left( {\frac{{{e^4} + {e^{ - 4}}}}{2}} \right) - 2} \right)\) \( \times 2000000 \approx \) \(2614376\)
Tâche 3 : Aidons ABBA à retrouver le nombre de sacs de chaque type des deux produits cultivés.
Effectuons le choix des inconnues et procédons à la mise en équations.
Désignons par x et y les nombres de sacs de pastèques et de carottes respectivement.
Nombre total de sacs : \(x + y = 17\)
A la fin de la vente : \(6800\left( {x - 1} \right)\) \( - 3000\left( {y - 1} \right)\) \( = 4000\)
Résolvons le système obtenu nous permet d’avoir : \(\left\{ \begin{array}{l}x = 6\\y = 11\end{array} \right.\)
Donc 6 sacs de pastèques et 11 sacs de carottes.
NB : Le nombre 17 n'étant pas visible sur l'épreuve (confondu à 47) d'une part et l’expression « différence entre…. » d'autre part, accepter aussi l'un des systèmes ci-après :
\(x + y = 17\) et \( - 6800\left( {x - 1} \right)\) \( + 3000\left( {y - 1} \right)\) \( = 4000\) soit
\(\left\{ \begin{array}{l}x + y = 17\\ - 34x + 15y = 1\end{array} \right.\)
Ou \(x + y = 47\) et \(6800\left( {x - 1} \right) - \) \(3000\left( {y - 1} \right)\) \( = 4000\) soit \(\left\{ \begin{array}{l}x + y = 47\\34x - 15y = 39\end{array} \right.\)
Ou \(x + y = 47\) et \( - 6800\left( {x - 1} \right)\) \( + 3000\left( {y - 1} \right)\) \( = 4000\) soit \(\left\{ \begin{array}{l}x + y = 47\\ - 34x + 15y = 1\end{array} \right.\)
Et ces trois derniers systèmes ont respectivement pour couples solutions \(\left( {\frac{{254}}{{49}};\frac{{579}}{{49}}} \right)\) , \(\left( {\frac{{744}}{{49}};\frac{{1559}}{{49}}} \right)\) ou \(\left( {\frac{{704}}{{49}};\frac{{1599}}{{49}}} \right)\) et dans ces trois derniers cas, le problème posé n'a pas de solution.