Partie A : Évaluation des ressources 15 points
I Exercice 1 : 3 points
1. Déterminons le nombre total de fonctions f que l’on peut former.
Former une fonction, c'est faire une 2-liste de l'ensemble \(\{ - \frac{{17}}{3}; - 2;\) \( - 1;0;1;2\} \). Il y a donc au total \({6^2} = 36\) fonctions possibles ; soit 36 fonctions au total. 1 pt
2. Déterminons le nombre de telles fonctions f qui sont des fonctions homographiques.
Former une fonction homographique, c'est former une fonction f avec \(\alpha = 0\). C'est donc obtenir les 2-listes (0;b) avec b appartenant à \(\{ - \frac{{17}}{3}; - 2;\) \( - 1;0;1;2\}\). Il y a donc au total 6 fonctions homographiques possibles. 1 pt
3.3) Déterminons l’ensemble de définition de f.
Soit \(x \in R\), f(x) existe si et seulement si \(2x - 3 \ne 0\); c’est-à-dire pour \(x \ne \frac{3}{2}\) L'ensemble de définition de f est donc \(D = R\backslash \left\{ {\frac{3}{2}} \right\}\) 0,25 pt
b) Déterminons le couple \(\left( {a,b} \right)\) pour lequel \(f(x) = x - \frac{4}{3}\) pour \(x \ne \frac{3}{2}\)
Soit \(x \ne \frac{3}{2}\) ainsi \(f(x) = \) \(x - \frac{4}{3}\) \( \Rightarrow f(x) = \) \(\frac{{\left( {2x - 3} \right)\left( {x - \frac{4}{3}} \right)}}{{2x - 3}}\) après développement du numérateur et identification des coefficients, nous obtenons
\(\left( {a;b} \right) = \) \(\left( {3; - \frac{{17}}{2}} \right)\) 0,75 pt
Exercice 2 : 3,5 points
1. Déterminons l'image du triangle ABC par la symétrie orthogonale d'axe (OI).
On a \({S_{\left( {OI} \right)}}(A) = B\), \({S_{\left( {OI} \right)}}(B) = A\), \({S_{\left( {OI} \right)}}(C) = D\)
L'image du triangle ABC par la symétrie orthogonale d'axe (OI) est donc le triangle ABD. 0,5 pt
2. Montrons que le point F est le centre de gravité du triangle ABC.
(OB) et (IC) sont des médianes du triangle ABC et F est leur point de rencontre. Le point F est donc le centre de gravité du triangle ABC. 0,5 pt
3. Déduisons-en que E est le centre de gravité du triangle ABD.
ABD et E sont les images respectives de ABC et F par \({S_{\left( {OI} \right)}}\), Or F est le centre de gravité de ABC et \({S_{\left( {OI} \right)}}\) conserve le barycentre ; donc E est le centre-de gravite de ABD. 0,5 pt
4.a) Montrons que (EF) et (AB) sont parallèles.
On a \(\overrightarrow {OE} = \frac{1}{3}\overrightarrow {OA} \) et \(\overrightarrow {OF} = \frac{1}{3}\overrightarrow {OB} \) car E et F sont respectivement les centre de gravité des triangles ABD et ABC. D'où \(\overrightarrow {AB} = \overrightarrow {OB} \) \( - \overrightarrow {OA} = 3\overrightarrow {OF} \) \( - 3\overrightarrow {OE} = \) \(3(\overrightarrow {OF} - \overrightarrow {EO} )\) \( = 3\overrightarrow {EF} \)
(EF) et (AB) sont donc parallèles. 0,5 pt
b) Déterminons \(h(B) = F\). 0,5 pt
L’homothétie h transforme A en E et donc la droite (AB) en la droite passant par E et parallèle à (AB), c’est-à-dire en (EF). Comme \(B \in \left( {AB} \right)\), alors \(h(B) \in \left( {EF} \right)\)
0, B et h(B) étant alignés, alors h(B) est sur (EF) et (OB). Donc \(h(B) = F\)
5. Déterminons- l'ensemble des points M du plan tels que :
\(||2\overrightarrow {MA} + 3\overrightarrow {MB} \) \( + \overrightarrow {MC} || = ||\overrightarrow {NA} \) \( - \overrightarrow {NB} ||\)
Soit M un point du plan,
\(||2\overrightarrow {MA} + 3\overrightarrow {MB} \) \( + \overrightarrow {MC} || = ||\overrightarrow {NA} \) \( - \overrightarrow {NB} ||\) \( \Leftrightarrow ||6\overrightarrow {MK} || = \) \( ||\overrightarrow {BA} ||\), soit \(KM = \frac{1}{6}AB\)
L'ensemble des points M du plan tels que \(||2\overrightarrow {MA} + 3\overrightarrow {MB} \) \( + \overrightarrow {MC} || = ||\overrightarrow {NA} \) \( - \overrightarrow {NB} ||\) est le cercle de centre K et de rayon \(\frac{1}{6}AB\). 1 pt
Exercice 3 / 4 points
1.a} Montrons que \(\left( {{Q_n}} \right)\) est une suite géométrique et précisons son premier terme et sa raison. 1 pt
On a \({Q_{n + 1}} = {P_{n + 1}} + \) \(5000 = 1,1{P_n}\) \( + 5500 = 1,1\) \(({P_n} + 5000)\) \( = 1,1{Q_n}\) donc \(\left( {{Q_n}} \right)\) est une suite géométrique de raison 1,1. et de premier \({Q_0} = {P_0} + \) \(5000 = 10000\)
b) Exprimons \({{Q_n}}\) en fonction de n puis déduisons que \({P_n} = 10000 \times \) \({\left( {1,1} \right)^n} - 5000\)
On a \({Q_n} = 10000{\left( {1,1} \right)^n}\), D’ou \({P_n} = 10000 \times {\left( {1,1} \right)^n}\) \( - 5000\)
2. Déterminons le nombre de poissons que comptera cette réserve le 1er Janvier2030.
Soit \({x_n}\) le nombre de poissons dans cette réserve le 1er Janvier de l'année 2015 + n.
On a : \({x_0} = 5000\) et \({x_{n + 1}} = {x_n}\) \( + \frac{{10}}{{100}}{x_n}\) \( + 500 = \) \(\left( {1,1} \right){x_n}\) \( + 500\). 1.a) et 1.b) donne alors \({x_n} = 10000\) \(\left( {1,1} \right){x_n} - 5000\), Or le 1er Janvier 2030 le nombre de poissons dans cette réserve sera \({x_{15}} = \) \(10000{\left( {1,1} \right)^{15}}\) \( - 5000 \approx \) \(36772\)
Il y aura alors (environ) 36772 poissons dans cette réserve au 1er Janvier 2030. 2 pts
Exercice 4 / 4,5 points
1.a) Démontrons que le point \(\Omega \left( {\frac{3}{2};2} \right)\) est un centre de symétrie de \({C_f}\)
Pour \(\frac{3}{2} + x \in \) \(\left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \left] {\frac{3}{2}; + \infty } \right[\) , appartient aussi à \(\frac{3}{2} - x \in \) \(\left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \left] {\frac{3}{2}; + \infty } \right[\)
Et \(f\left( {\frac{3}{2} - x} \right) + \) \(f\left( {\frac{3}{2} + x} \right)\) \( = 2 \times 2\)
Donc le point \(\left( {\frac{3}{2};2} \right)\) est un centre de symétrie de \({C_f}\). 0,5 pt
b) Déterminons la limite de f à droite de \({\frac{3}{2}}\) et la limite de f en \( + \infty \). 0,5 pt
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{3}{2}} \right)}^ + }} f(x)\) \( = + \infty \) et \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) \( = + \infty \)
c) Démontrons que la droite \(\Delta :y = x + \frac{1}{2}\) est asymptote à \({C_f}\) en \( + \infty \); et justifions que la droite \(\Delta ':x = \frac{3}{2}\) est asymptote à \({C_f}\)
2.a) Déterminons l’expression f’(x) de la dérivée de f 0,5 pt
Pour tout \(x \in \left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \left] {\frac{3}{2}; + \infty } \right[\), nous avons \(f'(x) = \) \(\frac{{4{x^2} - 12x - 2}}{{{{\left( {2x - 3} \right)}^2}}}\)
b) Étudions le signe de f’(x) 0,5 pt
Étudions le signe de f’(x) pour \(x \in \left] {\frac{3}{2}; + \infty } \right[\)
\(f'(x) = 1 - \) \(\frac{{11}}{{{{\left( {2x - 3} \right)}^2}}}\)
• Pour \(x \in \) \(\left] {\frac{{3 + \sqrt {11} }}{2}; + \infty } \right[\), \(f'(x) \succ 0\)
• Pour \(x \in \) \(\left] {3;\frac{{3 + \sqrt {11} }}{2}} \right[\), \(f'(x) \prec 0\)
c) Dressons le tableau des variations de f sur \(\left] {\frac{3}{2}; + \infty } \right[\) 0,75 pt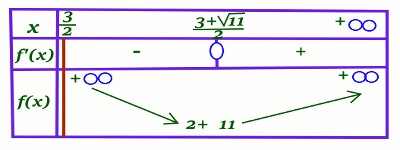 d) Construisons \({C_f}\) sur \(\left] {\frac{3}{2}; + \infty } \right[\), puis complétons-la sur \(x \in \left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \left] {\frac{3}{2}; + \infty } \right[\) 1 pt
d) Construisons \({C_f}\) sur \(\left] {\frac{3}{2}; + \infty } \right[\), puis complétons-la sur \(x \in \left] { - \infty ;\frac{3}{2}} \right[\) \( \cup \left] {\frac{3}{2}; + \infty } \right[\) 1 pt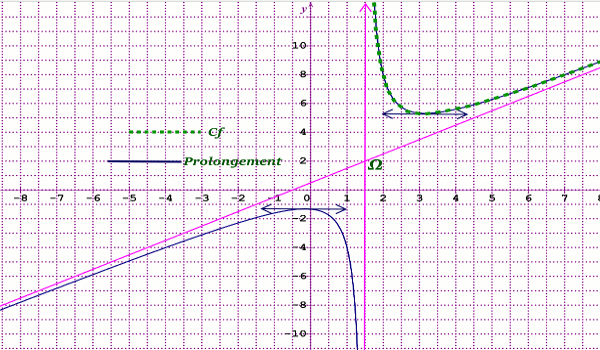 Partie B : Évaluation des compétences
Partie B : Évaluation des compétences
1. Déterminons combien il lui faut pour acheter la quantité utile de fil barbelé.
Déterminons les dimensions de ce parc.
Soient x et y les dimensions (en m) des côtes perpendiculaires de ce parc. On a \(\frac{{xy}}{2} = 750\) et \({x^2} + {y^2}\) \( = {65^2}\)
Ainsi : \({\left( {{x^2} + {y^2}} \right)^2}\) \( = {x^2} + {y^2}\) \( + 2xy = \) \({65^2} + 4 \times \) \(750\) ce qui donne le système suivant \(\left\{ \begin{array}{l}xy = 1500\\x + y = 85\end{array} \right.\)
Si x = 25, alors y = 60. Si x = 60, alors y = 25. Donc les dimensions des côtés perpendiculaires de ce parc sont 60 m et 25 m. 0,5 pt
• Déterminons la longueur utile de fil barbelé. 0,5 pt
En mètres, cette longueur est 3(25 + 60 + 6S) = 450.
• Déterminons le coût de la quantité utile de fil barbelé. 0,5 pt
Les 450 mètres de fil barbelé nécessaire coûtent en FCFA) 450 x 1250 = 562500.
2. Déterminons le nombre d'animaux de chaque espèce dans ce parc.
• Déterminons les nombres de pattes, de têtes et de cornes de chaque espèce d'animaux dans ce parc. 0,5 pt
Un rhinocéros a 4 pattes, une tête et une corne ;
Un taureau a 4 pattes, une tête et 2 cornes ;
Une oie a 2 pattes, une tête et 0 corne. "
Traduisons en langage mathématiques, les informations sur les espèces dans ce parc. 0,5 pt
Soient x, y et z les nombres respectifs de rhinocéros, de taureaux et d'oies dans ce parc, on a :
\(4x + 4y + \) \(2z = 300\), \(x + y + z\) \( = 100\) et \(x + 2y\) \( = 65\)
• Résolvons le système ainsi obtenu, on obtiendra x = 35, y = 15 et z = 50
Il y a donc dans ce parc. 35 rhinocéros. 15 taureaux et 50 oies. 0,5 pt
3. Déterminons l’âge qui correspond à la dose de vaccin que recevra chaque oie.
• Déterminons l’effectif cumulé croissant de chaque tranche d'âge. 0,5 pt
| Ages en années | [ 0 ; 1 [ | [ 1 ; 2[ | [ 2 ; 3 [ | [ 3 ; 4 [ | [ 4 ; 5 [ | Total |
| Effectifs | 12 | 11 | 4 | 13 | 10 | 50 |
| E C C | 12 | 23 | 27 | 40 | 50 |
Déterminons l‘âge médian des oies de ce parc. 0,5 pt
La médiane Me appartient à la tranche d'âge [2 ; 3[.
Par interpolation linéaire, on a : \(\frac{{27 - 25}}{{27 - 23}} = \) \(\frac{{2 - Me}}{{3 - 2}}\) \( \Rightarrow Me = 2,5\)
D'où Me = 2,5
L'âge qui correspond à la dose de vaccin que recevra chaque oie de ce parc est de deux ans et demi. 0,5 pt

