Cette épreuve étalée sur deux pages, est constituée de deux parties indépendantes.
Partie A : Évaluation des ressources (15 points)
Exercice I : (4 points)
L'unité des longueurs est le centimètre.
ABCD est un rectangle de centre O, de dimension AB = 6 et BC = 8. '
G est 1e centre de gravité du triangle ABC et I le milieu de [AB].
1) Faire une figure. (1 pt)
2) Soit h une application du plan dans lui-même transformant chaque point M en un point M' tel que \(\overrightarrow {MM'} = \overrightarrow {MA} + \) \(\overrightarrow {MB} + \overrightarrow {MC} \)
a) Démontrer que h est une homothétie de centre G et de rapport -2. (0,75 pt).
b) Quelle est l'image du point B par l’homothétie h ? (0,5 pt)
3) Soit (\(\sum \)) le lieu des points M du plan tels que \(M{A^2} - M{B^2}\) \( = 36\)
a) Démontrer que le point C appartient à (\(\sum \)). (0,5pt)
b) Démontrer que (\(\sum \)) est une droite qu'on déterminera et qu'on représentera. (0,75 pt)
c) Déterminer et représenter l'image (\(\sum '\)) de (\(\sum \)) par l'homothétie h. (0,5 pt)
Exercice 2 : (5 points)
On considère la fonction numérique f à variable réelle définie par l’expression
\(f(x) = \) \(\frac{{2x + 1}}{{1 - x}}\)
Le plan est rapporté au repère orthonormé \(\left( {0;\overrightarrow i ,\overrightarrow j } \right)\). (Cf) est la courbe de f.
1) a) Justifier que l’ensemble D ; de définition de f est \(] - \infty ;1[ \cup \) \(]1; + \infty [\). Calculer les limites de f aux bornes de cet ensemble. (1.25 pt)
b) Déterminer les équations des deux asymptotes a la courbe (Cf). (0,5 pt)
2) Démontrer que le point \(\Omega \left( \begin{array}{l}1\\ - 2 \end{array} \right)\) est un centre de symétrie a la courbe (Cf). (0,5 pt)
3) Déterminer pour \(x \ne 1\), f’(x) et dresser le tableau de variation de f. (1 pt)
4) Tracer avec soin la courbe (Cf). On placera le point d’intersection de (Cf) avec l’axe des abscisses. (1,25 pt)
5) On pose pour x appartenant à Df, \(g(x) = \) \(\frac{{\left| {2x + 1} \right|}}{{1 - x}}\) représenter la courbe (Cg) de g. (0.5 pt)
Exercice 2 : (3 points)
Une suite (Un) vérifie l’égalité \({U_{n + 1}} = 2{U_n}\) \( - 2n + 1\) pour n appartenant à N, avec \({U_0} = 1\).
1) Calculer \({U_{1}}\), \({U_{2}}\), \({U_{3}}\) et conjecturer la valeur de \({U_{100}}\). (1,25 pt)
2) Soit k appartenant à N. 0,75 pt
Démontrer que si \({U_k} = 2k + 1\), alors on a \({U_{k + 1}} = \) \(2\left( {k + 1} \right) + 1\)
3) On admet que \(\left( {{U_n}} \right)\) est une suite arithmétique _
Calculer la somme \({U_0} + {U_1} + \) \({U_2} + ... + {U_n}\) en fonction de n uniquement. (1 pt)
Exercice 3 : (3 points)
Un mois après le déclenchement de l’épidémie de COVID-19, un pays a dressé le tableau statistique des personnes infectées suivant des tranches d'âges (en années) dans le tableau statistique suivant :
| Tranches d'âges (en années) | [0; 15[ | [15; 20[ | [20; 40[ | [40; 60[ | [60; 80[ |
| Effectifs des individus touchés | 12 | 16 | 60 | 48 | 16 |
1) Déterminer l’âge moyen des individus touchés par cette épidémie. (0,5.pt)
2) Construire la courbe des effectifs cumulés croissants aussi appelé polygone des effectifs ci mes croissants. (1,5 pt)
3) Déterminer l’âge médian des personnes infectées au sein de la population. (0,5 pt)
4) Un groupe de deux individus avait été choisi parmi les individus de la tranche d'âges [20 ; 40[ pour un traitement expérimental. De combien de façons pouvait-on effectuer un tel choix? (0,5 pt)
Partie B : Évaluation des compétences (5 points)
Situation :
ABOU habite la localité d'Edéa en bordure du fleuve Sanaga. Il a une vieillie pirogue à moteur qui lui permet de se déplacer sur la Sanaga. Afin de ménager son moteur ou sa vieille boite de vitesse, il se déplace chaque fois à vitesse constante pour tout déplacement de plus de 5 km à bord de cette pirogue. Pour un déplacement à vitesse constante v et pendant chaque heure, la consommation de carburant en titres de cette pirogue \(0,4 + 0,001{v^2}\) .
Dans le village riverain de la Sanaga et situé à 40 km d'Edéa par voie fluviale.
ABOU avait acheté un champ. Il voulait sécuriser ce champ en l’entourant de grillage. A bord de sa pirogue et à vitesse constante v, ABOU et son fils ABDEL s’étaient rendus dans ce champ afin de déterminer la longueur du grillage nécessaire pour cette sécurisation. Arrivé au champ, ABDEL a constaté que le champ a Ia forme d'un triangle
ABC avec AB = 300m et AC = 400 m.
N'ayant pas eu du temps pour mesurer le coté [BC], ABDEL a mesuré l’angle en A de ce triangle tout en promettant à son père perplexe, la valeur exacte de BC une fois de retour à Edéa. (Voir figure ci-dessous).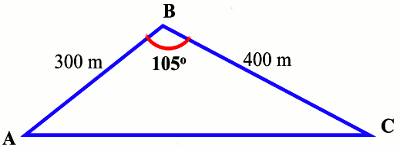 Pour le retour mur à Edéa, ABDEL a demandé à son père de diminuer sa vitesse de l‘aller de 5 km /h et cette diminution leur a permis de réduire la consommation de carburant de l'aller de 4 cl.
Pour le retour mur à Edéa, ABDEL a demandé à son père de diminuer sa vitesse de l‘aller de 5 km /h et cette diminution leur a permis de réduire la consommation de carburant de l'aller de 4 cl.
Tâches
1) Déterminer la vitesse qu'ABOU aurait dû adopter d'Edéa au champ, pour avoir une consommation minimale de carburant à l'aller. (1,5 pt)
2) Déterminer la vitesse de la pirogue qu'avait adopté ABOU à l’aller. (1,5 pt)
3) Déterminer en mètres, la longueur exacte du grillage nécessaire pour entourer complétement le champ. (1,5 pt)
Présentation : (0,5 pt)


