Exercice I : 4 points
1. Soit n un entier naturel, \(n \ge k\)
a) Exprimons un en fonction de n, uk et r 0,75 pt
(un) étant une suite arithmétique de raison r, \({u_n} = \) \({u_k} + \) \((n - k)r\)
b) Exprimons \({S_n} = \) \({u_k} + \) \({u_{k + 1}} + \) \(... + {u_n}\) 0,75 pt
Ainsi :
\({S_n} = \) \(\frac{{n - k + 1}}{2}\) \(({u_k} + {u_n})\) \( = \frac{{n - k + 1}}{2}\) \((2{u_k} + \) \((n - k)r)\)
2.a) Déterminons la raison de cette suite 0,75 pt
Notons u5 et u10 respectivement le 5ieme et le 10ieme termes de cette suite, r sa raison, on :
\({u_{10}} = \) \({u_5} + 5r\) \( \Rightarrow r = \) \(\frac{{{u_{10}} - {u_5}}}{5}\) \( = 2\)
Cette suite est de raison 2
2.b) Déterminons la raison de cette suite si le premier terme est 2 0,75 pt
\(30 = \) \(\frac{{5(2 \times 2 + 4r)}}{2}\)
Cette suite est de raison 2
3.a) Déterminons les nombres de petits-fils de Mme Wedze 0,75 pt
Désignons par \(n \in N\) ce nombre, le plus grand des ainés recevra un nombre de bonbons égal à : \(2 + \) \(2(n + 1)\), soit 2n le nombre de petits-fils qui recevront au total \(\frac{{n(2 + 2n)}}{2}\) \( = n(n + 1)\) qui est par ailleurs égal à 6n, d’après la remarque de l’aîné des petits-fils.
n vérifie la relation \(n(n + 1)\) \( = 6n\), de la résolution de cette équation, on obtient n=0 et n=5.
Conclusion, Mme Wedge a 5 petits-fils.
3.b) Déterminons le nombre de bonbons que comptait le paquet 0,25 pt
\(5 \times 6 = 30\) bonbons.
Exercice II / 5points
1. Traçons dans le repère convenablement choisi, l’histogramme de cette série 1,5 pt
L’aire de chaque rectangle de l’histogramme et proportionnelle à l’effectif de la classe qu’il représente. Par conséquent, les hauteurs des rectangles représentant les classes [145 ;155[ ,[155 ;160[, [160 ;165[, [165 ;170[, et [170 ;190[ sont respectivement proportionnelles à leurs densités. On a donc
\({d_1} = \) \(\frac{5}{{155 - 145}}\) \( = 0,5\)
\({d_2} = \) \(\frac{10}{{160 - 155}}\) \( = 2\)
\({d_3} = \) \(\frac{15}{{165 - 160}}\) \( = 3\)
\({d_4} = \) \(\frac{5}{{170 - 165}}\) \( = 1\)
\({d_5} = \) \(\frac{5}{{190 - 170}}\) \( = 0,25\)
Si a, b, c, d et e désignent les hauteurs respectivement de ces rectangles, alors
\(\frac{a}{{0,5}} = \) \(\frac{b}{2} = \) \(\frac{c}{3} = \) \(\frac{d}{1} = \) \(\frac{e}{{0,25}}\)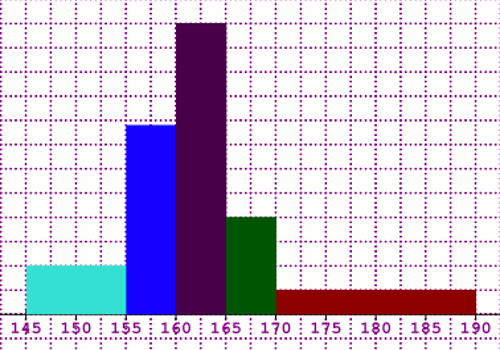 2.a) Traçons le polygone des effectifs cumulés croissants de cette série 1,25 pt
2.a) Traçons le polygone des effectifs cumulés croissants de cette série 1,25 pt
Le tableau des effectifs cumules croissante (E.C.C) est le suivant :
| Taille | [145;155[ | [155;160[ | [160;165[ | [165;170[ | [170;190[ |
| E.C.C | 5 | 15 | 30 | 35 | 40 |
Le polygone des effectifs cumulés croissants est le suivant :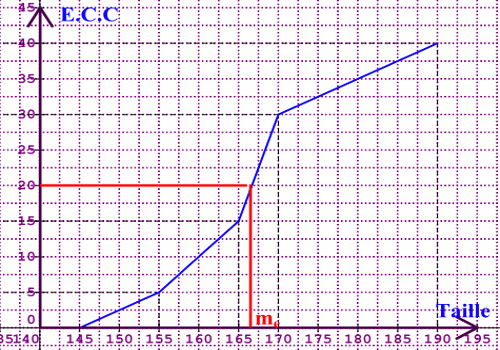 2.b) Déterminons graphiquement et par calcul la médiane me au centimètre prés :
2.b) Déterminons graphiquement et par calcul la médiane me au centimètre prés :
Graphiquement, me est l’abscisse du point de cordonnées 20. Donc \({m_e} \approx 162\) cm
Par calcule, on a \(\frac{{{m_e} - 160}}{{20 - 15}} = \) \(\frac{{165 - 160}}{{30 - 15}}\) ; ainsi, \(me = \) \(160 + \frac{5}{3}\) \({m_e} \approx 162\) cm 1 pt
3. Calculons la moyenne m et la variance v de cette série 1,25 pt
La série des centres est :
| Taille | [145;15[ | [155;160[ | [160;165[ | [165;170[ | [170;190[ |
| Centre | 150 | 157,5 | 162,5 | 167,5 | 180 |
\(m = 162,5\)
\(v = 67,18\)
Problème /11 points
Partie A
1.a) Montrons que pour tout point M du plan, 0,75 pt
\(O{M^2} + \) \(A{M^2} = \) \(2G{M^2} + \) \(\frac{1}{2}O{A^2}\)
Soit M un point du plan, comme G est le milieu de [AO], on a :
\(O{M^2} + \) \(A{M^2} = \) \({(\overrightarrow {OG} + \overrightarrow {GM} )^2}\) \( + (\overrightarrow {AG} + \) \(\overrightarrow {GM} {)^2}\) \( = {(\frac{{\overrightarrow {OA} }}{2})^2} + \) \({(\frac{{\overrightarrow {OA} }}{2})^2} + \) \(2{\overrightarrow {GM} ^2}\)
\( = \frac{{{{\overrightarrow {OA} }^2}}}{2}\) \( + 2{\overrightarrow {GM} ^2}\)
1.b) Déduisons la nature et les éléments caractéristiques de l’ensemble (\({\Gamma _1}\)) des points M du plan tels que : \(O{M^2} + \) \(A{M^2} = \) \(O{A^2}\) 0,75pt
Soit M un point de (\({\Gamma _1}\)), on a
\(O{M^2} + \) \(A{M^2} = \) \(O{A^2} \Leftrightarrow \) \(\frac{{O{A^2}}}{2} + \) \(2G{M^2} = \) \(O{A^2}\)
Soit : \(G{M^2} = \) \(\frac{{O{A^2}}}{4}\) ainsi \(GM = \frac{{OA}}{2}\). (\({\Gamma _1}\)) est un cercle de centre G et de rayon \(\frac{{OA}}{2}\).
2.a) Montrons que l’ensemble (\({\Gamma _2}\)) est un cercle dont on précisera le centre et le rayon r 0,75 pt
Soit M(x,y) un point tel que : \({x^2} + \) \({y^2} - \) \(2x - \) \(4y = 0\), on a : \({(x - 1)^2} + \) \({(y - 2)^2}\) \( = 5\)
Donc (\({\Gamma _2}\)) est un cercle de centre G(1 ;2) et de rayon \(r = \sqrt 5 \)
2.b) Vérifions que A(2 ;4) appartient à (\({\Gamma _2}\)) et donnons une équation de la tangente (T) à (\({\Gamma _2}\)) en ce point 0,75 pt
• \(GA = \sqrt 5 \) donc A(2 ;4) appartient à (\({\Gamma _2}\)). On peut aussi montrer que les coordonnées de A vérifient l’équation de (\({\Gamma _2}\)).
• Un vecteur normal de (T) est \(\overrightarrow {GA} (1;2)\), une équation de (T) est alors \(x + 2y\) \( + c = 0\), c étant un réel. Comme A(2 ;4) appartient à (T), on a \(2 + 2\) \( \times 4 + c\) \( = 0\) et alors, c=-10. Une équation de (T) est donc
\(x + 2y\) \( - 10 = 0\)
2.c) Traçons (\({\Gamma _2}\)) et (T)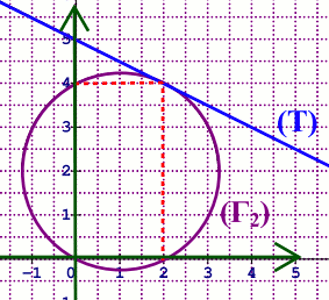
Partie B :
1.a) Calcule les limites de f aux bornes D : \(D = \) \(] - \infty ;1[\)\( \cup ]1; + \infty [\)
• \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) \( = - \infty \) 0,25 pt
• \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) \( = + \infty \) 0,25 pt
• \(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\) \( = - \infty \) 0,25 pt
• \(\mathop {\lim }\limits_{x \to {1^ + }} f(x)\) \( = + \infty \) 0,25 pt
1.b) Équation de l’asymptote à la courbe 0,25 pt
• \(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\) \( = - \infty \)
• \(\mathop {\lim }\limits_{x \to {1^ + }} f(x)\) \( = + \infty \)
Alors, x=1 est asymptote verticale à la courbe (Cf)
1.c Déterminons trois réels a, b et c tels que pour tout x de D on a :
\(f(x) = \) \(ax + b\) \( + \frac{c}{{x - 1}}\) 0,75 pt
Soit \(x \in D\), on a
\(f(x) = \) \(\frac{{{x^2}}}{{x - 1}}\) \( = \) \(\frac{{x(x - 1) + (x - 1) + 1}}{{x - 1}}\) \( = \) \(x + 1 + \) \(\frac{1}{{x - 1}}\)
Alors a=1, b=1 et c=1.
1.d) Montrons que la droite \((\Delta )\) : y=x+1 est une asymptote à la courbe (Cf) : on a
\(\mathop {\lim }\limits_{x \to - \infty } (f(x)\) \( - (x + 1))\) \( = \mathop {\lim }\limits_{x \to + \infty } (f(x)\) \( - (x + 1))\) \( = 0\)
La droite \((\Delta )\) : y=x+1 est une asymptote oblique à la courbe (Cf) 0,25pt
2.a) Déterminons la fonction dérivée et dressons le tableau de variation de la fonction f
\(f'(x) = \) \(\frac{{x(x - 2)}}{{{{(x - 1)}^2}}}\) 0,75 pt
Tableau de variation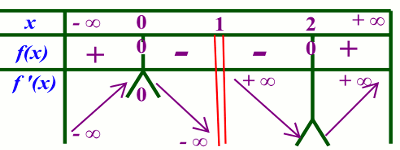 2.b) Montrons si oui ou non, il existe des points de (Cf) où la tangente est parallèle à \((\Delta )\) 0,5 pt
2.b) Montrons si oui ou non, il existe des points de (Cf) où la tangente est parallèle à \((\Delta )\) 0,5 pt
La tangente à (Cf) en un point d’abscisse \(\alpha \ne 1\) est parallèle à \((\Delta )\) si et seulement si \(f'(\alpha ) = 1\). On a ainsi
\(f'(\alpha ) = \) \(\frac{{\alpha (\alpha - 2)}}{{{{(\alpha - 1)}^2}}}\) \( = 1\) soit \({\alpha ^2} - 2\alpha \) \( = {\alpha ^2} - \) \(2\alpha + 1\). Ceci est impossible, il n’existe donc pas de point (Cf) où la tangente est parallèle à \((\Delta )\)
3. Traçons la courbe (Cf)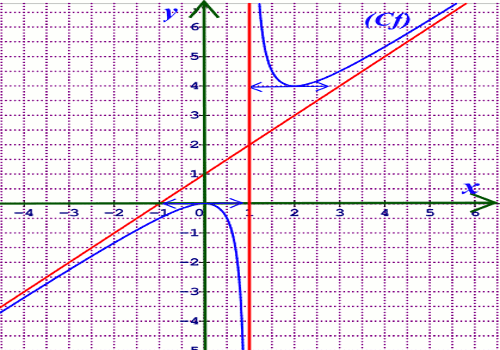 4.a) Calcule de \(\Delta m\) :
4.a) Calcule de \(\Delta m\) :
\(\Delta m = {m^2}\) \( - 4m\) 0,25 pt
Remarque : L’équation (Em) est équivalente à f(x) = m et ainsi, les solutions de (Em) sont les abscisses des éventuels points communs à la courbe de f et de la droite d’équation y=m.
4.b) Déterminons les valeurs de m pour lesquelles (Em) admet une solution unique : 0,5 pt
\(\Delta m = 0\) si et seulement si (m=0 ou m=4)
(Em) admet une solution unique pour m=0 ou m=4.
4.c) Déterminons les valeurs de m pour lesquelles (Em) admet deux solutions (0,5 pt)
(Em) admet deux solutions distinctes si et seulement si \({m^2} - \) \(4m \succ 0\), soit
\(m \in ] - \infty \) \(;0[ \cup ]4;\) \( + \infty [\)
5.a) Exprimons en fonction de m, la somme Sm et le produit Pm de ces solutions 0,5 pt
\(\left\{ \begin{array}{l}{S_m} = m\\{P_m} = m\end{array} \right.\)
5.b) Déterminons m si cela est possible tel que les solutions x1 et x2 soient toutes négatives
X1 et x2 sont toutes negatives si et seulement si \({m^2} - \) \(4m \succ 0\), \({P_m} \succ 0\) et \({S_m} \prec 0\). Soit \(m \succ 4\) et \(m \prec 0\)
Il n’existe donc pas de valeur de m telle x1 et x2 soient toutes négatives
5.c) Déterminons les valeurs de m pour lesquelles les solutions x1 et x2 sont de signes contraires 0,5pt
Les solutions sont de signes contraires si et seulement si (\({m^2} - \) \(4m \succ 0\) et \(m \prec 0\) ) ; soit \(m \in ] - \infty ;0[\). Les solutions x1 et x2 sont de signes contraires pour \(m \in ] - \infty ;0[\)
5.d) Déterminons les valeurs de m pour lesquelles les solutions x1 et x2 sont toutes positives 0,5 pt
Les solutions x1 et x2 sont toutes positives si et seulement si (\({m^2} - \) \(4m \succ 0\) et \(m \succ 0\) ), soit \(m \in ]4; + \infty [\). Les solutions x1 et x2 sont toutes positives pour \(m \in ]4; + \infty [\)

