Exercice I : Energie mécanique 6 pts
1ere méthode : Théorème de l’énergie cinétique
1. Bilan des forces s’exerçant sur le palet 0,5x2=1pt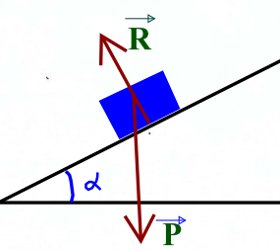
2. Enoncé du théorème de l’énergie cinétique
Dans un référentiel galiléen, la variation de l’énergie cinétique d’un solide entre deux instants donnés est égale à la somme algébrique des travaux de toutes les forces appliquées au solide entre ces deux instants 1 pt
3. Longueur L parcourue par le mobile
Appliquons le TEC au palet entre A et B
\({E_{{C_B}}} - \) \({E_{{C_A}}} = \) \({W_{\overrightarrow {AB} }}(\overrightarrow P ) + \) \({W_{\overrightarrow {AB} }}(\overrightarrow R )\)
\(0 - \frac{1}{2}mV_A^2\) \( = - mgL\sin (\alpha )\) \( + 0\)
\(L = \frac{{V_A^2}}{{2g\sin (\alpha )}}\)
AN : \(L = 1,44\) m
2eme méthode : Conservation de l’énergie mécanique
1. Energie potentielle : C’est l’énergie que possède un système de fait des positions relatives de ses parties en interaction 0,5 pt
2. Energie mécanique du système (Palet-Terre) au point A
\({E_{{m_A}}} = \) \({E_{{C_A}}} + {E_{{P_A}}}\) \( = \frac{1}{2}mV_A^2\)
\({E_{{m_A}}} = 62,5\) J
3. Expression de l’énergie du système (palet-terre) au point B
\({E_{{m_B}}} = \) \({E_{{C_B}}} + {E_{{P_B}}}\)
Or \({E_{{C_B}}} = 0\) et \({E_{{P_B}}} = mg{z_B}\)
Il vient que :
\({E_{{m_B}}} = mg{z_B}\)0,5pt
4. Justifions que l’énergie mécanique se conserve et déduisons la longueur L parcourue par le mobile
Il n’y a pas de frottements : l’énergie mécanique se conserve 0,25 pt
Déduisons la longueur L
L’énergie mécanique se conserve donc :
\({E_{{m_A}}} = {E_{{m_B}}}\)
\(\frac{1}{2}mV_A^2\) \( = mg.{z_B}\)
\(L = \frac{{V_A^2}}{{2g\sin (\alpha )}}\) 0,25pt
\(L = 1,44\) m0,25pt
Exercice 2 : Lentilles et instruments d’optique 7pts
Partie 1 : Lentilles spheriques minces 3,5 pts
1. Calcule du rayon de courbure R
\(C = (n - 1)\) \((\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}})\)
\({R_1} = {R_2}\) \( = R\)
\(R = \frac{{2(n - 1)}}{C}\)
AN : \(R = 0,1\) m
2. Distance focale f de la lentille L2
(L1) et (L2) sont accolées, alors : \(C = {C_1} + {C_2}\) 0,5 pt
\({C_2} = C - {C_1}\) \( = \frac{1}{{{f_2}}}\)
Il vient dont que :
\({f_2} = \frac{1}{{C - {C_1}}}\) 0.5pt
AN : \({f_2} = 0,2\) m0,25 pt
3.1 Représentation du dispositif 1,25pt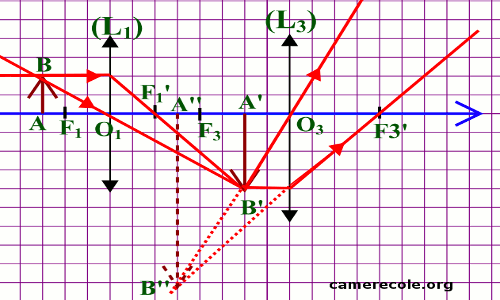
3.2 Construction de l’image A ”B’’ donnée par le système de deux lentilles 1 pt
voir image plus haut
Partie 2 : L’œil réduit
1. Identification des parties et rôles
| Symbole | Nom | Rôle |
| X | Rétine | Écran: Reçoit et convertit la lumière en influx nerveux |
| Y | Iris | Diaphragme : Permet de régler la quantité de lumière que pénètre dans l’œil |
| Z | Cristallin | Lentille convergente : permet la formation des objets observés sur la rétine |
2. L’œil met au point des objets à différentes distances en modifiant la distance focale du cristallin 0,5 pt
Partie 3 Le microscope 1,5pt
1. Puissance intrinsèque du microscope
\({P_i} = 4{G_C}\)
\({P_i} = 200\) dioptries
2. Distance focale f2 de l’oculaire
\({P_i} = \frac{{{\Delta ^2}}}{{{f_1} \times {f_2}}}\) \( = \frac{{\Delta \times {C_1}}}{{{f_2}}}\) 0,5pt
\({f_2} = \frac{{\Delta \times {C_1}}}{{{P_i}}}\) 0,5 pt
\({f_2} = 0,05\) m 0,5pt
Exercice 3 : Energie électrique 7 pts
Partie 1 : Batterie, générateur récepteur 3,75 pts
1.1 Resistance de la lampe
\(P = UI = \) \(\frac{{{U^2}}}{R} \Rightarrow \) \(R = \frac{{{U^2}}}{P}\)0,5pt
AN : \(R = 24\Omega \)0,5 pt
1.2 Intensité du courant 0,5pt
\(I = \frac{E}{R} = 0,5A\)
1.2 Durée de fonctionnement de la lampe
\(Q = I \times t\) \( \Rightarrow \) \(t = \frac{Q}{I}\)
AN : \(t = 80\) heures
2.1 Intensité I’ du courant électrique
\(U' = \) \(E' + RI'\) \( \Rightarrow \) \(I' = \) \(\frac{{U' - E'}}{R}\)
AN : \(I' = 2A\)
2.2 Diagrammes des puissances du dispositif de charge 0,75 pt
Partie 2 : Force électromotrice sinusoïdale 3,25 pts
1. Expression littérale du flux d’induction
Soit \(\overrightarrow n \) le vecteur normal à la surface de la bobine
\(\Phi (t) = \) \(N\overrightarrow B .\overrightarrow S = \) \(NBS\) \(\cos (\widehat {\overrightarrow B ,\overrightarrow n })\)0,25pt
Avec \(\theta = \widehat {\overrightarrow B ,\overrightarrow n }\) soit \(\theta = \omega t\)
\(\Phi (t) = \) \(NBS\cos (\omega t)\)0,5pt
2. Force électromotrice induite e(t)
\(e = - \frac{{d\Phi (t)}}{{dt}}\) 0,5pt
\(e = \) \(NBS\omega \) \(\sin (\omega t)\) 0,25 pt
3.1 Expression de la vitesse angulaire
\({e_{\max }}\) est obtenu de la vitesse angulaire pour \(\sin (\omega t) = 1\)
Il vient que :
\({e_{\max }} = \) \(NBS\omega \) \( \Rightarrow \) \(\omega = \) \(\frac{{{e_{\max }}}}{{NBS}}\)0,5 pt
3.2 Expression du nombre N de spires
\(\omega = 2\pi f\) \( = \frac{{{e_{\max }}}}{{NBS}}\)
\(N = \frac{{{e_{\max }}}}{{2\pi f.BS}}\)0,5 pt
3.3 Expresson numerique de N et \(\omega \)
\(B = \) \(4,6 \times {10^{ - 3}}T\), \(S = 0,01\) mm2, \({e_{\max }} = 4V\), \(f = 125Hz\)
On obtient alors :
\(N = 111\) spires 0,25pt
\(\omega = 783,4\) rad/s 0,25 pt
