Il est souhaitable de disposer d'une méthode efficace pour dénombrer les différentes situations pouvant se présenter lors d'une expérience. En fait, bien des problèmes en théorie des probabilités peuvent être résolus simplement en comptant le nombre de manières différentes selon lesquelles un certain évènement peut se réaliser. 
L’analyse combinatoire
C’est la théorie mathématique du dénombrement.
I. Le dénombrement
Le dénombrement
C’est le calcul du nombre de résultats de l'univers des résultats possibles lors d'une expérience aléatoire à plusieurs étapes.
Il convient de disposer d'une méthode efficace pour dénombrer les différentes situations pouvant se présenter lors d'une expérience.
Le dénombrement met en œuvre cinq principes décrits par Gelman et Gallistel (1978).
• Principe d’ordre stable : les mots/nombres sont toujours récités dans le même ordre;
• Principe de correspondance terme à terme : à chaque objet pointé correspond un mot/nombre et un seul;
• Principe de cardinalité : une collection d’objets est le nombre d’éléments que contient cette collection;
• Principe d’abstraction : le cardinal de la collection est indépendant de la nature des objets dénombrés;
• Principe de non-pertinence de l’ordre : l’ordre dans lequel on dénombre les objets ne change pas leur cardinal.
Deux évènements sont dits indépendants lorsque l’issue de l’un ne change pas le nombre d’issues possibles de l’autre.
Principe fondamental généralisé de dénombrement
Pour deux évènements indépendants \(?\) et \(?\) tels que le nombre d’issues possibles de l’évènement \(?\) est \(m\) et le nombre d’issues possibles de l’évènement \(?\) est \(m\), le nombre total d’issues distinctes possibles de ces deux évènements réunis est le produit \(m \times n\).
En d’autres termes : Si une expérience peut produire \(m\) résultats et une autre \(n\), alors il y a \(m \times n\) résultats possibles lorsqu'on considère ces deux expériences ensemble.
Exercice d’application
Une petite communauté se compose de dix hommes et de leurs fils, chaque homme ayant trois fils. Si un homme et l'un de ses fils doivent être désignés «père et fils exemplaires», combien y a-t-il de choix différents possibles?
Énoncé du principe fondamental généralisé de dénombrement:
Soient \({A_1}\), \({A_2}\), …, \({A_n}\) des évènements indépendants deux à deux tels que le nombre d’issues possibles de l’évènement \({A_i}\) est \({x_i}\) pour tout \(i \in {N^*}\). Le nombre total d’issues possibles distinctes de ces évènements réunis est alors égal au produit \({x_1} \times {x_2} \times ... \times {x_n}\).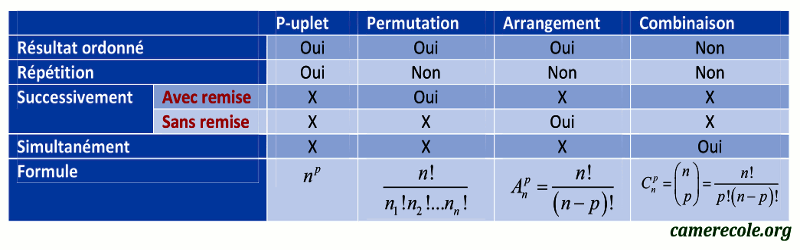
II Les permutations
En mathématiques, la notion de permutation exprime l'idée de réarrangement d'objets discernables et distinguables.
a) Permutations sans remise ou arrangement
Une permutation avec répétition de \(r\) objets pris parmi \(n\) est une suite ordonnée de \(r\) éléments choisis parmi \(n\), et pouvant se répéter.
Exemple :
Un mot de six lettres est une permutation avec répétition de six lettres choisis parmi un ensemble, l’alphabet, de 26 lettres : aaaaaa poupou, habile, garage …
Il existera alors \({26^6}\) groupes de 6 lettres pris dans 26 lettres.
La permutation peut être représentée par les \(r\) objets rangés dans des cases numérotées de \(1\) à \(r\). Pour chacune de ces \(r\) cases, il y a \(n\) choix possibles de l’objet à ranger, donc le nombre total de ces permutations est : \({n^r}\).
b) Permutations avec remise
Soit à déterminer le nombre de permutation différents qu’on peut former avec les lettres du mot « REPETER »
• Pour cela, nous avons au total \(n=7\) lettres,
• La lettre « R » est répété \({n_1} = 2\) fois ;
• La lettre « E » est répété \({n_2} = 3\) fois ;
• La lettre « P » \({n_3} = 1\) fois et la lettre « T » \({n_4} = 1\).
Ce nombre de permutation est donnée par la relation : \(\frac{{n!}}{{{n_1}!.{n_2}!{n_3}!.{n_4}!}}\)
Soit \(\frac{{7!}}{{2!.3!1!.1!}} = 420\) mots que l'on peut écrire avec les lettres du mot « REPETER »
Théorème :
Il y a \(\frac{{n!}}{{{n_1}! \times {n_2} \times ... \times {n_r}}}\) permutations différentes de n objets parmi lesquels \({{n_1}}\)sont distinguables entre eux, \({{n_2}}\) autres entre eux également, ..., \({{n_r}}\)entre eux.
Avec \(1 \le r \le n\)
NB : si \({{n_1} = {n_2} = ... = {n_r} = 1}\) alors, nous retrouvons le cas de permutation d'objets distinguables : \(n! = n(n - 1)\) \((n - 2)...0!\)
III. Les arrangements
Une permutation sans répétition, ou arrangement, de \(r\) objets pris parmi \(n\) est une suite ordonnée de \(r\) éléments choisis parmi \(n\), et qui ne peuvent pas se répéter.
Une telle permutation peut être représentée par les \(r\) objets rangés dans des cases numérotées de \(1\) à \(r\). Pour la première case il y a n choix possibles, pour la deuxième il n’y en a plus que \(n – 1\), et pour la r-ème il n’en reste plus que \(n – r + 1\); le nombre d’arrangements est donc :
\[\color{green}{A_n^r = {{n!} \over {(n - r)!}}}\]
\(A_n^r = n(n - 1)\) \(...(n - r + 1)\)
IV Les combinaisons
On est souvent appelé à déterminer le nombre de groupes de \(r\) objets qu'il est possible de former sans répétition à partir d'un total de \(n\) objets.
Une combinaison de \(r\) objets pris parmi \(n\) est tout sous-ensemble de \(r\) objets choisis sans répétition dans un ensemble en contenant \(n\).
L'expression \(\left( \begin{array}{l} n\\ r \end{array} \right)\) ou \(C_n^r\) pour \(r \le n\), est appelé combinaison de \(r\) dans \(n\) et est définie par :
\(\left( \begin{array}{l} n\\ r \end{array} \right) = C_n^r = \) \(\frac{{n!}}{{\left( {n - r} \right)!r!}}\)
\(\left( \begin{array}{l} n\\ r \end{array} \right)\) est le nombre de combinaisons de \(r\) objets pris parmi \(n\), ou encore le nombre de groupes de taille \(r\) si, dans le choix, l'ordre n'est pas considéré comme significatif.
Notons que \(\left( \begin{array}{l} n\\ r \end{array} \right) = \left( \begin{array}{l} n - 1\\ r – 1 \end{array} \right) + \) \(\left( \begin{array}{l} n - 1\\ r \end{array} \right)\)
Avec \(1 \le r \le n\)


