Correction exercice I
a) Théorème de Rolle
Soit \(f\) une fonction satisfaisant les trois conditions suivantes :
• \(f\) est continue en tout point de l’intervalle fermé [a, b] ;
• \(f\) est dérivable en tout point de l’intervalle ouvert ]a, b[ ;
• \(f(a) = f(b)\).
Alors, il existe au moins un nombre \(c\) dans ]a, b[ tel que \(f'(c) = 0\)
b) Vérifions qu'entre les racines de la fonction \(y = \) \(\sqrt[3]{{{x^2} - 5x + 6}}\) se trouve une racine de sa dérivée.
Les racines de \(y = 0\) sont : \(y = 0\) \( \Rightarrow \left\{ \begin{array}{l}x = 3\\x = 2\end{array} \right.\)
Ainsi
• \(f\) est continue en tout point de l’intervalle fermé \(\left[ {2,3} \right]\);
• \(f\) est dérivable en tout point de l’intervalle ouvert \(\left] {2,3} \right[\);
• \(f(2) = \) \(f(3) = 0\)
Alors, il existe au moins un nombre \(c\) dans \(\left] {2,3} \right[\) tel que \(f'(c) = 0\)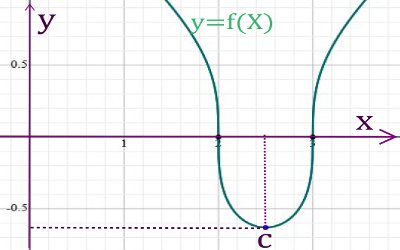
\(f'(x) = \) \(\frac{{2x - 5}}{{3{{\left( {{x^2} - 5x + 6} \right)}^{\frac{2}{5}}}}}\) avec \(x \ne 2\) et \(x \ne 3\)
\(f'(c) = 0\) \( \Rightarrow 2c - \) \(5 = 0\) soit \(c = 2,5\) qui est évidemment compris entre \(\left[ {2,3} \right]\);
b) Vérifier le théorème de Rolle pour la fonction \(y = {\cos ^2}x\) sur le segment \(\left[ { - \frac{\pi }{4},\frac{\pi }{4}} \right]\)
• \(f\) est continue en tout point de l’intervalle fermé \(\left[ { - \frac{\pi }{4},\frac{\pi }{4}} \right]\) ;
• \(f\) est dérivable en tout point de l’intervalle ouvert \(\left] { - \frac{\pi }{4},\frac{\pi }{4}} \right[\);
• \(f\left( { - \frac{\pi }{4}} \right) = \) \({\cos ^2}\left( { - \frac{\pi }{4}} \right) = \) \({\cos ^2}\left( {\frac{\pi }{4}} \right) = \) \(f\left( {\frac{\pi }{4}} \right) = \frac{1}{2}\)
Alors, il existe au moins un nombre \(c\) dans \(\left[ { - \frac{\pi }{4},\frac{\pi }{4}} \right]\) tel que \(f'(c) = 0\)
\(f'(x) = \) \( - 2\cos x\sin x\) \( = - \sin 2x\) \( = 0\)
\(f'(c) = \) \( - \sin 2c = \) \(0 \Rightarrow \) \(\left\{ \begin{array}{l}x = \pi n\\x = \frac{\pi }{2} + n\pi \end{array} \right.\) avec \(n \in \mathbb{Z}\)
Pour \(n = 0\), on \(c = 0 \in \) \(\left] { - \frac{\pi }{4},\frac{\pi }{4}} \right[\)
Correction exercice II
1. Énonçons le théorème des accroissements finis (théorème de Lagrange)
Soit \(f\) une fonction vérifiant les deux conditions suivantes :
• \(f\) est continue en tout point de \(\left[ {a,b} \right]\) ;
• \(f\) est dérivable en tout point de \(\left] {a,b} \right[\) ;
Alors, il existe au moins un nombre \(c\) dans l’intervalle \(\left] {a,b} \right[\) tel que : \(f'(c) = \) \(\frac{{f(b) - f(a)}}{{b - a}}\)
C'est-à-dire \(f(b) - f(a)\) \( = f'(c)(b - a)\)
2. Déterminons parmi les fonctions suivantes lesquelles satisfont les conditions de théorème des accroissements finis sur I
a) \(f(x) = {x^2}\) sur \(I = \left[ {0,3} \right]\)
la fonction \(f(x)\) est continue sur \(0 \le x \le 3\) et dérivable sur \(0 \prec x \prec 3\) de plus \(f(0) \le f(x)\) \( \le f(3) \Leftrightarrow \) \(0 \prec f(x) \prec 9\). Selon le théorème des accroissements finis, il doit exister un point \(c\) de l’intervalle de définition pour lequel \(f'(x) = 2x\) est égale aussi à \(\frac{{f(3) - f(0)}}{{3 - 0}}\) \( = \frac{{9 - 0}}{{3 - 0}} = 3\)
ainsi \(f'(c) = 3\) \( \Rightarrow c = \frac{3}{2}\)
il existe alors un point \(C\left( \begin{array}{l}\frac{3}{2}\\\frac{9}{4}\end{array} \right)\)entre \(A\left( \begin{array}{l}0\\0\end{array} \right)\) et \(B\left( \begin{array}{l}3\\9\end{array} \right)\) tel que la tangente en ce point est parallèle à la corde AB.
b) Exactement comme précédemment.
