Définition

Soit \(y = f(x)\) une fonction croissante (décroissante) définie dans l'intervalle \(\left[ {a,b} \right]\) avec \(a \prec b\). Soient \(f(a) = c\), \(f(b) = d\). En considérant la valeur de y comme la valeur de la variable indépendante et les valeurs de x comme les valeurs de la fonction, nous obtenons x en fonction de y : \(x = \varphi (y)\)
Cette fonction est appelée fonction inverse de la fonction \(y = f(x)\).
Si la fonction croissante (ou décroissante) \(y = f(x)\) est continue sur le segment \(\left[ {a,b} \right]\) et \(f(a) = c\), \(f(b) = d\) alors la fonction inverse est définie et continue sur le segment \(\left[ {c,d} \right]\).
Si la fonction \(y = f(x)\) admet une fonction inverse \(x = \varphi (y)\) dont la dérivée \(\varphi '(y)\) en un point donné est différente de zéro, alors la fonction \(y = f(x)\) possède au point x correspondant une dérivée \(f'(x)\) égale à \(\frac{1}{{\varphi '(y)}}\), c'est-à-dire que nous avons la formule :
\(f'(x) = \frac{1}{{\varphi '(y)}}\)

Démonstration :
\(x = \varphi (y) \Rightarrow \) \(\frac{d}{{dx}}x = \frac{{d\varphi (y)}}{{dx}}\) \( = \frac{{d\varphi (y)}}{{dy}}\frac{{dy}}{{dx}}\) \( = {\varphi _y}'(y).y{'_x}\)
\(1 = {\varphi _y}'(y).y{'_x}\) \( = {\varphi _y}'(y).f'(x)\)

II. Fonctions trigonométriques inverses et leurs dérivées

Considérons la \(y = \sin x\) dont la réciproque est \(x = \sin y\) et traçons son graphique en prenant pour axe Oy la verticale ascendante avec \( - \frac{\pi }{2} \le y \le \frac{\pi }{2}\) et \( - 1 \le x \le 1\)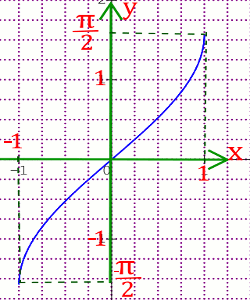
La dérivée de la fonction \(\arcsin x\) est \(\frac{1}{{\sqrt {1 - {x^2}} }}\)
En effet,
\(x = \sin y \Rightarrow \) \(\frac{{dx}}{{dx}} = 1 = \) \(\frac{{d\sin y}}{{dy}}.\frac{{dy}}{{dx}} = \) \(\cos y.y{'_x}\)
\(y{'_x} = \frac{1}{{\cos y}} = \) \(\frac{1}{{\sqrt {1 - {{\sin }^2}y} }} = \) \(\frac{1}{{\sqrt {1 - {x^2}} }} = \) \((\arcsin x)'\)

\((\arcsin x)' = \frac{1}{{\sqrt {1 - {x^2}} }}\)

De la même façon, on montre que : \((\arccos x)' = - \frac{1}{{\sqrt {1 - {x^2}} }}\), \((\arctan x)' = \frac{1}{{1 + {x^2}}}\) et \(({\mathop{\rm arccot}\nolimits} anx)' = \) \( - \frac{1}{{1 + {x^2}}}\)

On montre que :

\(\arccos x + \) \(\arcsin x = \frac{\pi }{2}\)

\(\arctan x + \) \(\arctan y = \) \(\arctan \frac{{x + y}}{{1 - xy}} + \) \(n\pi \)
\(n = 0\) si \(xy \prec 1\)
\(n = + 1\) si \(xy \succ 1\) avec \(x\) et \(y\) positifs
\(n = - 1\) si \(xy \succ 1\) avec \(x\) et \(y\) négatifs

\(\arctan x + \) \({\mathop{\rm arccot}\nolimits} anx = \frac{\pi }{2}\)

\({\mathop{\rm arccot}\nolimits} anx = \) \(\arctan \frac{1}{x}\) si \(x \succ 0\)

\({\mathop{\rm arccot}\nolimits} anx = \) \(\pi + \arctan \frac{1}{x}\) si \(x \prec 0\)

\(\tan (x + y) = \) \(\frac{{\tan x + \tan y}}{{1 + \tan x.\tan y}}\)

\(\tan (x - y) = \) \(\frac{{\tan x \tan y}}{{1 + \tan x.\tan y}}\)

Expression de \(\sin x\), \(\cos x\) et \({\tan x}\) en fonction de \(\tan \frac{x}{2} = t\)

\(\sin x = \frac{{2t}}{{1 + {t^2}}}\)

\(\cos x = \frac{{1 - {t^2}}}{{1 + {t^2}}}\)

\(\tan x = \frac{{2t}}{{1 - {t^2}}}\)